Презентация по математике "Производная. Применение производной"

Цель:

Систематизировать ранее расcмотренный материал.

Знания и навыки учащихся

Знать производные элементарных функций и правила дифференцирования.

Знать признак возрастания (убывания) функции.

Уметь составлять уравнение касательной к графику функции.

Знать определение  критических точек, точек максимума (минимума) функции .

Знать алгоритм исследования и построения графика функции с помощью производной.

Уметь применять полученные сведения для построения графиков функций на основе предварительного проведённого исследования функции в соответствии с планом.

Готовится  к  ЕГЭ.

Проверка домашнего задания                                                                                     

1. Задание №8 (ЕГЭ).           

Найдите наименьшее значение функции на отрезке 5;7                                                                                                      

2. № 5.64 (в)  

Точка движется по прямой по закону. Определите скорость и ускорение в момент времени.                                                                                     

3. Написать уравнение касательной к графику функции  у=    в точке х =     .

4.  №5.32 (а)  

Под каким углом пересекает ось Ох график функции у=   в каждой  из точек пересечения.

5.  (ЕГЭ  2009 част С1)

Найдите абсциссу точки графика функции у=   , касательная в которой параллельна прямой у=    .

Дополнительно. Построить график функции у=     , можно с презентацией.

Найдите область определения функции.

Экстремумы функции

Наибольшее значение функции на отрезке называют максимумом функции на отрезке.

Наименьшее значение функции на отрезке называют минимумом функции на отрезке.

Точки максимума и минимума  называют точками экстремума. 

Если хо - точка экстремума дифференцируемой функции  f(x), то

f  /(xо)=0.

Точки, в которых функция имеет производную, равную нулю, или недифференцируема, называют критическими точками этой функции.

Пусть функция f(x) дифференцируема на интервале (а;в), хо ∈ (а;в), и f /(х)=0.

Тогда:

1) если при переходе через критическую точку хо функции f(x) её производная меняет знак с "+" на "-", т.е. f /(x)>0 слева от хо и  f /(x)<0 справа от точки хо, то хо - точка максимума функции f(x);

2) если при переходе через стационарную точку хо функции f(x) её производная меняет знак с "-" на "+", т.е., f /(x)<0 слева от хо и  f /(x)>0 справа от точки хо, то хо - точка минимума функции f(x).

План исследования и построения графика функции с помощью производной

1.Найти область определения функции.

2. Найти производную функции.                                                                              

3. Определить является ли функция чётной или является нечётной.

4. Найти точки экстремума.

5. Найти промежутки возрастания и убывания функции.

6. Результаты исследования записать в виде таблицы. Найти несколько дополнительных точек графика функции. Построить график функции.

Итог урока

Задания ученикам по рефлексии их деятельности.

Цель: воспроизвести динамику чувств и ощущений учащихся за время участия в уроке.

- Какие вопросы по изучаемой теме тебе стали более понятны?

- Что осталось неясным по изучаемым темам?

- Удовлетворен ли ты своей оценкой, полученной на этом уроке?

- Как оценил бы ты себя сам?

- Как часто тебе хотелось ответить на вопрос учителя?

- Нравится ли тебе работать у доски?

Теория без практики мертва или бесплодна, практика без теории невозможна или пагубна.

Для теории нужны знания, для практики, сверх всего того, и умение.

А.Н. Крылов

Производная. Применение производной.

11 класс. Учитель: Коленкова Людмила Николаевна

Тема урока: « Производная и её применение». Тип урока: Урок закрепления и совершенствование знаний.

• - организационный момент ; - постановка цели;
• - проверка домашнего задания;
• - воспроизведение ранее полученных знаний;
• - свобода деятельности в новой ситуации;
• - контроль усвоения полученных знаний;
• - домашнее задание и его инструктаж - подведение итогов урока.

13.12.10.

Цель. Систематизировать ранее расcмотренный материал .

Знания и навыки учащихся.

• Знать производные элементарных функций и правила дифференцирования.
• Знать признак возрастания (убывания) функции.
• Уметь составлять уравнение касательной к графику функции.
• Знать определение критических точек, точек максимума (минимума) функции .
• Знать алгоритм исследования и построения графика функции с помощью производной.
• Уметь применять полученные сведения для построения графиков функций на основе предварительного проведённого исследования функции в соответствии с планом. Готовится к ЕГЭ.

Проверка домашнего задания.

1. Задание №8 ( ЕГЭ ). Найдите наименьшее значение функции на отрезке 5;7

2. № 5.64 (в) Точка движется по прямой по закону .Определите скорость и ускорение в момент времени .

3. Написать уравнение касательной к графику функции у= в точке х =

4. №5.32 (а) Под каким углом пересекает ось Ох график функции у= в каждой из точек пересечения . У=

5. ( ЕГЭ 2009 част С1 ) Найдите абсциссу точки графика функции у= , касательная в которой параллельна прямой у=

Дополнительно . Построить график функции у= можно с презентацией

R, кроме 0

(действительные числа)

x ∈ (5;+ ∞ )

у = х 3 -2х 2 +3

Область определения

Функция

R

(действительные числа)

x ∈ (- ∞;-5]

у = х 3 -2х 2 +3

R

(действительные числа)

x ∈ [5;+ ∞ )

у = 1-2,5х 2 -х 5

у = 1/(х+2)

1. Найдите область определения функции.

R

(действительные числа)

у = 1+2/х

у = х - sin2x

R

(действительные числа)

у = 1+3 √x-5

R

(действительные числа)

у = xe x

R, кроме π /2+ π n,

n ∈ Z

у = tgх -2

R , кроме -2

(действительные числа)

R

(действительные числа)

2. Установите соответствие функция-производная.

Функция

Производная

у = х 3 -2х 2 +3

у / = 1- 2cos2x

у = 1-2,5х 2 -х 5

у / = -5х-5х 4

у = 1/(х+2)

у / = 3/2 √x-5

у / = 1/cos 2 х

у = 1+2/х

у / = -2/х 2

у = х - sin2x

у / = e x (1+x)

у = 1+3 √x-5

у / = 3х 2 -4х

у = xe x

у = tgх -2

у / = - 1/(х+2) 2

Решение задач по теме : «Применение производной к решению задач, к построению графиков функций.

• 1.( ЕГЭ 2009), часть С1. Найдите абсциссы всех точек графика функции

касательные в которых параллельны прямой у= или совпадают с ней. 2.№ 5.59. Доказать, что функция на отрезке -1;3 емеет один корень.

3.

Экстремумы функции

• Наибольшее значение функции на отрезке называют максимумом функции на отрезке.
• Наименьшее значение функции на отрезке называют минимумом функции на отрезке

• Точки максимума и минимума называют тачками экстремума.

0 слева от х о и f / (x) о , то х о - точка максимума функции f(x); 2)если при переходе через стационарную точку х о функции f(x) её производная меняет знак с "-" на "+", т.е., f / (x) о и f / (x)0 справа от точки х о , то х о - точка минимума функции f(x). " width="640"

Если х о - точка экстремума дифференцируемой функции f(x), то

f / (x о )=0.

• Точки, в которых функция имеет производную, равную нулю, или недифференцируема, называют критическими точками этой функции.
• Теорема.

Пусть функция f(x) дифференцируема на интервале (а;в), х о ∈ (а;в), и

f / (х)=0.

Тогда:

1)если при переходе через критическую точку х о функции f(x) её производная меняет знак с "+" на "-", т.е. f / (x)0 слева от х о и f / (x) о , то х о - точка максимума функции f(x);

2)если при переходе через стационарную точку х о функции f(x) её производная меняет знак с "-" на "+", т.е., f / (x) о и f / (x)0 справа от точки х о , то х о - точка минимума функции f(x).

Применение производной к построению графиков функций.

План исследования и построения

графика функции с помощью производной.

1. Найти область определения функции.

2. Найти производную функции. 3. Определить является ли функция чётной или является нечётной.

4. Найти точки экстремума .

5. Найти промежутки возрастания и убывания функции.

6 .Результаты исследования записать в виде таблицы. Найти несколько дополнительных точек графика функции. Построить график функции.

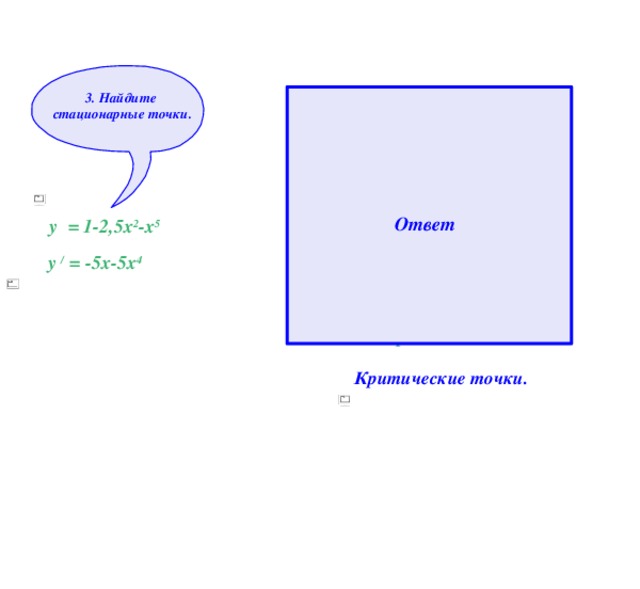
3. Найдите

стационарные точки.

у / = -5х-5х 4 , у / = 0.

-5х-5х 4 =0

-5х(1+х 3 )=0

-5х=0 или (1+х 3 )=0

х=0:(-5) х 3 =0-1

х=0 х 3 =-1

х= ∛- 1

х= -1

х 1 =0 и х 2 = -1

стационарные точки.

Ответ

у = 1-2,5х 2 -х 5

у / = -5х-5х 4

Критические точки.

0. 3.(0;+ ∞ ): f / (1)= -5(1) - 5(1) 4 = -5-5= -10, -10Функция возрастает на промежутке [-1;0]. Функция убывает на промежутке (- ∞ ; -1], [0; + ∞ ). Ответ Промежутки возрастания и убывания функции. " width="640"

26.11.2008

Классная работа.

Применение производной к построению графиков функций.

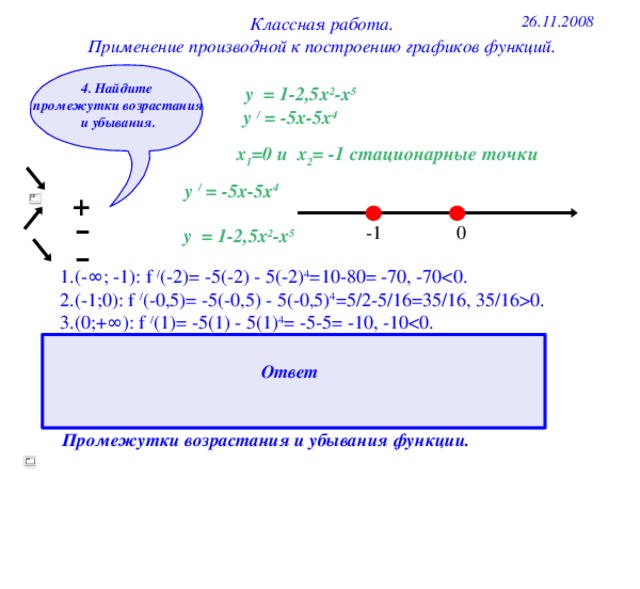
4. Найдите

промежутки возрастания и убывания.

у = 1-2,5х 2 -х 5

у / = -5х-5х 4

х 1 =0 и х 2 = -1 стационарные точки

у / = -5х-5х 4

+

-

-1

0

-

у = 1-2,5х 2 -х 5

1.(- ∞ ; -1): f / (-2)= -5(-2) - 5(-2) 4 =10-80= -70, -70

2.(-1;0): f / (-0,5)= -5(-0,5) - 5(-0,5) 4 =5/2-5/16=35/16, 35/160.

3.(0;+ ∞ ): f / (1)= -5(1) - 5(1) 4 = -5-5= -10, -10

Функция возрастает на промежутке [-1;0].

Функция убывает на промежутке (- ∞ ; -1], [0; + ∞ ).

Ответ

Промежутки возрастания и убывания функции.

26.11.2008

Классная работа.

Применение производной к построению графиков функций.

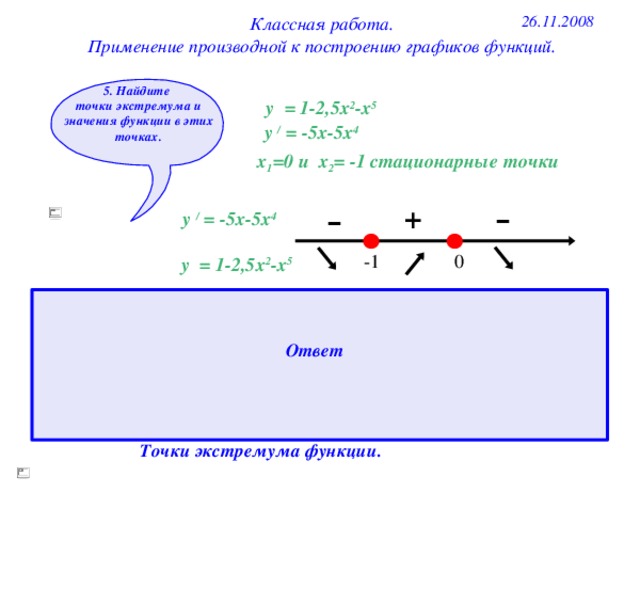
5. Найдите

точки экстремума и значения функции в этих точках.

у = 1-2,5х 2 -х 5

у / = -5х-5х 4

х 1 =0 и х 2 = -1 стационарные точки

-

-

+

у / = -5х-5х 4

0

-1

у = 1-2,5х 2 -х 5

1. При переходе через стационарную точку -1 производная меняет знак с "-" на "+", х 2 =-1 - точка минимума.

f(-1)=1-2,5(-1) 2 -(-1) 5 =1-2,5+1= -0,5.

2. При переходе через стационарную точку 0 производная меняет знак с "+" на "-", х 1 =0 - точка максимума.

f(0)=1-2,5(0) 2 -(0) 5 =1-0-0=1.

Ответ

Точки экстремума функции.

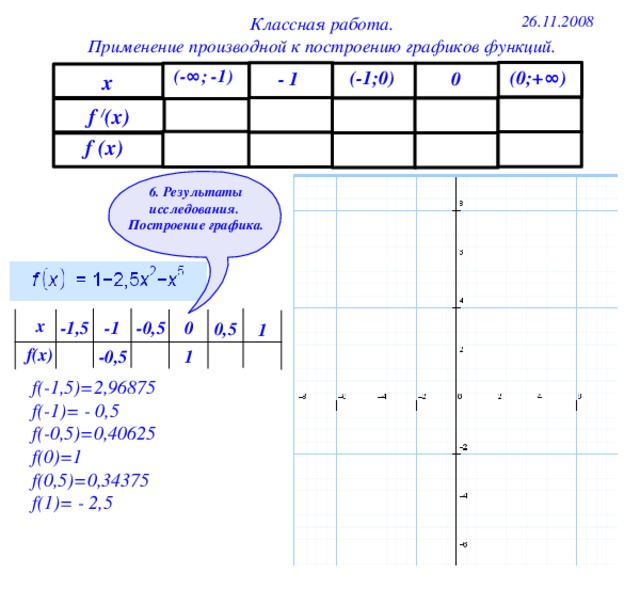
26.11.2008

Классная работа.

Применение производной к построению графиков функций.

(- ∞ ; -1)

(0;+ ∞ )

(-1;0)

- 1

0

x

f / (x)

f (x)

6. Результаты исследования.

Построение графика.

х

-1

-1,5

0

-0,5

0,5

1

f(х)

-0,5

1

f(-1,5)=2,96875

f(-1)= - 0,5

f(-0,5)=0,40625

f(0)=1

f(0,5)=0,34375

f(1)= - 2,5

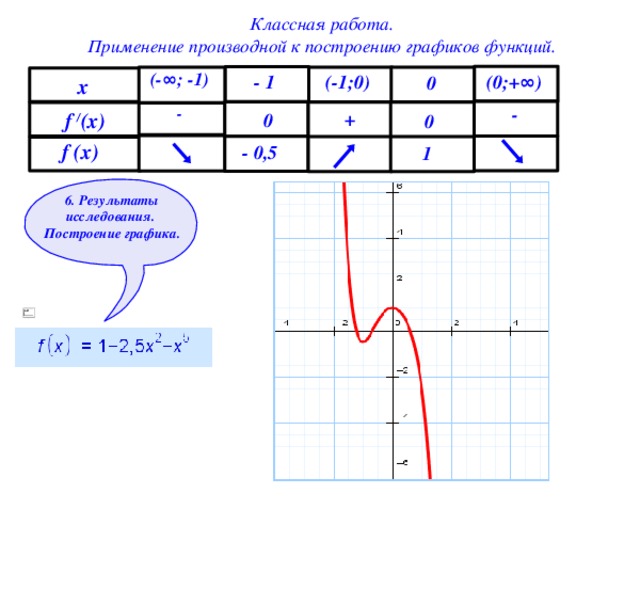
Классная работа.

Применение производной к построению графиков функций.

(- ∞ ; -1)

(0;+ ∞ )

(-1;0)

- 1

0

x

-

-

+

f / (x)

0

0

f (x)

- 0,5

1

6. Результаты исследования.

Построение графика.

Применение производной к построению графиков функций.

План исследования и построения

графика функции с помощью производной.

1. Найти область определения функции.

2. Найти производную функции. 3. Определить является ли функция чётной или является нечётной.

4. Найти точки экстремума .

5. Найти промежутки возрастания и убывания функции.

6 .Результаты исследования записать в виде таблицы. Найти несколько дополнительных точек графика функции. Построить график функции.

Применение производной к построению графиков функций.

Задания для классной работы.

Построить график функции.

1. у=х 3 -3х 2 +4 2. у= - х 3 +4х 2 -4х.

Задания для домашней работы

Применение производной к построению графиков функций.

Итог урока.

Задания ученикам по рефлексии их деятельности.

Цель. Воспроизвести динамику чувств и ощущений учащихся за время участия в уроке.

1.Какие вопросы по изучаемой теме тебе стали более понятны?

2.Чт о осталось неясным по изучаемым темам?

3. Удовлетворен ли ты своей оценкой, полученной на этом уроке?

4. Как оценил бы ты себя сам?

5. Как часто тебе хотелось ответить на вопрос учителя?

6. Нравится ли тебе работать у доски?

Производная . Применение производной .

Спасибо за урок!