Федеральное агентство морского и речного транспорта
Красноярский институт водного транСпорта - филиал
Фгбоу во «СИБИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ВОДНОГО ТРАНСПОРТА»
|
|
Методическое пособие
к изучению темы
«Уравнения и неравенства».
Разработал: преподаватель ФМЦ ПЦК
Н.В. Вервейн
2024 г.
Содержание
Введение. 3
Тема 1. Решение уравнений 1-ой и 2-ой степени (повторение). 5
Тема 2. Методы решения уравнений степени, большей 2-ой: замена переменной, разложение на множители, графический метод. 8
Тема 3. Решение иррациональных уравнений. 10
Тема 4*. Уравнения с модулем. 12
Тема 5 Решение неравенств 1-ой и 2-ой степени (повторение). 13
Тема 6 Метод интервалов. 15
Тема 7*. Решение иррациональных неравенств и неравенств с модулем. 17
Тема 8. Решение систем уравнений с двумя переменными. 19
Ответы к заданиям для самостоятельного решения 20
Домашняя контрольная работа 21
Список рекомендуемой литературы 24
Заключение. 25
Введение.
Данное учебное пособие разработано для студентов 1 курса, изучающих курс математики как на профильном, так и на базовом уровне. Целью данного пособия является организация практических аудиторных занятий по всей теме и самостоятельной работы студентов.
Весь курс разбит на 8 тем, по каждой из которых приводятся краткие теоретические сведения, примеры решения заданий и упражнения для самостоятельной работы. К каждому заданию приводиться ответ. По курсу предусмотрена домашняя контрольная работа, задания для которой приводятся в данном пособии. Все задания разбиты на два уровня: обязательный и достаточный, задания более высокого уровня сложности отмечены знаком *, этим же значком отмечены темы, которые могут не изучаться на базовом уровне.
Пояснительная записка
Учебное пособие может быть использовано как при организации аудиторной, так и внеаудиторной работы. Работа над пособием предусматривает:
1. Изучение либо повторение теоретического материала
2. Изучение разобранных примеров решения упражнений
3. Самостоятельное решение упражнений
Одновременно студент выполняет домашнюю контрольную работу, задания для которой приведены на стр. 21. Номер варианта определяется по порядковому номеру студента в списке группе: по последней цифре. Например, если студент имеет номер 17, значит его вариант № 7, и из каждого задания необходимо решить упражнение с номером 7.
При работе над темой может использоваться дополнительная учебная литература, список которой приведен на стр. 24.
Тема 1. Решение уравнений 1-ой и 2-ой степени (повторение).
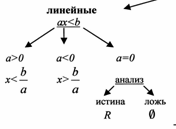
Линейное уравнение имеет вид ax = b, где a и b – числа.
В зависимости от значений a и b возможны следующие случаи решения линейных уравнений:
![]()

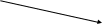
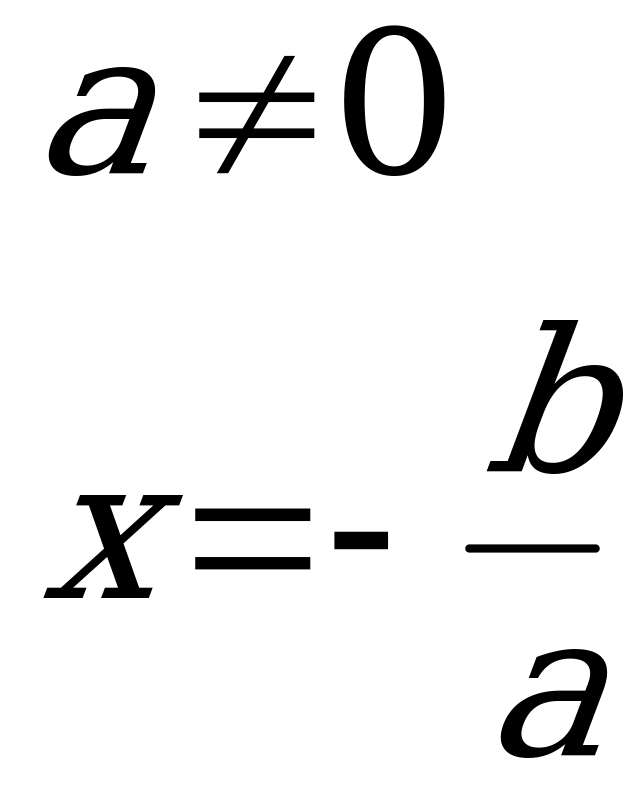
![]()
![]()
х – любое число
Пример 1. Решить уравнение ![]() .
.
С помощью раскрытия скобок и приведения подобных слагаемых это уравнение приводится к виду ах + b = 0.
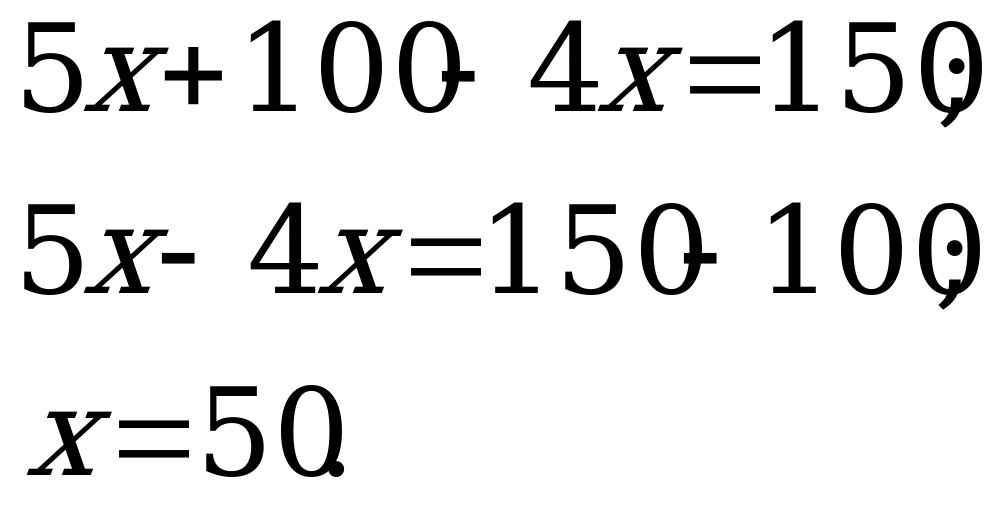
Ответ: ![]()
П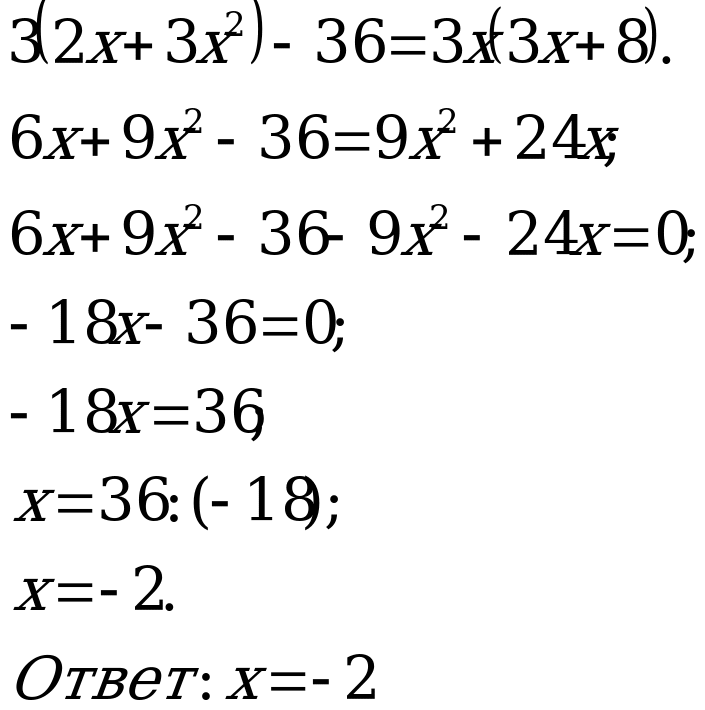 ример 2. Решить уравнение:
ример 2. Решить уравнение:
Уравнение вида ![]() , где
, где ![]() называется квадратным уравнением.
называется квадратным уравнением.
В зависимости от значений b и c уравнения делятся на полные и неполные.
Полное квадратное уравнение – то, в котором ![]() и
и ![]() .
.
Общая схема решения такого уравнения сводится к нахождению дискриминанта и отысканию корней по специальным формулам.
Схема выглядит следующим образом:
![]()
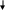
![]()
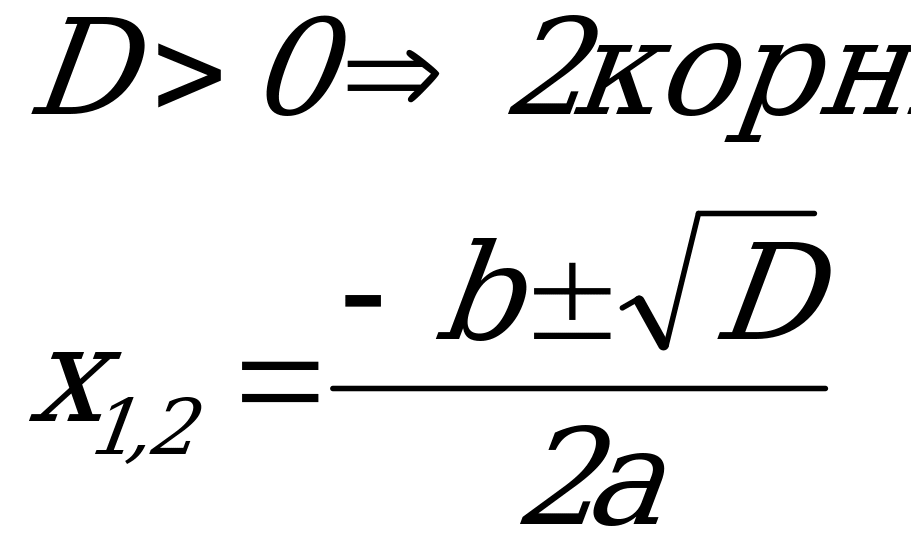
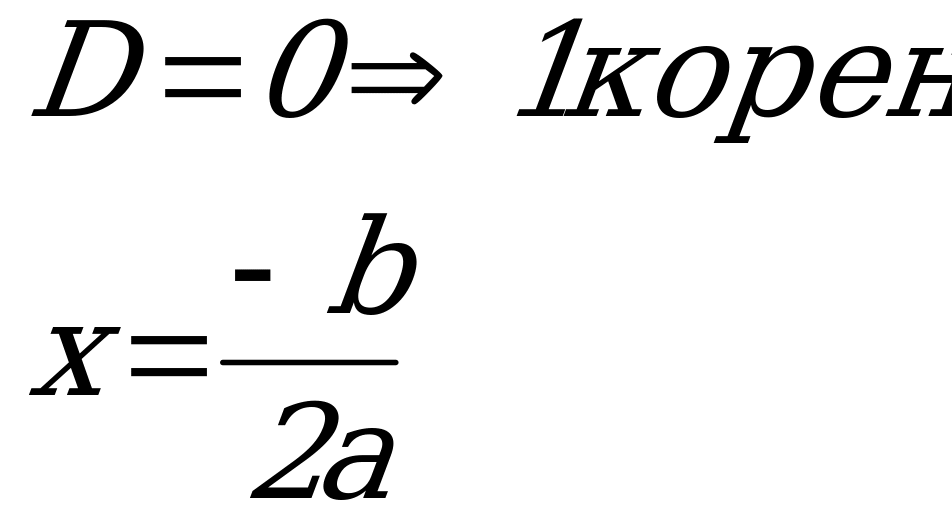
![]()
П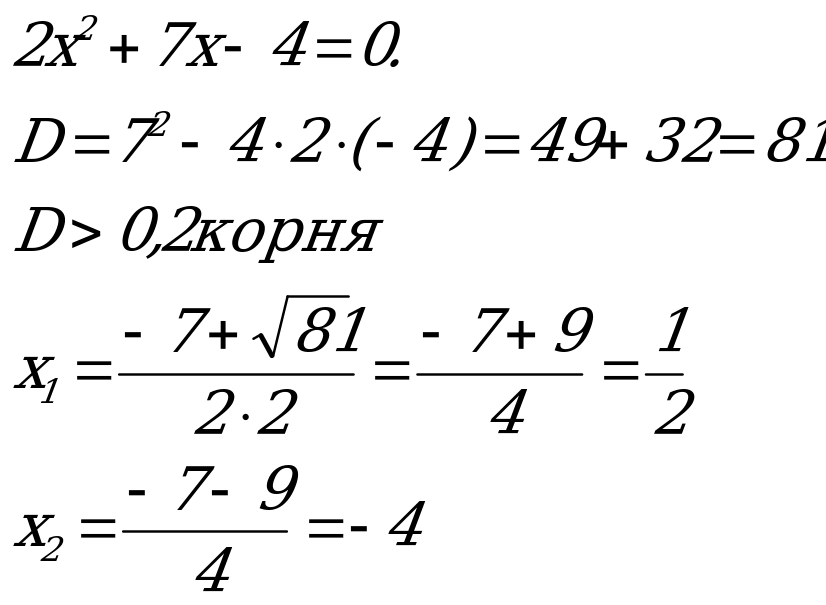 ример 3. Решить уравнение
ример 3. Решить уравнение
Пример 4. Решить уравнение: ![]()
Сначала раскроем скобки: ![]()
Так как уравнение является квадратным, то приведем его к стандартному виду. Для этого перенесем все слагаемые в левую часть. Получим:![]()
Приведем подобные слагаемые: ![]() . Теперь решаем его как полное квадратное уравнение.
. Теперь решаем его как полное квадратное уравнение.
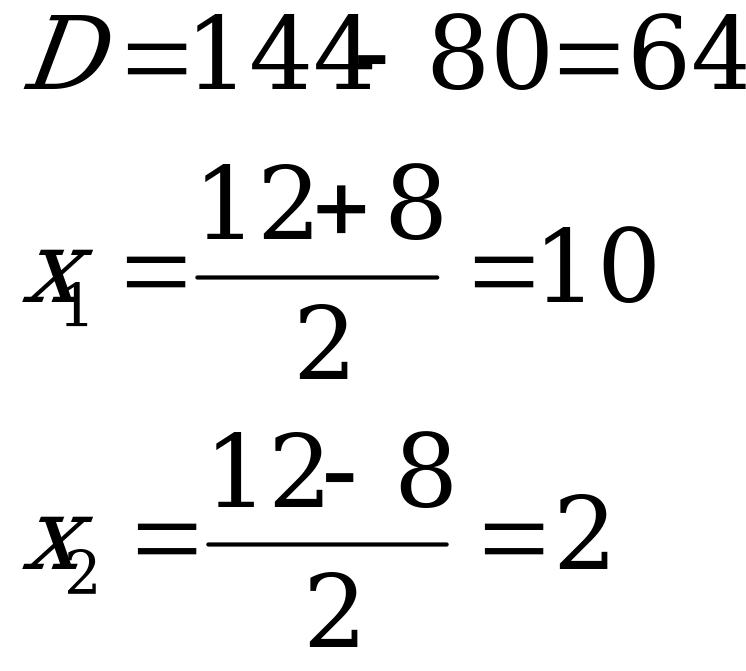
Ответ: ![]()
Неполные квадратные уравнения – уравнения, в которых b или с равны 0. Общая схема решения зависит от вида уравнения.
|
| с=0 |
|
| Таким образом, уравнение такого вида всегда имеет два корня, один из которых равен 0. |
П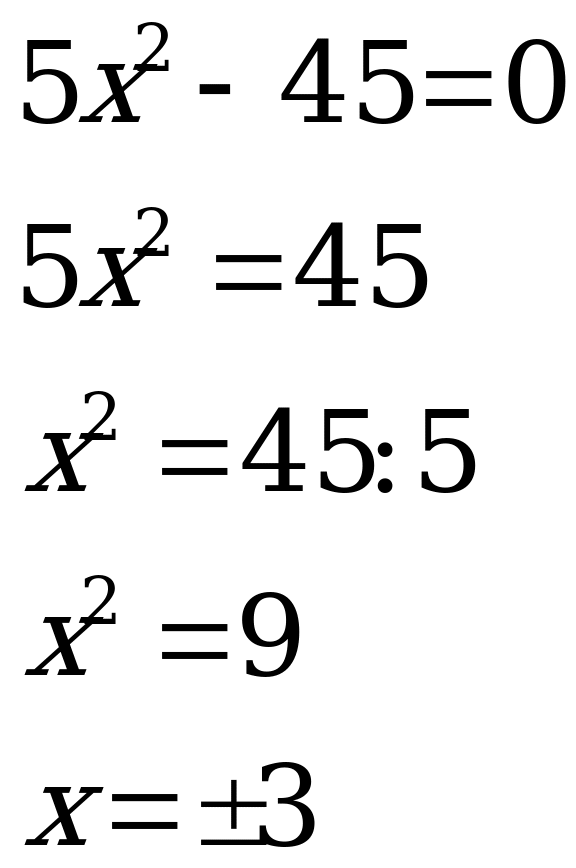 ример 5. Решить уравнение
ример 5. Решить уравнение
Ответ : ![]()
П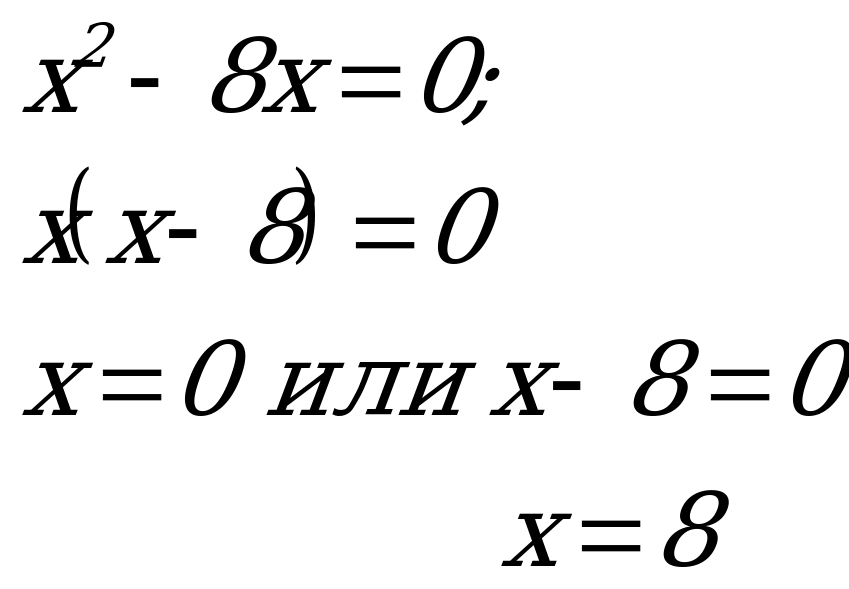 ример 6. Решить уравнение
ример 6. Решить уравнение
Ответ: ![]()
Иногда при решении уравнений более высоких степеней с помощью замены переменной можно получить уравнение второй степени. Рассмотрим примеры.
Пример 7. Решить уравнение![]()
Уравнение такого вида называется биквадратным уравнением и решается оно с помощью стандартной замены переменной.
Пусть ![]() , тогда уравнение примет вид:
, тогда уравнение примет вид: ![]()
Решим его, получим: ![]()
Теперь вернемся к замене переменной. Получим:
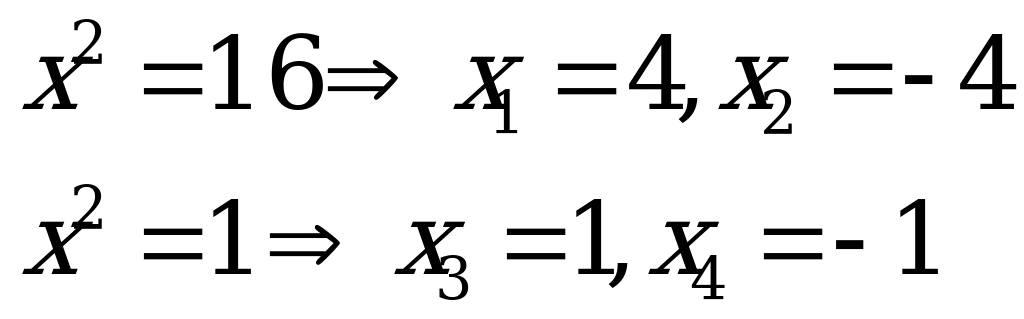
Ответ: ![]() .
.
Дробно – рациональные уравнения – уравнения, содержащие неизвестную переменную в знаменателе.
Решение таких уравнений производится по следующему алгоритму:
1. Перенести все слагаемые в левую часть уравнения
2. Привести левую часть к общему знаменателю
3. Упростить числитель
4. Приравнять числитель к 0 и решить полученное уравнение
5. Из найденных в п. 4 корней оставить только те, которые не обращают знаменатель в 0.
П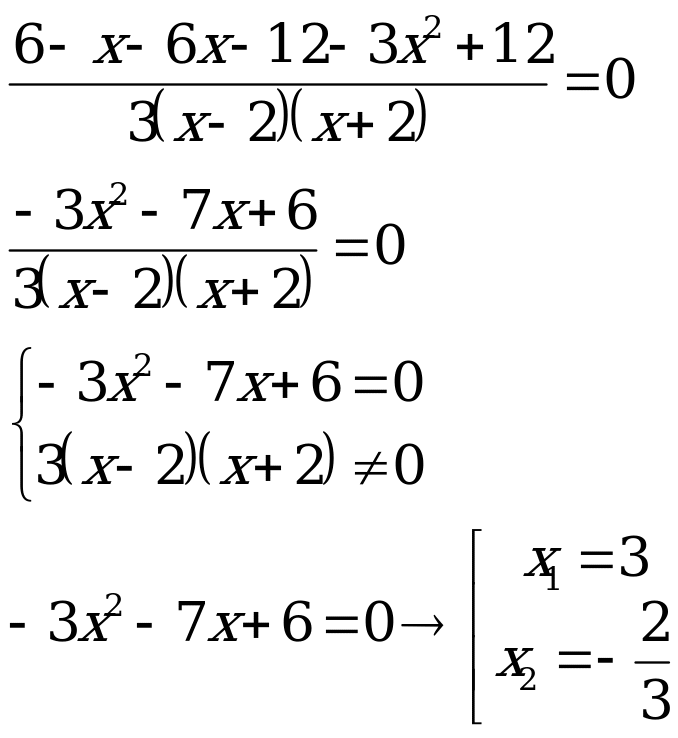 ример 8. Решить уравнение
ример 8. Решить уравнение
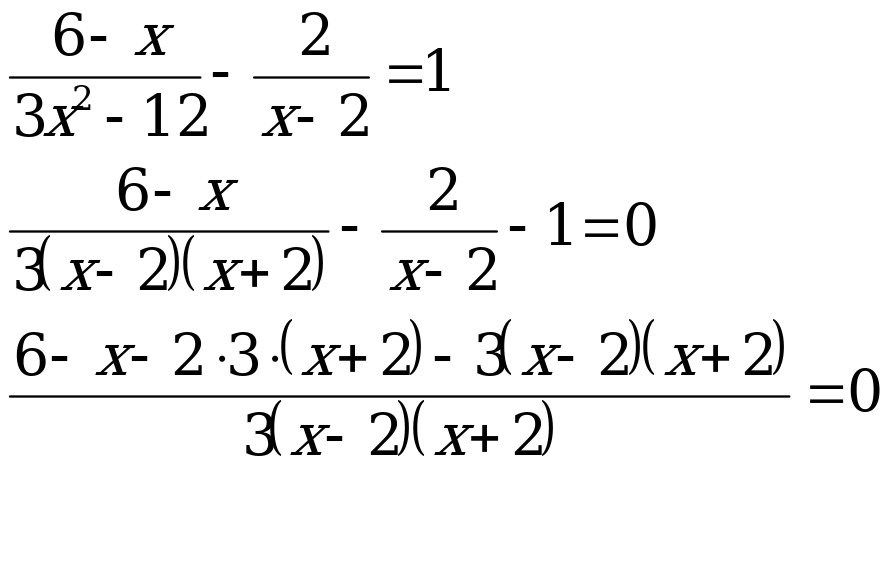
При ![]() - верно
- верно
При ![]() - верно
- верно
Ответ: ![]()
Задания для самостоятельного решения:
Обязательный уровень:
1. 5х(2х+1)=0
2. 100х2-25=0
3. х2 – 9 х + 18 =0
4. х2 +8х+12=0
5. х2 + х =0
6. 6(2 - х2) = 7(3 – х2) – 9
7. 7х(2 + х) = 5х(х – 4)
8. х4 – 25х2 + 144 = 0
9. х4 -11 х2 + 18 = 0
10. ![]()
11. ![]()
12.![]()
Достаточный уровень
13. ![]()
14. ![]()
15.![]()
Тема 2. Методы решения уравнений степени, большей 2-ой: замена переменной, разложение на множители, графический метод.
При решении уравнений степени, большей 2, применяется множество методов. Наиболее часто используемые – замена переменной и разложение на множители. Рассмотрим применение этих методов подробнее на следующих примерах.
Замена переменной. Этот метод применялся уже ранее при решении биквадратных уравнений.
Пример 1. Решить уравнение ![]()
Если попытаться в этом уравнении раскрыть скобки и привести подобные слагаемые, то получится уравнение 4 степени, но не биквадратное. Решить его стандартным способом не удается. Поэтому решим его иначе. Заметим, что уравнение имеет общую часть, обозначим ее новой переменной (в этом заключается общий шаг решения всех уравнений методом замены переменной).
Пусть ![]()
П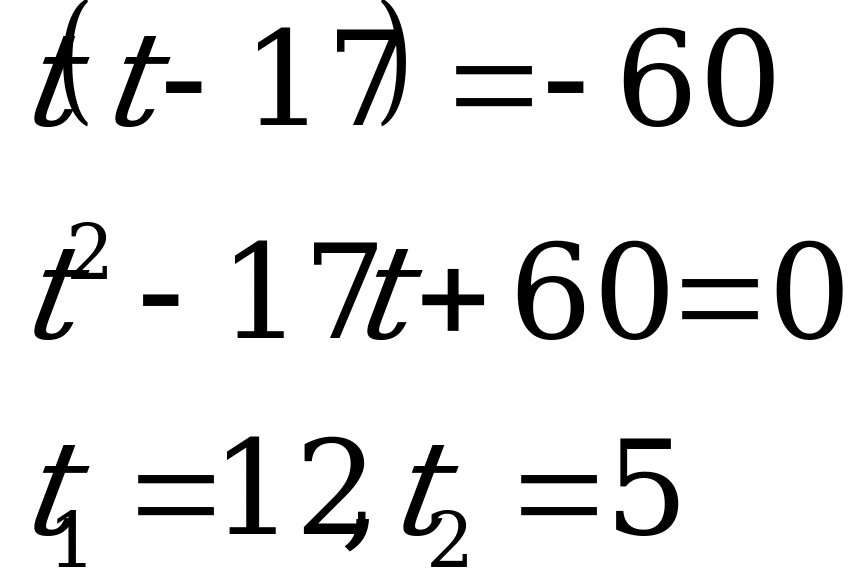 олучим
олучим
Т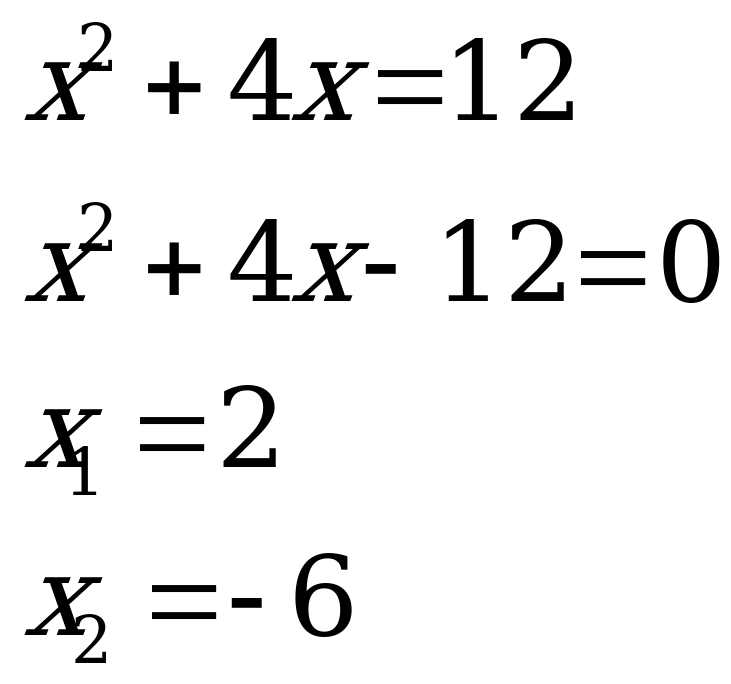 еперь вновь вернемся к замене переменной. Получим:
еперь вновь вернемся к замене переменной. Получим:
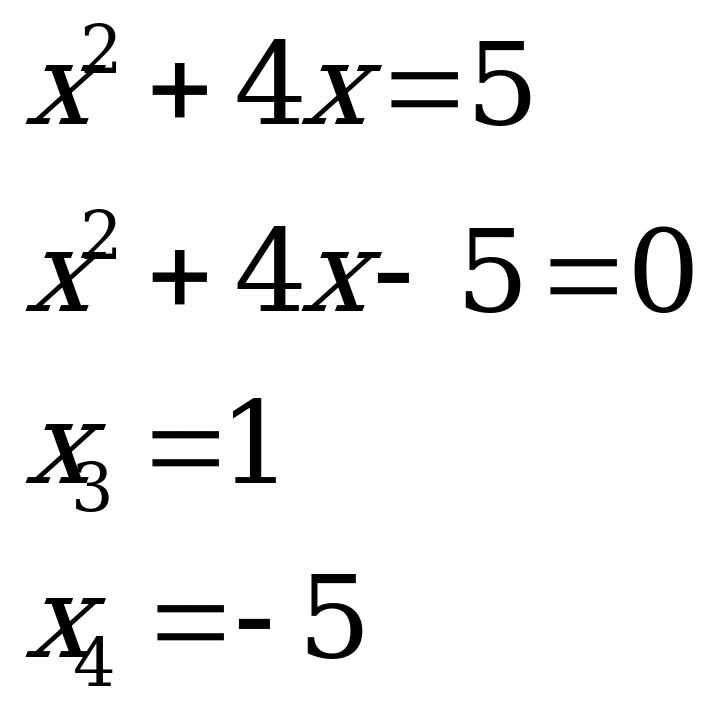
Ответ: 2; -6; 1; -5
Разложение на множители. Этот метод так же ранее применялся при решении неполных квадратных уравнений в случае, когда с = 0 (пример 6). В основе этого метода лежит утверждение: произведение равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю. При решении уравнений важно, чтобы левая часть была разложена на множители, а правая была равна нулю. Схема метода выглядит следующим образом:
![]()
![]()
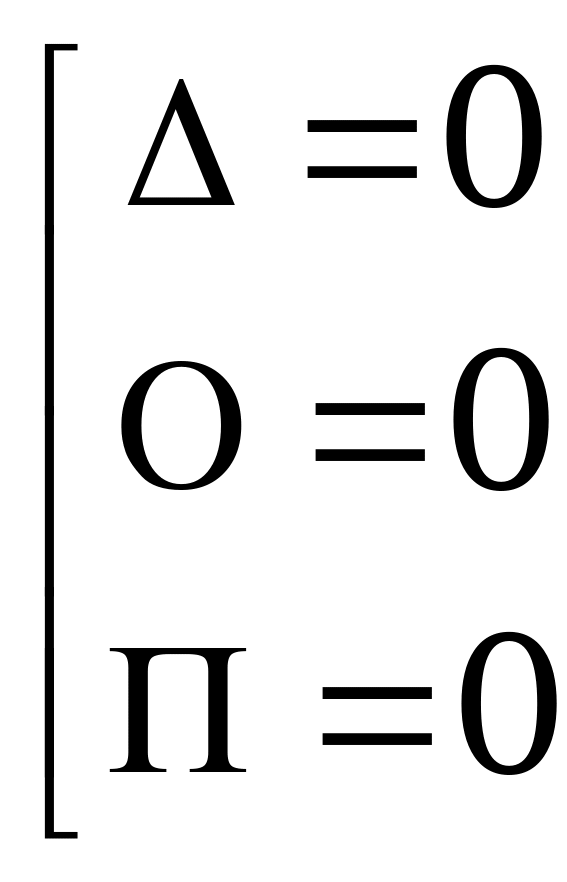
Пример 2. ![]()
Разложим левую часть уравнения на множители. Применим для этого способ группировки. Сгруппируем первое слагаемое со вторым и третье с четвертым.
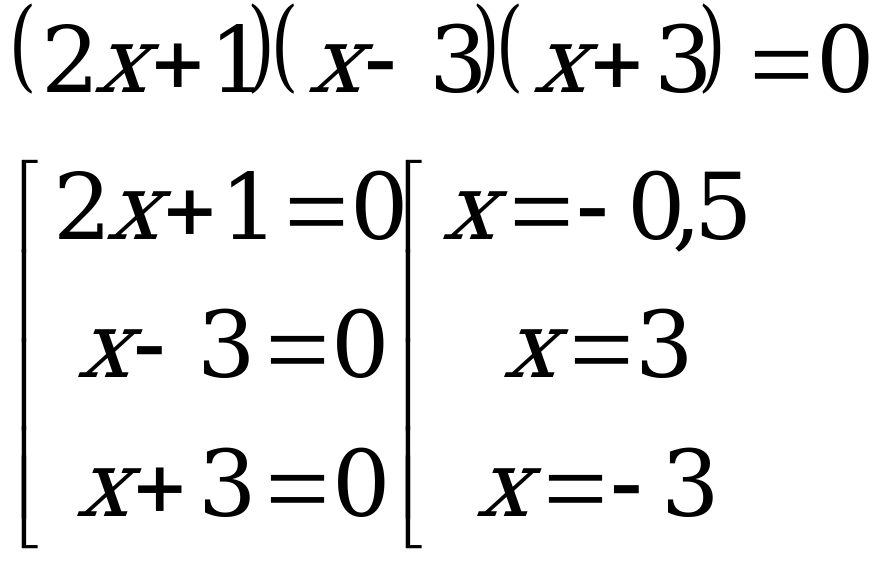
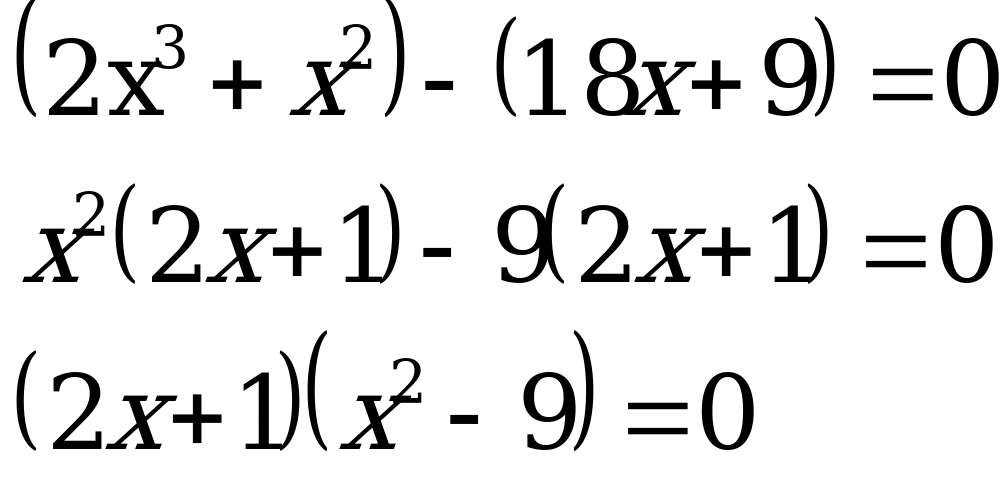
Ответ: ![]()
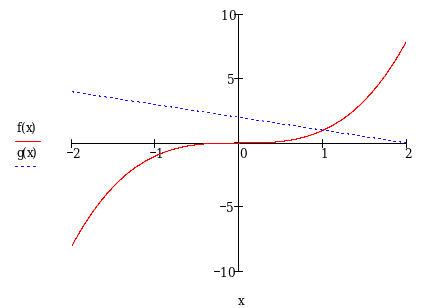
Иногда при решении уравнений ни один из аналитических методов не дает результата. В этом случае можно прибегнуть к графическому решению уравнения. Для этого сначала уравнение следует представить в виде ![]() , где в левой и правой частях находятся известные функции. Затем в одной системе координат строятся графики этих функций. Абсциссы точек их пересечения и есть корни уравнения. Следует отметить, что этот способ не всегда дает точное значение корней – это его недостаток. Но он позволяет определить количество корней, и промежутки в которых они находятся.
, где в левой и правой частях находятся известные функции. Затем в одной системе координат строятся графики этих функций. Абсциссы точек их пересечения и есть корни уравнения. Следует отметить, что этот способ не всегда дает точное значение корней – это его недостаток. Но он позволяет определить количество корней, и промежутки в которых они находятся.
Пример 3. Решить уравнение ![]() .
.
Уравнение является кубическим и для его решения аналитические формулы не известны., поэтому можно прибегнуть к графическому методу.
Представим уравнение в виде ![]() . В одной системе координат строим графики функций
. В одной системе координат строим графики функций ![]() .
.


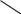

![]()
![]()

Ответ: х =1.
![]()
Задания для самостоятельного решения:
1. (х2 – 3х)2 – 2(х2 – 3х) – 8 =0
2. (х2 – 5х)(х2 – 5х +10) + 24 = 0
3. ![]()
4. ![]()
5. ![]()
6. ![]()
7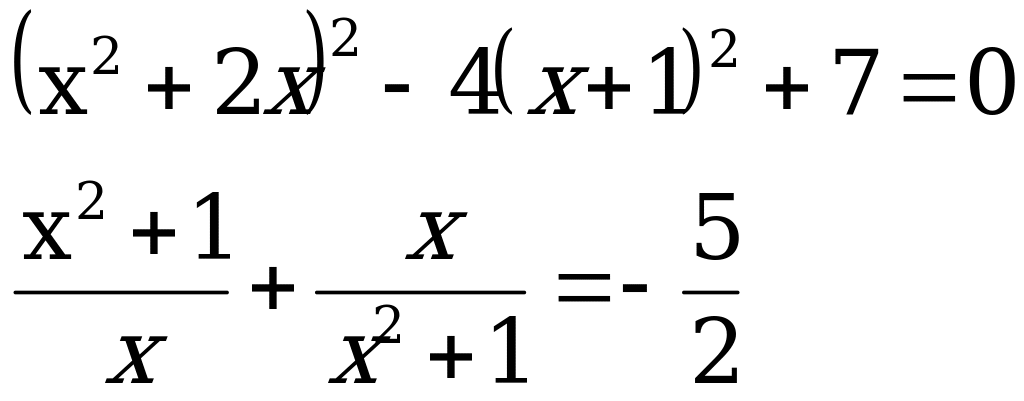 .
.
8.*
9*
10. х3 + х – 10 =0
11. ![]()
Т![]() ема 3. Решение иррациональных уравнений.
ема 3. Решение иррациональных уравнений.
У![]()
![]() равнение с одной переменной называют иррациональным, если хотя бы одна из функций или содержит переменную под знаком радикала.
равнение с одной переменной называют иррациональным, если хотя бы одна из функций или содержит переменную под знаком радикала.
При решении иррациональных уравнений необходимо установить область допустимых значений переменных, исходя из условия, что все радикалы, входящие в уравнение, должны быть арифметическими. Чаще вместо отыскания ОДЗ уравнения проще решить уравнение без учета ОДЗ и сделать в конце решения проверку найденных корней.
Основные методы решения:
Возведение левой и правой части в одну и ту же степень
Поочередное возведение в степень, уединяя радикал
Замена переменной.
Разложение на множители.
Продемонстрируем на следующих примерах:
| П
|
|
| П Пусть тогда Исходное уравнение примет вид: к Решая уравнение , получаем О | Пример 4. Данное уравнение равносильно совокупности следующих условий: Последнее условие необходимо добавить для того, чтобы учесть область допустимых значений уравнения. Вместо этого можно сделать проверку найденных корней уравнения, которая отбросит х=1, так как при этом значении подкоренное выражение становится меньше нуля. Ответ: х1=2, х2=4. |
Задания для самостоятельного решения:
Обязательный уровень
4 + х = ![]()
х + 1 = ![]() :
:
![]()
![]()
1 - х = ![]()
![]()
![]()
![]()
![]()
![]()
Достаточный уровень
11. ![]()
12. ![]()
13. ![]()
14. ![]()
15. ![]()
Тема 4*. Уравнения с модулем.
При решении уравнений, содержащих переменную под знаком модуля, как правило, поступают следующим образом:
Находят ОДЗ уравнения.
Находят такие значения х, которые каждый модуль обращают в нуль.
Найденными в п.2 значениями разбивают ОДЗ на промежутки (на чертеже) и определяют знак подмодульного выражения на каждом промежутке. Это можно сделать методом пробной точки: из рассматриваемого промежутка выбрать пробную точку и подставить это значение под модуль, определить знак полученного выражения.
Рассматривая каждый промежуток в отдельности, раскрыть модуль на каждом из них, с учетом того знака, который принимает модуль на этом промежутке. (Иногда целесообразно объединить несколько промежутков, если модуль на них принимает значения одинаковых знаков).
Р![]() ешить уравнение без модуля и убедиться, что найденный корень принадлежит рассматриваемому промежутку.
ешить уравнение без модуля и убедиться, что найденный корень принадлежит рассматриваемому промежутку.
Пример 1. ![]()
![]() ОДЗ:
ОДЗ: ![]()
![]()

![]() 2
2
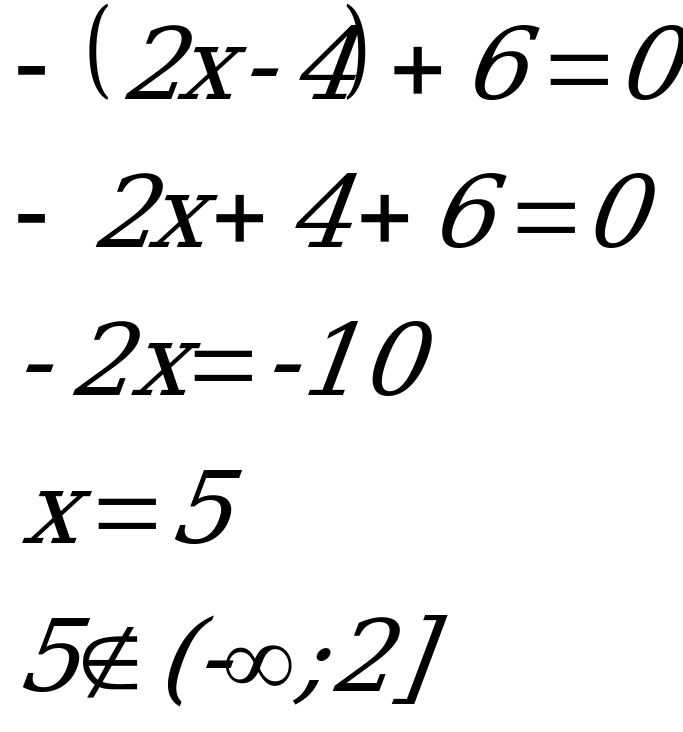
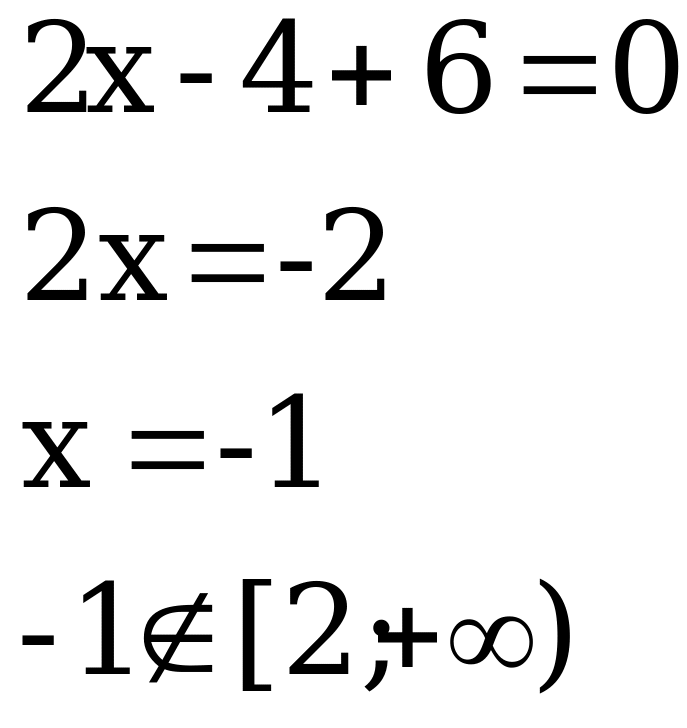
Ответ: решений нет
Пример 2.
ОДЗ: ![]()
![]()
![]()



![]()
![]()
![]()
![]()
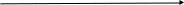
-1 1 2
1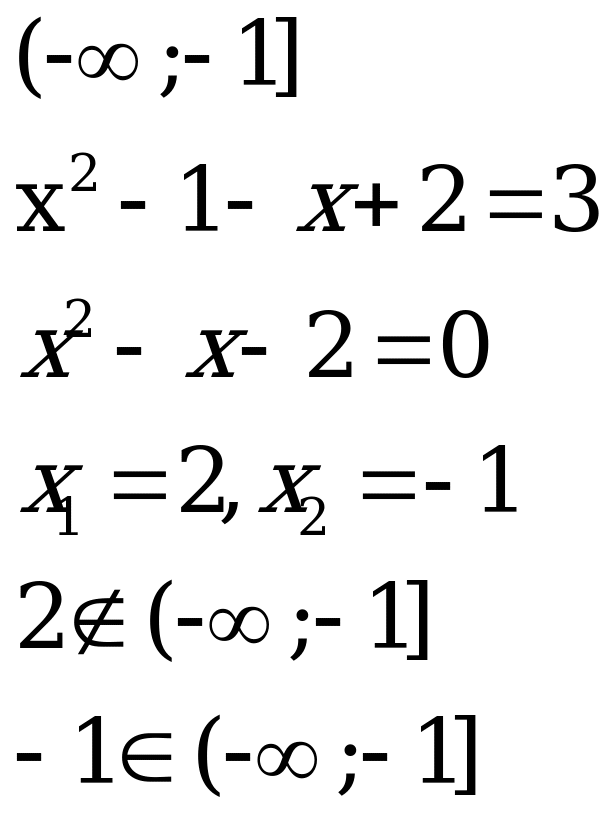 . 2. [-1;1]
. 2. [-1;1]

3. [1;2] 4. [2;+)
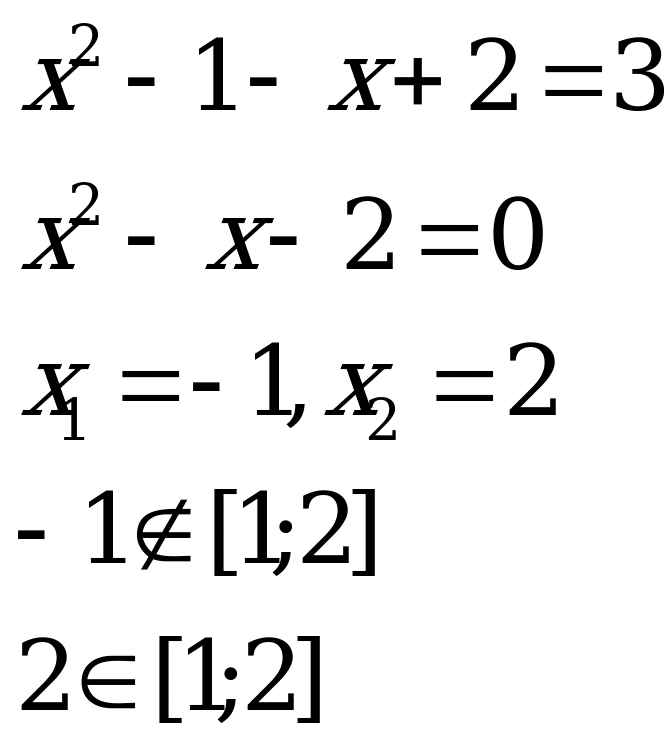
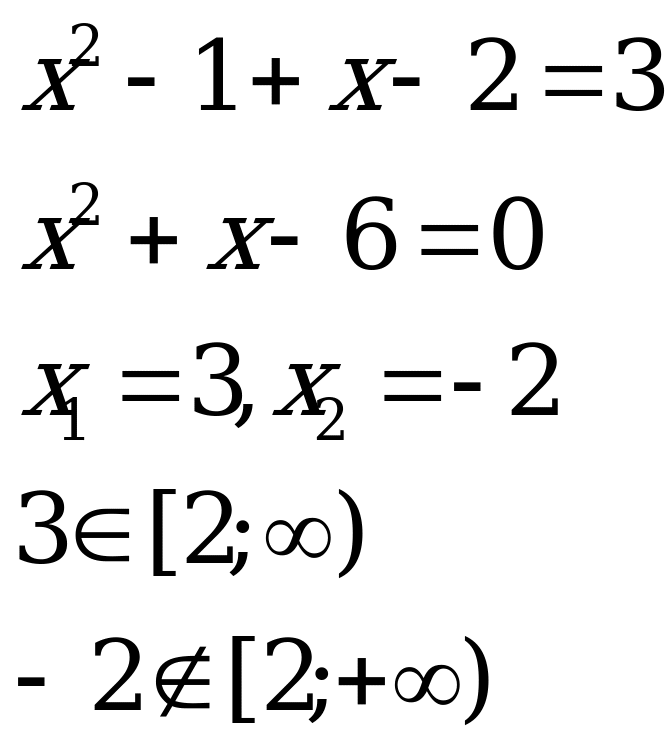
Ответ: {-1; 0; 2; 3}
Задания для самостоятельного решения:
1. ![]()
2. ![]()
3. ![]()
4* ![]()
5* ![]()
Тема 5 Решение неравенств 1-ой и 2-ой степени (повторение).

П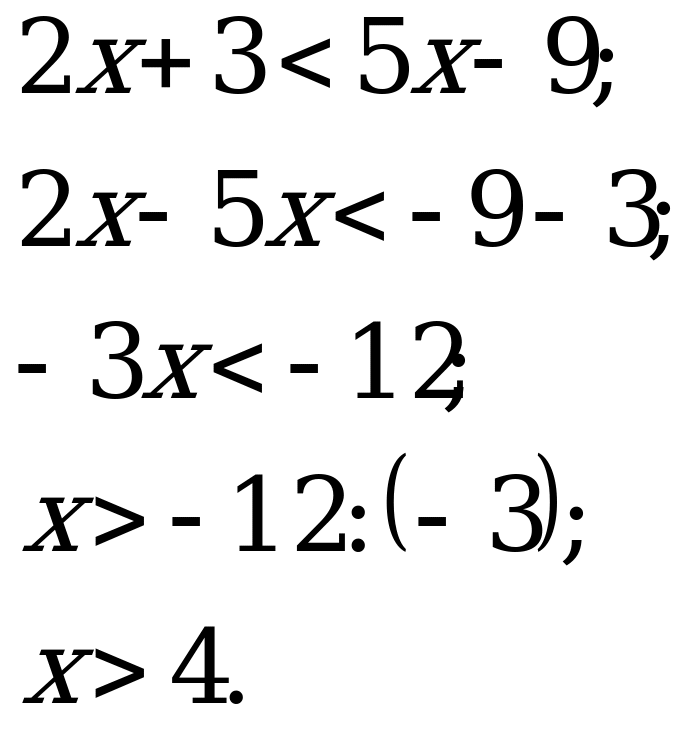 ример 1. Решить неравенство
ример 1. Решить неравенство


 ○ х
○ х
4
Ответ: ![]()
В основе решения квадратного неравенства лежит графический метод. В зависимости от знака коэффициента а и дискриминанта D возможен один из шести случаев расположения графика соответствующей квадратичной функций (табл. 1).
Т а б л и ц а 1
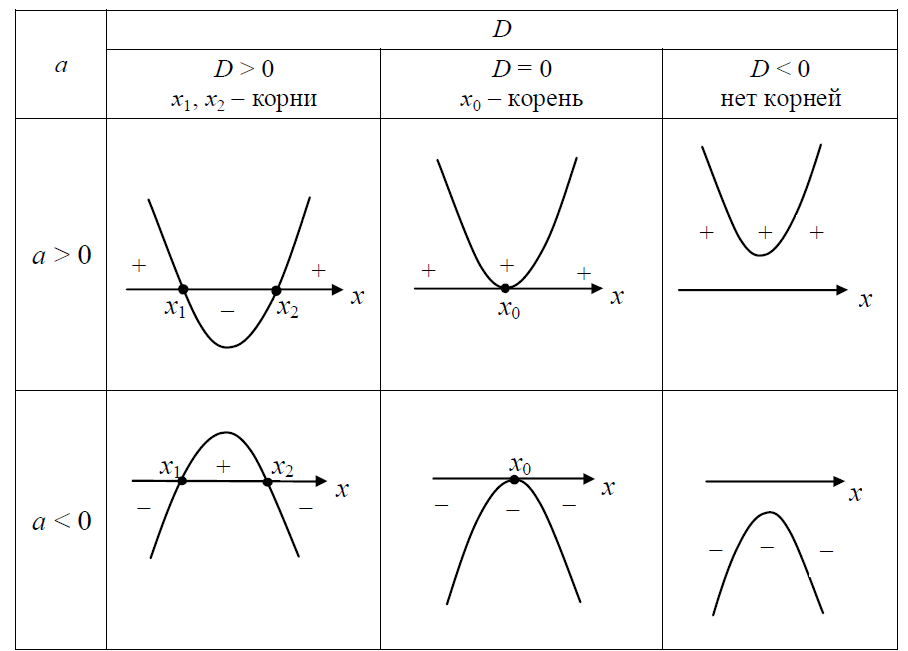
Решение квадратного неравенства находят по расположению соответствующего графика функции относительно оси Ox.
Пример 2. Решить неравенство ![]()
Рассмотрим функцию ![]() Графиком функции является парабола, ветви которой направлены вниз.
Графиком функции является парабола, ветви которой направлены вниз.
Найдем нули функции. Для этого решим уравнение ![]() .
.
Получим ![]() Изобразим схематично график функции и обозначим на графике промежуток, соответствующий неравенству.
Изобразим схематично график функции и обозначим на графике промежуток, соответствующий неравенству.
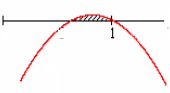

![]() х
х
![]()
![]()
Ответ: ![]() .
.
Задания для самостоятельного решения:
1. ![]()
2. ![]()
3. ![]()
4. ![]()
5. ![]()
6. ![]()
7. х2 – 6х + 8 ≥ 0
8. – х2 + 6х – 5 ≥ 0
9. х2 + 2х +1 0
10. ![]()
11. ![]()
12. ![]()
13. ![]()
14. ![]()
15. ![]()
Тема 6 Метод интервалов.
Методом интервалов, как правило, решается неравенства вида:
1) ![]()
2) ![]()
В общем случае метод интервалов состоит в следующем:
1. Рассмотреть функцию у(х), равную левой части неравенства
2. Найти область определения этой функции
3. Найти нули функции
4. На числовой прямой область определения разбить на промежутки нулями функции.
5. Определить знак функции на каждом из полученных промежутков (используя, например, метод пробной точки или правило чередования знаков)
6. Записать ответ.
Пример 1. Решить неравенство: ![]()
Приведем с помощью разложения на множители методом группировки неравенство к первому виду:
![]()
Рассмотрим функцию у(х) = ![]() .
.
Область определения этой функции – все действительные числа.
Н ули этой функции:
ули этой функции: ![]()
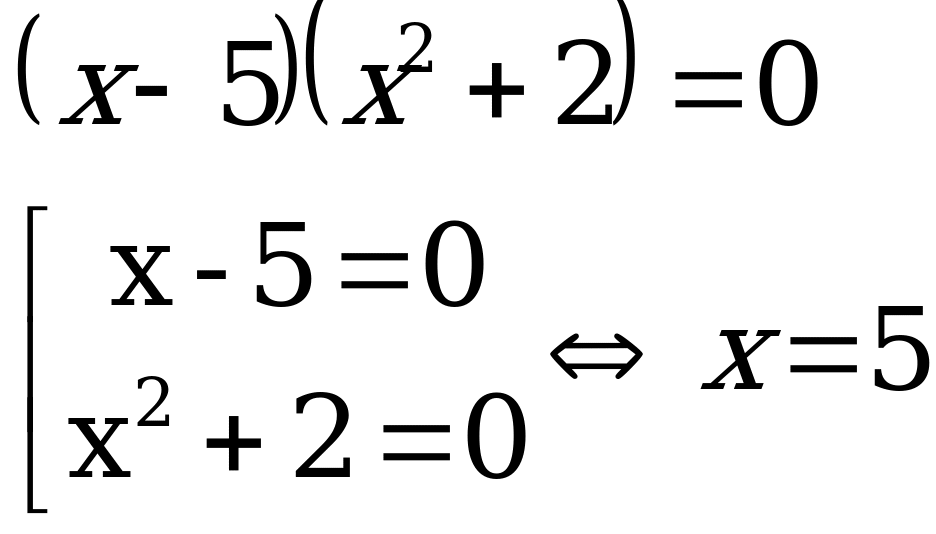
![]()

5
Ответ: ![]()
Пример 2. Решить неравенство: ![]() .
.
Рассмотрим функцию у(х) = ![]() .
.
Область определения этой функции – все числа, кроме тех, которые знаменатель обращают в нуль, т.е. ![]()
Н ули функции:
ули функции: ![]()


 + + +
+ + +

-4 0,5 3 х
Ответ: ![]()
Пример 3. ![]() .
.
Это неравенство первого вида. Рассмотрим функцию у(х) = ![]() .
.
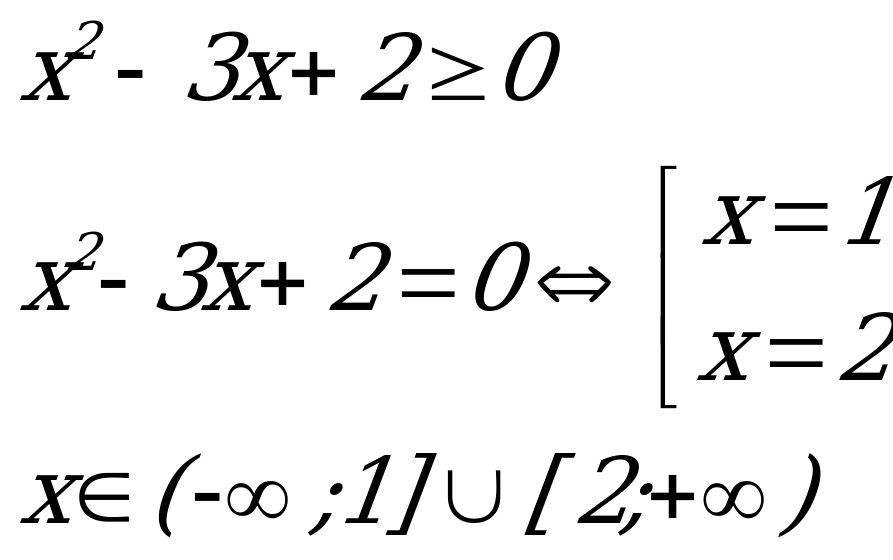
Область определения:
Н ули функции:
ули функции: 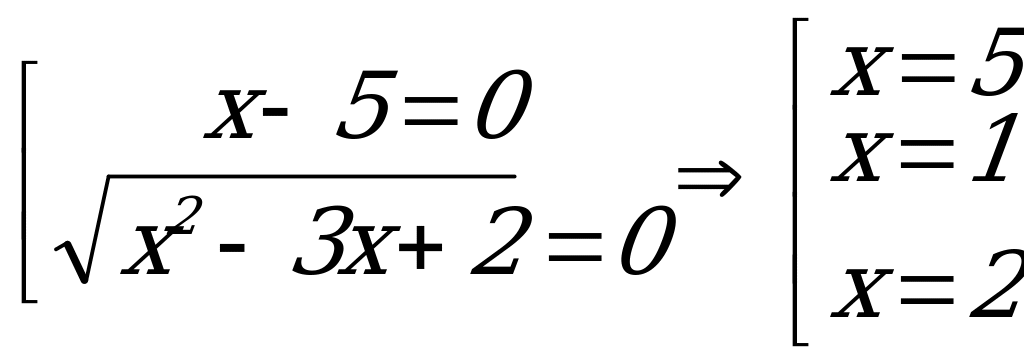
+


 _ _
_ _
1 2 5
Ответ: ![]()
Задания для самостоятельного решения:
( х +2)(х+1)(х-3)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Тема 7*. Решение иррациональных неравенств и неравенств с модулем.
К иррациональным относятся неравенства, в которых неизвестная переменная находится под знаком радикала. Существует несколько методов решения иррациональных неравенств. Первая группа методов является аналитической и зависит от вида неравенства. Общая схема приведена в таблице 2.
Т а б л и ц а 2.
а б л и ц а 2.
Пример 1. Решить неравенство: ![]()
Аналитический метод.
Перейдем к равносильной системе:![]()
-3 -2 -1 1
Ответ: ![]()
Метод интервалов.
Перенесем все слагаемые влево: ![]()
Рассмотрим функцию у(х) = ![]()
Область определения функции: ![]()
Н ули функции:
ули функции: ![]()

 х
х
![]() -3 1
-3 1
Ответ: ![]()
Задания для самостоятельного решения:
1![]() .
.![]()
2.
3.
При решении неравенств с модулем так же существует две группы методов: аналитические и интервалов.
Аналитический метод заключается в следующем:
1) найти значения х, для которых выражения, стоящие под модулями, равны нулю;
2) найденные значения х нанести на числовую ось;
3) определить знак выражения f (x) на всех полученных промежутках;
4) нарисовать кривую знаков;
5) раскрыть модуль, пользуясь рисунком, и получить соответствующее неравенство, которое следует решить вместе с условием принадлежности переменной х определенному промежутку;
6) в ответе неравенства указать совокупность полученных решений.
Метод интервалов применяется в обычном виде.
Пример 2 . Решить неравенство:![]() Аналитический метод:
Аналитический метод:
З нак модуля - +
нак модуля - +
-2
1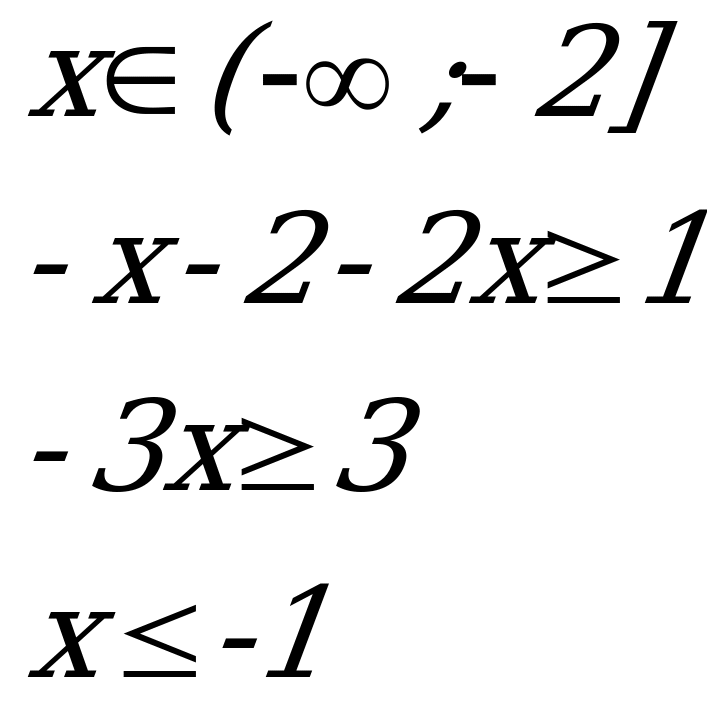
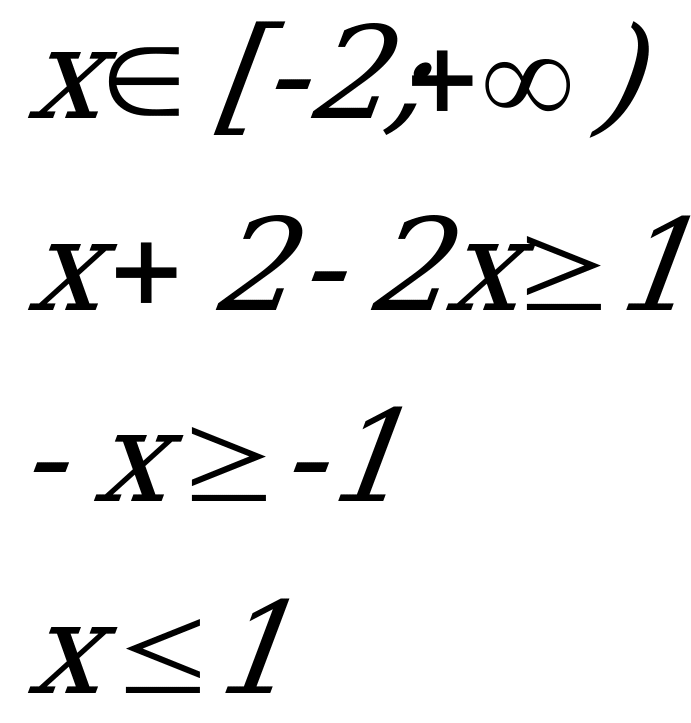 . 2.
. 2.
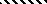
 -2 -1 -2
-2 -1 -2



Ответ: ![]() 1
1
Метод интервалов.
Перенесем слагаемые влево ![]()
Рассмотрим функцию у(х) = ![]()
Область определения функции – все действительные числа.
Нули функции : х = 1


1 -
Ответ: ![]() .
.
Задания для самостоятельного решения:
4. ![]() 8.
8. ![]()
5. ![]() 9.
9. ![]()
6. ![]() 10.
10. ![]()
7. ![]()
Тема 8. Решение систем уравнений с двумя переменными.
При решении систем уравнений применяются следующие методы:
метод сложения
метод подстановки
замена переменной
г рафический метод.
рафический метод.
Пример 1.
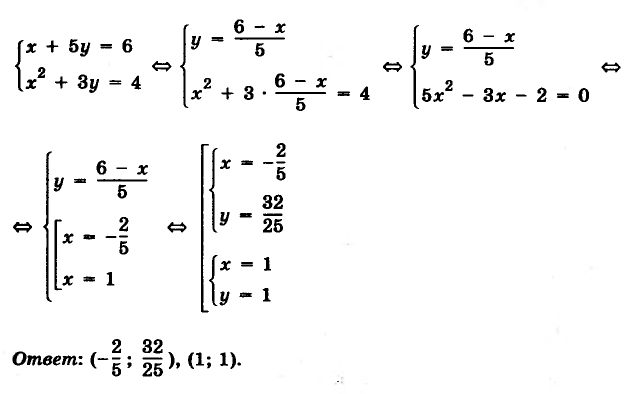
Задания для самостоятельного решения:
1![]()
12
. 2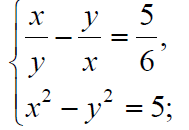 .
. ![]() 4. 6.
4. 6. ![]() 8.
8. ![]()
Разные задачи:
1. От города до поселка автомобиль доехал за 3 ч. Если бы он увеличил скорость на 25 км/ч, то проехал бы это расстояние за 2 ч. С какой скоростью ехал автомобиль и чему равно расстояние от поселка до города?
2. Два велосипедиста отправились одновременно навстречу друг другу из двух пунктов, расстояние между которыми 60 км, и встретились через 2 ч. Определите скорость каждого велосипедиста, если у одного она на 2 км/ч больше, чем у другого.
3. Лодка может проплыть расстояние между двумя селениями, стоящими на берегу реки, за 4 ч по течению реки и за 8 ч против течения. Скорость течения реки 2 км/ч. Найдите собственную скорость лодки и расстояние между селениями.
4. Для распечатки 340 страниц были использованы две копировальные машины. Первая машина работала 10 мин, а вторая — 15 мин. Сколько страниц в минуту печатает каждая машина, если первая печатает в минуту на 4 страницы больше, чем вторая?
5. Двое рабочих изготовили по одинаковому количеству деталей. Первый выполнил эту работу за 5 ч, а второй за 4 ч, так как изготовлял в час на 12 деталей больше первого. По сколько деталей изготовили рабочие?
6. За одно и то же время велосипедист проехал 4 км, а мотоциклист — 10 км. Скорость мотоциклиста на 18 км/ч больше скорости велосипедиста. Найдите скорость велосипедиста.
7. В зале расставили одинаковыми рядами 48 стульев. Рядов оказалось на 8 больше, чем стульев в каждом ряду. Сколько стульев в каждом ряду и сколько рядов в зале?
Ответы к заданиям для самостоятельного решения
| Тема 1. | Тема 2. | Тема 3. | Тема 4. | Тема 5. | Тема 6. | Тема 7. | Тема 8. | Задачи |
| 1. 0; -0,5 | 1. 1; 2;4 | 1. -2 | 1. | 1. (-; -3,5) | 1. (-; -2)[-1; 3) | 1. (-2; 7)(7; ) | 1. (4;3), (3;4) | 1. 75 км/ч, 150 км |
| 2. 0,5 | 2. 1; 2; 3; 4 | 2. 2; 3 | 2. (-; 5] | 2. (1; ) | 2. (-1; 2) | 2. (0;) | 2. (-2; 3), | 2. 14 км/ч, 16 км/ч |
| 3. 3; 6 | 3. 1; 2;4 | 3. -1 | 3. 1; -5 | 3. (-3; -1) | 3. (-; 2)[3,5; ) | | 3. (7;3),(7;-3),(-7;3), (-7;-3) | 3. 6 км/ч, 32 км |
| 4. -2; -6 | 4. 1; 4; 6 | 4. 2 | 4. -1 | 4. (-0.5; 0,5) | 4. (3; 8) (8; ) | 4. (2; 3) | 4. (3;2), (-3;-2) | 4. 12 стр., 16 стр. |
| 5. 0; -1 | 5. 1; 2; | 5. -4 | 5. 1; 3 | 5. (-; -2][3; ) | 5. (-; -8,5)(1; 3) | 5. (- ; +) | 5. (3;2), (3;-2), (4; | 5. 240 дет |
| 6.0 | 6. 2 | 6. 1; 8 |
| 6. [-6; -1] | 6. [-2; 1](2; ) | 6. (- ; +) | 6. (-1; -1) | 6. 12 км/ч |
| 7. 0; -17 | 7. 0; 0,5 | 7. 2 |
| 7. (-; 2] [4; ) | 7. (-; -7)(1; 4) | 7. (- ; +) | 7. (1; 3) | 7. 4 ст. и 12 р. |
| 8. 3; 4 | 8. 1; -3; | 8. |
| 8. [1; 5] | 8. [4; 7)(7; ) | 8. (-; -5][4; ) | 8. (1; 7) | |
| 9.3; | 9. -1 | 9. -2 |
| 9. (-; -1) (-1; ) | 9. (0; 1)(3; ) | 9. (-4; 1) | | |
| 10.1; 5 | 10. 2 | 10. -3 |
| 10. (-; -2] ]2; ) | 10. (0; 6) | 10. [0; 2] | | |
| 11. 3 | 11. 1 | 11. 2; -4,5 |
| 11. (-; -10) (10; ) | 11. (-7; -4] | | | |
| 12. -3 |
| 12. 0; 1 |
| 12. [0; 4] | 12. [-3; -1,5) | | | |
| 13. 0,5;-1 |
| 13. 1 |
| 13. 2 | 13. (3; ) | | | |
| 14.2; -3,5 |
| 14. 6; 9 |
| 14. (-; +) | | | | |
| 15. |
| 15. 4 |
| 15. | | | | |
Домашняя контрольная работа
| № 1. Решить уравнение: | |||
| 1. | 5. | 8. | |
| 2. | 6. | 9. | |
| 3. | 7. | 10. | |
| 4. |
| ||
| №2. Решить уравнение: | |||
| 1. | 5. | 8. | |
| 2. | 6. | 9. | |
| 3. | 7. | 10. | |
| 4. |
| ||
| №3. Решить уравнение: | |||
| 1. | 5. | 8. | |
| 2. | 6. | 9. | |
| 3. | 7. | 10. | |
| 4. |
| ||
| №4. Решить уравнение: | |||
| 1. | 5. | 8. | |
| 2. | 6. | 9. | |
| 3. | 7. | 10. | |
| 4. |
| ||
| №5.Решить уравнение: | |||
| 1. | 5. | 8. | |
| 2. | 6. | 9. | |
| 3. | 7. | 10. | |
| 4. |
| ||
| №6. Решить уравнение: |
| ||
| 1. | 5. | 8. | |
| 2. | 6. | 9. | |
| 3. | 7. | 10. | |
| 4. |
| ||
| №7. Решить уравнение: |
| ||
| 1. | 5. | 8. | |
| 2. | 6. | 9. | |
| 3. | 7. | 10. | |
| 4. |
| ||
| №8. Решить неравенство методом интервалов: | |||
| 1. | 5. | 8. | |
| 2. | 6. | 9. | |
| 3. | 7. | 10. | |
| 4. |
| ||
| №9. Решить неравенство методом интервалов: | |||
| 1. | 5. | 8. | |
| 2. | 6. | 9. | |
| 3. | 7. | 10. | |
| 4. |
| ||
| №10. Решить неравенство: | |||
| 1. | 5. | 8. | |
| 2. | 6. | 9. | |
| 3. | 7. | 10. | |
| 4. |
| ||
| №11. Решить неравенство: | |||
| 1. | 5. | 8. | |
| 2. | 6. | 9. | |
| 3. | 7. | 10. | |
| 4. |
| ||
| №12. Решить неравенство: | |||
| 1. | 5. | 8. | |
| 2. | 6. | 9. | |
| 3. | 7. | 10. | |
| 4. |
| ||
| №13. Решить неравенство: | |||
| 1. | 5. | 8. | |
| 2. | 6. | 9. | |
| 3. | 7. | 10. | |
| 4. |
| ||
| №14. Решить систему уравнений: | |||
| 1. | 5. | 8. | |
| 2. | 6. | 9. | |
| 3. | 7. | 10. | |
| 4. |
| ||
Список рекомендуемой литературы
Алимов Ш.А. и др. Алгебра и начала анализа. 10 (11) кл. – М., 2000.
Башмаков М.И. Алгебра и начала математического анализа (базовый уровень). 10 кл. – М., 2005.
Башмаков М.И. Алгебра и начала математического анализа (базовый уровень). 11 кл. – М., 2005.
Башмаков М.И. Математика (базовый уровень). 10—11 кл. – М., 2005.
Башмаков М.И. Математика: 10 кл. Сборник задач: учеб. пособие. – М., 2004.
Башмаков М.И. Математика: учебник для 10 кл. – М., 2004.
Колмогоров А.Н. и др. Алгебра и начала анализа. 10 (11) кл. – М., 2000.
Колягин Ю.М. и др. Математика (Книга 1). – М., 2003.
Колягин Ю.М. и др. Математика (Книга 2). – М., 2003.
Луканкин Г.Л., Луканкин А.Г. Математика. Ч. 1: учебное пособие для учреждений начального профессионального образования. – М., 2004.
Пехлецкий И.Д. Математика: учебник. – М., 2003.
Заключение.
В результате изучения данной темы студент приобретет знания по основным приемам решения алгебраических и иррациональных уравнений и неравенств. Студент будет уметь:
решать целые, рациональные, иррациональные, сводящиеся к линейным и квадратным уравнения, а также аналогичные неравенства и системы;
использовать графический метод решения уравнений и неравенств;
составлять и решать уравнения и неравенства, связывающие неизвестные величины в текстовых (в том числе прикладных) задачах.
2

 Получите свидетельство
Получите свидетельство Вход
Вход


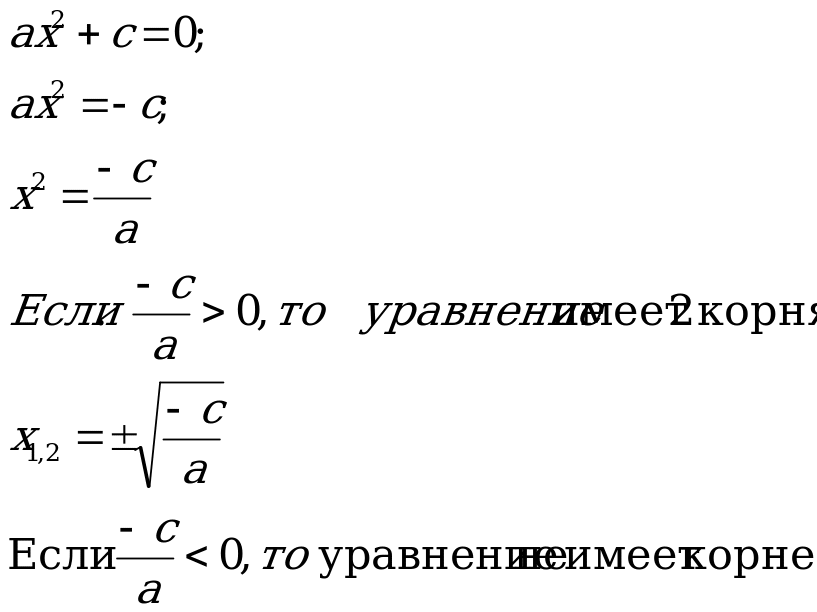
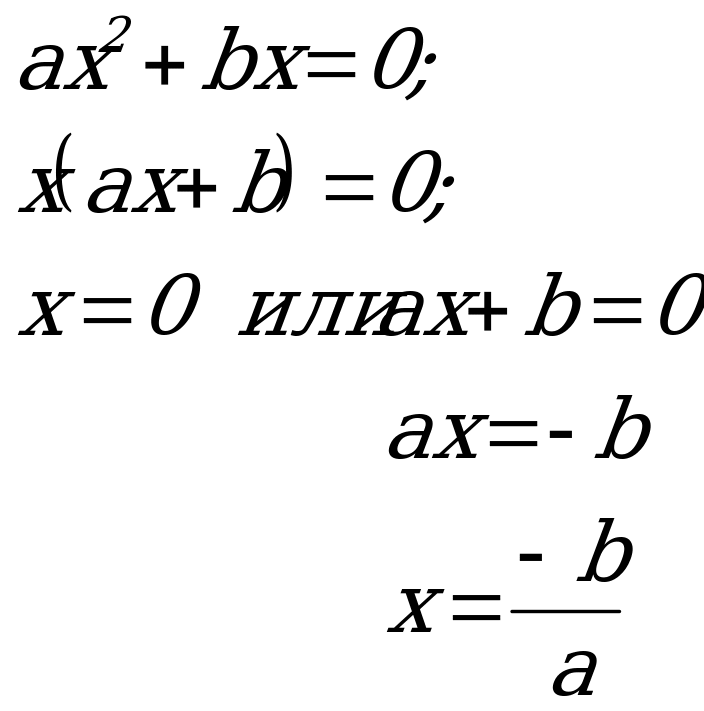
 ример 1.
ример 1.  Пример 2.
Пример 2. 








 Виды уравнений и неравенств (1023.5 KB)
Виды уравнений и неравенств (1023.5 KB)
 0
0 257
257 0
0 Нравится
0
Нравится
0








