Тригонометрические неравенства. Методы их решения

Простейшие тригонометрические неравенства

Алгоритм решения неравенств с помощью единичной окружности

Заменить неравенство уравнением (устно) и отметить на единичной окружности точки, соответствующие уравнению.

Отметить на единичной окружности точки, соответствующие неравенству (выделить соответствующую дугу).

Указать направление отсчёта (на выделенной дуге отмечается положительное направление, т. е. против часовой стрелки).

Найти начало дуги и угол, ему соответствующий (меньший угол).

Найти конец дуги и угол, ему соответствующий (больший угол).

Записать ответ в виде двойного неравенства с учётом периодичности функции (слева – угол, соответствующий началу дуги).

Записать ответ в виде промежутка.

Алгоритм решения тригонометрических неравенств

графическим способом

Заменить неравенство уравнением и построить графики функций y=f(x) , где f(x) – одна из тригонометрических функций, и y=a.

Отметить точки пересечения графиков функций y=f(x) и y=a, найти абсциссы этих точек.

Отметить ту часть графика, которая соответствует данному неравенству.

На главном периоде выделить промежуток оси x, на котором выполняется заданное неравенство.

Записать ответ в виде двойного неравенства (слева-меньший угол) с учётом периодичности функции.

Записать ответ в виде промежутка.

Задания: №№ 22.42, 22.43, 22.46, 22.47, 22.50,  22.51 (А.Г. Мордкович)

№№  11.32-11.42 (С.М. Никольский)

Неравенства, приводимые к простейшим

С помощью введения нового неизвестного t=ax+b

Суть метода: введя новую переменную t=ax+b, привести неравенство к простейшему виду. Решить полученное неравенство для переменной t. Затем вернуться к переменной x и найти её значение. Записать ответ в виде промежутка.

С помощью основных тригонометрических формул.

Суть метода: используя основные тригонометрические формулы, приводим неравенство к простейшему виду. Далее применяем алгоритм решения простейших тригонометрических неравенств.

Неравенства, решаемые заменой переменной

1.Приводимые к квадратным или рациональным заменой

t=f(x), где f(x) - одна из тригонометрических функций.

Неравенства, решаемые методом интервалов

Алгоритм решения тригонометрических неравенств методом интервалов.

С помощью преобразований привести неравенство к виду f(t)>0 (f(t)<0)  (если это необходимо).

Найти основной период Т функции f (Т равен НОК периодов, входящих в неравенство тригонометрических функций).

Найти нули функции f(t) на промежутке , решив уравнение f(t)=0.

Найти точки разрыва функции f(t) на этом промежутке.

Найденными точками разделить отрезок  на части, в каждой из которых функция f(t) имеет постоянный знак.

Определить знак функции в каждой части методом пробных точек (результат удобно оформить в виде таблицы).

Выбрать те части, в которых выполняется исходное неравенство.

Учитывая периодичность функции, записать решение исходного неравенства.

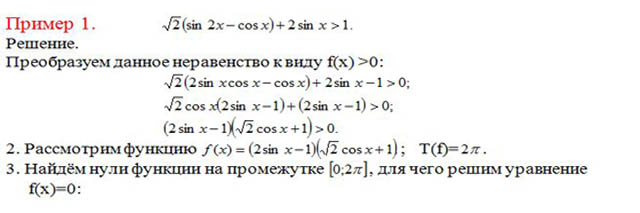
Весь материал  - в документе.