ИДЕИ МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ В РЕШЕНИИ ТЕКСТОВЫХ ЗАДАЧ НА ПРОЦЕНТЫ И СМЕСИ.
| Жанна Робертовна Юрова, МБОУ «СОШ№13»,учитель |
| математики, тел. 89232041902 |
|
«Главная сила математики состоит в том, что вместе с решением одной конкретной задачи она создает общие приемы и способы, применимые во многих ситуациях, которые не всегда можно предвидеть». М. Башмаков |
Проценты - традиционно одна из слабо усваивающихся тем школьного курса. Большинство школьников, включая выпускников, панически боится задач, связанных с понятием «проценты». И этот факт очень прискорбен в наш стремительный век кредитов и ипотек, различного рода распродаж и скидок, а также – всевозможных финансовых операций с банковскими вкладами и т. д. Ведь не зря в 2012 году была пересмотрена структура ГИА, которая теперь совершенно справедливо включает в себя модуль «Реальная математика».
И так, в настоящее время математика, как никогда, все шире проникает в повседневную жизнь, которая требует от нас новых знаний и умений. Сегодня важно, чтобы люди, понимали, как распоряжаться своими деньгами, как оценить свои доходы, как считать свои налоги, т.е. умели применить знания из математики в повседневной жизни. Бытовая математика сегодня нужна практически всем, навыки устного счета необходимы любому человеку.
Поэтому мой выбор изучения темы «Идеи математического моделирования в решении текстовых задач на проценты и смеси» более чем логичен, особенно если учитывать тот факт, что на ЕГЭ и ОГЭ одним из важных проверяемых элементов содержания является умение решать практическую задачу, составляя математическую модель предложенной в ней ситуации.
Статистические данные анализа результатов проведения единых экзаменов по математике говорят о том, что решаемость задания, которое содержит сюжетную задачу, составляет год от года чуть больше или меньше 30%. Такая ситуация позволяет сделать вывод, что большинство учащихся не в полной мере владеет техникой решения текстовых задач и не видит за их часто нетрадиционной формулировкой типовые задания, которые были достаточно хорошо отработаны на уроках в рамках школьной программы. И это также, несомненно, является одной из важнейших причин необходимости более глубокого изучения этого традиционного раздела элементарной математики.
Методике обучения учащихся средней школы решению текстовых задач посвящены работы многих исследователей, данный вопрос неоднократно поднимался в отечественной дидактике обучения математике. Так В.Г. Болтянский, Л.В. Виноградова, В.А. Далингер, К.С. Муравин и Г.К. Муравин, Ф.А. Орехов, Д. Пойа, В.Ф. Чаплыгин, В.Я. Шевцов и др. исследовали потенциал различных методов решения текстовых задач в обучении математике и развития интеллектуальной сферы школьников. Г.В. Дорофеев, И.В. Дробышева, К.К. Ким, И.В. Микляева, Н.К. Рузин и др. изучают влияние текстовых задач на мотивацию учебной деятельности учащихся, а В.П. Радченко, Г.Е. Крейдлин и А.Д. Шмелев исследуют проблему языкового анализа условия текстовой задачи как средства развития продуктивного мышления. Вопросы повышения эффективности обучения решению текстовых задач средствами моделирования рассматриваются в работах А.Г. Грекуловой, К.А. Загородных, М.Т. Кац, И.А. Мешковой, А.Я. Цукаря и др. Анализ указанных работ позволяет сделать вывод, что работа с текстовыми задачами осуществляется при традиционной классно-урочной системе.
В современных условиях актуализировалась проблема обучения решению текстовых задач с использованием информационно-коммуникационных технологий, а именно: среди достижений педагогической науки имеют место отдельные приемы использования интерактивной доски при обучении учащихся девятых классов решению текстовых задач на процессы алгебраическим методом, которые являются частью процессуального компонента методики дифференцированного обучения решению текстовых задач с использованием интерактивных компьютерных средств. Данная методика прошла длительную апробацию в школах Волгограда и Волгоградской области.
В этой методике исходят из того, что текстовая задача представляет собой словесную модель ситуации, в которой описываются лишь количественные и функциональные характеристики процессов или явлений. Поэтому можно для задач на процессы унифицировать систему вопросов, регламентирующую поиск пути решения и составление математической модели задачи в виде уравнения, неравенства или их систем. Конечно, использование этой методики предполагает наличие в кабинете математики интерактивной доски, но, к сожалению, такой «роскошью» обладает не каждый кабинет математики.
Вообще, над проблемой решаемости текстовых задач я начала работать, еще учась в Поволжской государственной социально-гуманитарной академии (годы обучения - с 2004 по 2010) , в институте математики, физики и информатики, где на втором и третьем курсах выполнила и защитила с оценкой «отлично» две курсовые работы по темам «Олимпиадные задачи», «Текстовые задачи как средство обучения учащихся математическому моделированию», а также - дипломную работу на кафедре методики преподавания математики - «Математическое моделирование как средство обучения учащихся основной школы в решении текстовых задач». В своих работах я рассмотрела множество приемов математического моделирования в решении сюжетных задач, которые использовала в своей практике, но все это не позволяло получить ожидаемого результата.
Проблема неумения учащимися решать текстовые задачи, а именно такие, где в условии задействованы проценты, стоит очень остро еще и потому, что в школьных учебниках, к большому сожалению, нет целостной системы в обучении методике решения текстовых задач. В основном, учащиеся знакомятся с алгоритмами решения уравнений, неравенств, а также их систем. Текстовые задачи предлагаются весьма элементарного содержания с одним — двумя условиями. При этом упускается из вида главная задача в обучении математике — развитие логического мышления, которая предполагает умение учащихся оперировать с логическими цепочками умозаключений.
Кроме того, страдает и практическая цель в обучении математике — научить школьников решать задачи из повседневной жизни, что связано с умением составить математическое описание модели.
Я прорешала огромное количество текстовых задач, но с удивлением открыла для себя тот факт, что существуют, казалось бы, простые задачи на проценты, вызывающие порой затруднения в решении даже у меня, учителя, причем, работающего над этой проблемой не один год! Чего же тогда мне ждать от учеников? А ждать некогда, нужно было срочно что-то предпринимать!
Текстовым задачам на проценты и смеси, задачам, в которых речь идет о вкладах в банк под тем или иным процентом, о прибыли, о выполнении плана, об изменении цены на товар; задачам, в которых происходит преобразование исходного вещества (при сушке, при выпаривании) мой сегодняшний доклад посвящается…
Столкнувшись с проблемой, я проштудировала множество трудов своих коллег по названной теме и наконец-то нашла для себя наиболее приемлемый метод, который, естественно, тщательно проанализировала, отбросила что-то, что-то рассмотрела более углубленно и сразу же начала применять на своих уроках. В чем же он заключается?
Русский педагог К.Д. Ушинский указывал, что наглядность отвечает психологическим особенностям детей, мыслящих "формами, звуками, красками, ощущениями".
Баева Л. В., учитель математики из г. Набережные Чалны на своих уроках математики занимается рисованием! Она рисует задачи на проценты, т. е. задачи изображаются в виде отдельных иллюстраций - моделей, и их решение становится почти очевидным!
Ни для кого не секрет, что при первом знакомстве учащихся с обыкновенными дробями наиболее целесообразно, даже необходимо проиллюстрировать проблему. Предположим, нам нужно понять, сколько составит 1/5 от числа. Что будет более наглядным для ученика, чем нарисованный торт, разделенный на 5 частей? А 2/5 от числа? Естественно, мы возьмем 2 куска от разделенного на 5 частей тортика. Торт является математической моделью реальной ситуации и означает наше число. Предположим, оно равно 10. Тогда 1/5 часть от числа 10 будет:
10 : 5= 2, а 2/5 от того же числа – 10 : 5 ∙ 2=4.
А можно ли нарисовать задачи на проценты? Оказывается. Можно!
Вообще, способ решения задач данного типа через определение процента очень громоздок. Как убедительно показать, что 1% – это всего лишь сотая часть числа?
Мой педагогический опыт сложился так, что я как-то пока преподаю только в старших классах. Практика показала, что, к сожалению, ученики, которые приходят ко мне в 9 классе, не обладают обязательным спектром теоретических знаний и практических навыков в решении задач на проценты. Хотя должны обладать... Поэтому я, как говорится, начинаю все сначала… Перед началом изучения в 9-ых классах задач на проценты, я провожу с учениками так называемый мной «теоретический и практический ликбез». Заранее прошу их прийти на урок алгебры с цветными карандашами. И вижу недоумение, написанное на лицах моих учеников! Это очень хорошо! Удивление, а значит заинтересованность – тоже неплохая мотивация!
Затем на уроке предлагаю выполнить ряд заданий, постепенно усложняющихся.
Задание 1.
Заштрихуйте на рисунке указную часть прямоугольника:
20%
50%
30%
70%
Задание 2.(чуть посложнее)
Закрасьте на рисунке 20% прямоугольника, затем другим цветом 25% оставшейся части, а третьим цветом 50% нового остатка. Сколько процентов от прямоугольника составляет незакрашенная часть?
В этих заданиях вопрос и ответ заложены в модель-рисунок, остается только посчитать квадратики и дать ответ на поставленный вопрос задачи.
Ответ: останется 6 клеток(30%)
Это только - подготовительные задания, необходимые для того, чтобы ученики сами могли составлять такие модели по условию задачи, а затем элементарно считывать с них ответ.
Задание 3.
Какую часть первой полоски составляют основные полоски?
(2/5, 4/5,3/5,6/5)
Сколько процентов от первой полоски составляют остальные полоски? (2- 40%, 3 - 80%,4 - 60%,5 - 120%)
Сколько процентов от третьей полоски составляют остальные полоски?(1 - 125%, 2 – 50%, 4 – 75%, 5 – 150%)
Почему ответы различны при одном и том же рисунке? Запомним это: важно с чем сравниваем, иными словами – что принимаем за целое или 100%.
Задача 1. Двое работников получали одинаковую зарплату. С нового года первому работнику увеличили зарплату на 25%, второму – на 50%. На сколько процентов зарплата второго работника больше зарплаты первого?
Пусть зарплата каждого была 4 части (в условии упоминается повышение на 25%, то есть на четверть).
Тогда после повышения у первого она стала составлять 5 частей.
А у второго – 6 частей.
Видим, что зарплата второго работника больше зарплаты первого (ведь теперь эту величину принимаем за 100%) на 20%.
Важный факт, о котором не нужно забывать: за 100% принимают ту величину, с которой сравнивают. В данном случае это – 5 клеток, «зарплата» первого рабочего после повышения. Т. е. уже 100:5=20 Если же сравнить зарплату первого рабочего с зарплатой до повышения, то это будет 25% . Теперь посчитаем, насколько клеток зарплата второго рабочего стала больше первого. На одну, т.е. 1 ∙ 20 = 20%. Никаких громоздких вычислений! Ученики приходят в восторг от увиденного.
Особенно убедительно применение такого изображения при решении задач следующего типа.
Задача 2. Книга дороже альбома на 25%. На сколько процентов альбом дешевле книги?
Большинство не сомневается, что на 25%. Многолетний опыт решения задач подтверждает, что если одна величина больше другой на 25 единиц, то вторая меньше первой тоже на 25 единиц. Предлагаю ученикам поспорить. Изобразим цену альбома отрезком из 4-х частей, тогда цена книги – 5 частей.
Альбом
Книга
Если же принять цену книги за 100%, то видим, что цена альбома составляет 80% цены книги. И альбом дешевле книги на 20%.
Следует заметить, что если сравнивать цену книги по сравнению с альбомом, получается совсем другой ответ. Поэтому своим ученикам еще раз указываю на вопрос задачи. Ключевое слово здесь «книги».
Альбом
Книга
Если же принять цену альбома за 100%, то цена книги будет 100:4=25, т.е. 100+25=125. И ответ будет 25%. Так разрушаются сформированные годами стереотипы. Так значит, правильный ответ на вопрос задачи будет все-таки 20%!
Ответ: альбом дешевле книги на 20% её стоимости
Сделаем ещё один практичный вывод с помощью рисунка. Для начала заметим, что заштрихованная часть составляет 25% процентов площади прямоугольника.
Как изменилась площадь прямоугольника, если та же часть составляет теперь 50% всей площади?
Итак, фиксированная часть в процентном отношении увеличилась в два раза, площадь прямоугольника при этом уменьшилась в два раза.
Есть множество «коварных» текстовых задач на проценты, в которых какая-то величина остаётся неизменной: количество сухого вещества, соли и т.д. Причем, они все встречаются на ЕГЭ и ГИА. Ученики, как правило, заходят в тупик при решении подобного рода задач. В таких задачах что-то испаряется, разбавляется, высушивается. Тогда, во сколько раз в процентном соотношении увеличилась (или уменьшилась) неизменяемая величина, во столько раз уменьшилось (увеличилось) целое. Иными словами: процентное содержание неизменяемой по массе величины и масса данного вещества обратно пропорциональны.
Задача 4. Влажность купленного арбуза составила 99%. В результате длительного хранения влажность снизилась до 98%. Как изменилась масса арбуза?
Решение. Свежий арбуз на 99% состоит из жидкости и на 1% – из сухой массы. Нарисуем графическую модель условия задачи.
|
Вода-99% массы арбуза |
| Сухая масса – 1% массы арбуза |
В результате усушки количество жидкости уменьшилось и составило 98% от новой, также уменьшившейся массы арбуза. Количество же сухого вещества, оставаясь неизменным, составило 2% от новой массы арбуза. Процентное содержание в арбузе сухого вещества (при неизменной его массе) увеличилось вдвое. Следовательно, масса арбуза в результате усушки уменьшилась вдвое.
|
Вода-98% массы арбуза |
| Сухая масса – 2% массы арбуза
|
Это и есть-ответ.
Следует отметить, что прежде, чем решить эту задачу с помощью графической модели, предлагаю решить ее традиционным способом. Какие только ответы не получаю! Причем, при громоздких вычислениях!
Задача 5. Исследования показали, что цветочный нектар содержит 80% воды, а полученный из него мед содержит 20% воды. Сколько кг нектара надо переработать пчелам, чтобы получить 1 кг меда?
Решение. Нарисуем графическую модель условия задачи.
Нектар
|
80% воды |
| 20%сухого вещества |
Поскольку мед содержит 20% воды, количество же сухого вещества осталось неизменным, поэтому оно составит 80%. Количество же сухого вещества, оставаясь неизменным, составило 20% от массы меда.
Мед
|
20% воды |
| 80% сухого вещества |
Мы видим, что масса сухого вещества меда относится к массе сухого вещества нектара как 4:1. Следовательно, чтобы получить 1 кг меда нужно взять нектара в 4 раза больше, т.е. 1 ∙ 4 = 4кг
Ответ: 4 кг.
Задача 6. Виноград содержит 90% влаги, а изюм — 5%. Сколько килограммов винограда требуется для получения 20 килограммов изюма?
Решение: Нарисуем условие задачи.
Виноград
|
90% воды |
| 10%сухого вещества |
Изюм
|
5% воды |
| 95% сухого вещества |
Видим, что сухое вещество в новой массе составило 100% - 5%=95%. Процентное содержание в винограде сухого вещества (при неизменной его массе) увеличилось в 95%:10%=9,5раз , следовательно, масса винограда в результате усушки уменьшилась в 9,5 раз. И если нам нужно получить 20 кг изюма, то искомая масса винограда будет равна 20∙9,5=190 кг.
Ответ: 190
Задача 7. Цена товара увеличилась на 25%. На сколько процентов ее необходимо уменьшить, чтобы получить первоначальную цену товара?
Решение: Казалось бы, ответ очевиден… Но, как мы уже знаем, все не так-то просто! Нарисуем графическую модель условия задачи. Поскольку 100:25=4, рисуем первую модель из четырех клеток.
Каждая клетка сейчас составляет 25%. Прибавляем к нашему рисунку такую же клетку. Это отображает увеличение зарплаты на 25%.
Теперь, анализируя условие задачи, приходим к выводу, что в полученной модели одна клетка будет составит 100%:5=20%. Сравним еще раз количество клеток в полученных моделях. Одна клетка, равна теперь уже 20%. И опять заметим, что собственно, никаких вычислений, только логические рассуждения!
Ответ: 20%
Задача 8. Цену товара сначала повысили на 50%, затем понизили на 20%. На сколько процентов изменилась первоначальная цена?
Решение: Изобразим первоначальную цену товара в виде полоски из 10 клеток.
Очевидно, этой модели одна клетка будет соответствовать 10%.Увеличим длину полоски на 10:2=5 клеток, т. е. ровно на половину.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
Теперь полученная полоса будет составлять 100%. Читаем вторую часть условия задачи. «Затем понизили на 20 %. Замечаем, что 20% составляет 1/5 часть. Разделим число клеток, равное 15 на 5, получаем 3 клетки. Проиллюстрируем полученный результат.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
Теперь осталось выполнить простейшее арифметическое действие:
12-10=2.А одна клетка изначально у нас равнялась 10%. Следовательно, 2∙10=20.
Ответ: На 20%
Следует заметить, прежде чем проиллюстрировать наши задачи, каждую из них мы сначала вместе прорешиваем алгебраическим методом, чтобы всякий раз проследить разницу в трудоемкости этих двух методов.
К примеру, рассмотрим последнюю задачу.
Алгебраический метод решения.
Пусть х – первоначальная цена товара, тогда 50% от х составит 0,5 х. И цена товара после повышения на 50% составит: х+0,5х=1,5х.
Теперь найдем, сколько составит понижение товара на 20%.
Y=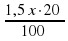 =0,2∙1,5х=0,3х
=0,2∙1,5х=0,3х
А цена товара после понижения на 20% составит: 1,5х-0,3х=1,2х
Поскольку в условии указано, что полученную стоимость нужно сравнить с первоначальной ценой, примем начальную цену за 100%. Опять получаем пропорцию:
Y=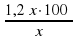 =120%
=120%
Итак, получили, что разница между начальной и конечной ценой составит:120% - 100%=20%.
Ответ: 20%.
А теперь сравним 2 решения. Результат налицо. Первый метод содержит 2 простейшие алгебраические операции, которые выполняются устно, а второй – аж 2 пропорции! Замечаем, что если бы цена товара первоначально увеличивалась не на 50%, а скажем, на 30%, то при не рациональном решении задачи мы бы получили еще и третью пропорцию, и далеко не факт, что все они были бы составлены верно. Да и решение такого количества пропорций могло бы привести к ошибкам в промежуточных вычислениях.
И так, подведем итоги. Несомненно, что этот метод математического моделирования имеет ряд преимуществ:
Мотивация. Детям гораздо интереснее рисовать, нежели выполнять порой изнурительные алгебраические выкладки, требующие к тому же прочных знаний и навыков работы с десятичными и обыкновенными дробями.
Простота умозаключений, которые ничуть не отвергают важнейшей роли текстовых задач - формирование логического мышления у учащихся, так необходимого для усваивания разнообразных тем алгебры и начала анализа. Напротив, решение задач на проценты путем построения графических математических моделей развивают логическое мышление.
Не требует запоминания каких-либо формул.
При участии во всевозможных контрольных испытаниях, а особенно если это касается тестирования, большое значение имеет умение испытуемого экономить время, что позволяет ему отвести больший резерв времени для решения более сложных задач, что в полной мере позволяет этот метод.
Метод графического моделирования наглядно позволяет разрушить сложившиеся неправильные стереотипы, которые бесспорно ведут к неверному решению определенного вида «коварных» задач на проценты.
Из недостатков графического моделирования – очевидно то, что не всякую задачу можно «нарисовать». Порой для того, чтобы правильно проиллюстрировать математическую модель, необходимо посчитать НОД сравниваемых чисел, что может изначально вызвать затруднения у школьников.
Этот метод я считаю определенно перспективным и интересным, а также многогранным в будущем своем развитии. И, безусловно, собираюсь продолжать применять его в своей педагогической практике. Необходимо только соблюсти принцип «от простого - к сложному», и обучать этому методу учеников плавно, тщательно рефлектируя промежуточные результаты.
В начале марта я провела сравнительный мониторинг успеваемости в 9-ых классах и увидела, что метод «работает», и качество знаний заметно улучшилось. Результаты мониторинга представлены мной в Приложении1.
В нынешних 9-ых классах я преподаю второй год и с гордостью хочу отметить, что действительно смотивировала определенное количество своих учеников на изучение проблемы решения текстовых задач. Во время весенних каникул двум моим школьницам было предложено посещение занятий весенней школы «Матрешка» (6 часов) в Гимназии №5, посвященных методике решения текстовых задач, на что они с радостью согласились. И просто в неописуемом восторге пришли после пройденного курса и рассказали мне о своих впечатлениях после посещенных занятий.
В настоящее время с ученицей 9 «а» класса я готовлю к защите научную работу по проблеме решения текстовых олимпиадных задач.
Кроме того, как известно, текстовые задачи включаются и в различные математические испытания – олимпиады, где четверо моих девятиклассников принимают активное участие. Это такие олимпиады, как «Олимпус», «Авангард», «Школьные дни», «Кенгуру». Вместе мы радостью констатируем, что они уже без особого труда выполняют задания, где встречаются сюжетные задачи на вычисление процентов.
В настоящее время я уже работаю над программой элективного курса на 2015-2016 год «Текстовые задачи», рассчитанный, в первую очередь, на учащихся, желающих расширить и углубить свои знания по математике и качественно подготовиться к ЕГЭ и ОГЭ, а также - другим конкурсным экзаменам по математике. В элективную программу я в обязательном порядке включаю изучение метода графического моделирования при решении задач на проценты и смеси.
Главная задача курса: помочь школьникам систематизировать полученные на уроках знания по решению текстовых задач и открыть для себя новые методы их решения, которые не рассматриваются в рамках школьной программы.
Свой доклад хочется закончить словами:
“Предмет математики настолько серьезен, что полезно не упускать случая делать его немного занимательным”.
Паскаль
Приложение 1
![]() Мониторинг уровня знаний по математике в 9 «А» классе
Мониторинг уровня знаний по математике в 9 «А» классе
![]() Мониторинг уровня знаний по математике в 9 «б» классе
Мониторинг уровня знаний по математике в 9 «б» классе
ЛИТЕРАТУРА
1. Фридман Л.М. Логико-психологический анализ учебных задач. – М. : Просвещение, 1977.
2. Максимов Л.К. Учебное моделирование и формирование математического мышления младших школьников // Новые исследования в психологии. - 1987. – № 1.
3. Смыковская Т.К. Формы взаимодействия пользователя с интерактивной доской / Т.К. Смыковская, О.Н. Инева // Вестник Волгоградской академии МВД России. – 2010. – № 1. – С. 121-124.
4. Ляпин С. Е., Методика преподавания математики. М.; 1952.
5. Далингер В. А. Все для обеспечения успеха на выпускных и вступительных экзаменах по математике. Вып. 2. Текстовые задачи, решаемые методом составления уравнений: Учеб. Пособие. Омск: ОмГПУ, 1996.
6.Далингер В. А. Задачи в обучении математике: Методические рекомендации для студентов физ.-мат.фак. педагогических институтов и учителей математике средних школ. Омск: ОГПИ, 1990.
7.Дорофеев Г. В., Седова Е. А. Процентные вычисления: Пособие по математике для общеобразовательных классов и классов экономического профиля. СПб: Специальная литература, 1997.
8.Кац М. Проценты. Математика. Приложение к газете «Первое сентября». М.: Издательский дом «Первое сентября», 2004.
9.Малахова Н. А., Орлов В. В., Методика работы с сюжетными задачами: Учебно-методическое пособие. СПб: РГПУ, 1992.
10.Шевкин А. В. Обучение решению текстовых задач: Книга для учителя. М.: ГАЛС ПЛЮС, 1995.
11.Фридман Л. М., Изучаем математику – М.: Просвещение, 1995.
12.Математика в школе, Научно – методический журнал, 4, 1987.
13.Куканов М. А.,Математика 9-11 классы Моделирование в решении задач – Волгоград, Учитель, 2009
14.Веременюк В. В. КожушкоВ. В,Тесты Практикум по математике, Минск, ТетраСистемс, 2012


 Получите свидетельство
Получите свидетельство Вход
Вход



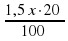 =0,2∙1,5х=0,3х
=0,2∙1,5х=0,3х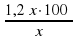 =120%
=120%








 Материал по математике на тему "Идеи математического моделирования в решении текстовых задач на проценты и смеси" (77.83 КB)
Материал по математике на тему "Идеи математического моделирования в решении текстовых задач на проценты и смеси" (77.83 КB)
 0
0 791
791 66
66 Нравится
0
Нравится
0


