Урок "Решение логических задач."

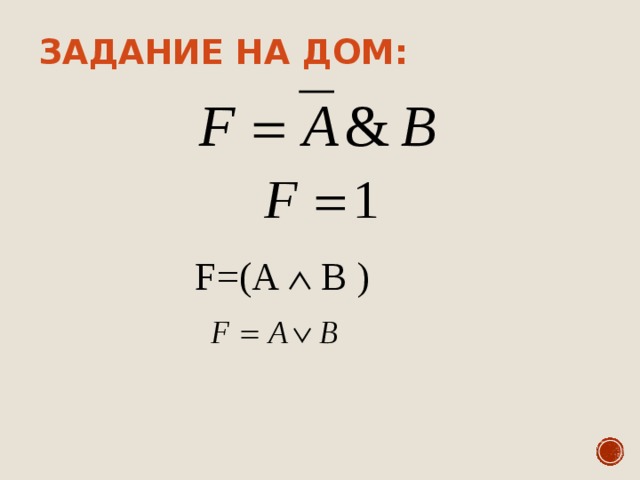
Задание на дом:

F= (A  B )

Задание на дом:

Доказать, двумя способами, что выражения:

равносильны.

Какое логическое выражение равносильно выражению

¬(А & В) & ¬ С

• ¬А v В v ¬ С
• (¬А v ¬ В) & ¬ С
• (¬А v ¬ В) & С
• ¬А & ¬ В & ¬ С

Символом F обозначено одно из указанных ниже логических выражений от трёх аргументов: X,Y,Z. Дан фрагмент таблицы истинности выражения F:

Какое выражение соответствует F?

• ¬ X v Y v ¬ Z
• X & Y & ¬ Z
• ¬ X & ¬ Y & Z
• X v ¬ Y v Z

X

0

Y

1

Z

1

F

0

1

1

0

0

0

1

1

0

X

Y

Z

F

0

1

0

0

1

1

0

1

1

0

1

0

12/6/17

РЕШЕНИЕ ЛОГИЧЕСКИХ ЗАДАЧ

Логические задачи - текстовые задачи, в которых требуется

распознать объекты или расположить их в определенном

порядке по имеющимся свойствам.

При этом часть утверждений условия задачи может быть

истинной или ложной.

Способы решения логических задач:

• Метод рассуждений; Метод таблиц; Использование средств алгебры логики.
• Метод рассуждений; Метод таблиц; Использование средств алгебры логики.
• Метод рассуждений;
• Метод таблиц;
• Использование средств алгебры логики.

Метод рассуждений используется для решения самых

простых логических задач и состоит в том, что мы

проводим рассуждения, используя последовательно все

условия задачи, и приходим к выводу, который и будет

являться ответом задачи.

Задача . Вадим, Сергей и Михаил изучают различные

иностранные языки: китайский, японский и арабский.

На вопрос, какой язык изучает каждый из них, один

ответил: "Вадим изучает китайский, Сергей не изучает

китайский, а Михаил не изучает арабский". Впоследствии

выяснилось, что в этом ответе только одно утверждение

верно, а два других ложны. Какой язык изучает каждый из

молодых людей?

Ответ: Сергей изучает китайский язык, Михаил — японский,

Вадим — арабский.

Задача Классный руководитель пожаловался директору, что у него в классе появилась компания из 3-х учеников, один из которых всегда говорит правду, другой всегда лжет, а третий говорит через раз то ложь, то правду. Директор знает, что их зовут Коля, Саша и Миша, но не знает, кто из них прав, а кто – нет. Однажды все трое прогуляли урок астрономии. Директор знает, что никогда раньше никто из них не прогуливал астрономию. Он вызвал всех троих в кабинет и поговорил с мальчиками. Коля сказал: «Я всегда прогуливаю астрономию. Не верьте тому, что скажет Саша». Саша сказал: «Это был мой первый прогул этого предмета». Миша сказал: «Все, что говорит Коля, - правда».

Саша

Коля

И

Утверждение ИСТИННО , т.к. астрономию никто не прогуливал

Л Л

Миша

Первое утверждение ЛОЖЬ , т.к. астрономию никто не прогуливал, второе утверждение тоже ЛОЖЬ , т.к. Саша говорил правду

Л

Утверждение, что Коля говорил правду ЛОЖЬ

Ответ: Коля лжет всегда, Саша говорит правду , а Миша может сказать правду а может и солгать .

Мама, прибежавшая на звон разбившейся вазы, застала всех трех своих сыновей в совершенно невинных позах: Саша, Ваня и Коля делали вид, что происшедшее к ним не относится. Однако футбольный мяч среди осколков явно говорил об обратном.

- Кто это сделал? - спросила мама.

- Коля не бил по мячу, - сказал Саша.- Это сделал Ваня.

Ваня ответил: - Разбил Коля, Саша не играл в футбол дома.

- Так я и знала, что вы друг на дружку сваливать будете, - рассердилась мама.

- Ну, а ты что скажешь? - спросила она Колю.

- Не сердись, мамочка! Я знаю, что Ваня не мог этого сделать. А я сегодня еще не сделал уроки, - сказал Коля.

Оказалось, что один из мальчиков оба раза солгал, а двое в каждом из своих

заявлений говорили правду.

Кто разбил вазу?

Обозначим утверждения: А - разбил Саша; Б - разбил Ваня; В - разбил Коля.

  Решим методом рассуждения .

По условию двое из мальчиков в каждом заявлении говорят правду, т . е . правы одновременно.

Саша сказал: ¬В & Б

Ваня: В & ¬А

Коля: ¬Б

Саша и Ваня не могут быть одновременно правы, т.к. содержат противоречивые утверждения ¬В и В.

То же самое с Сашей и Колей.

Значит, одновременно правы Ваня и Коля. Т.е. утверждение В истинно.

Разбил Коля. А Саша сказал двойную ложь.

Язык алгебры логики позволяет решать логические

задачи путем построения таблиц истинности или путем

составления и упрощения логического выражения.

Схема решения задачи средствами алгебры логики:

1.  изучается условие задачи;

2.  вводится система обозначений для логических

высказываний;

3.  конструируется логическая формула, описывающая

логические связи между всеми высказываниями условия

задачи;

4.  определяются значения истинности этой логической

формулы;

5.  из полученных значений истинности формулы опред-ся

значения истинности введённых логических высказываний,

на основании которых делается заключение о решении.

Три школьника – Миша(М), Коля(К) и Серёжа(С)- оставшиеся в классе на перемене, были вызваны к директору по поводу разбитого в это время окна в кабинете. На вопрос директора о том, кто это сделал, мальчики ответил следующее:

Миша: «Я не бил окно, и Коля тоже».

Коля: «Миша не разбивал окно, это Сергей разбил его футбольным мячом!»

Сергей: «Я не делал этого, стекло разбил Миша».

Стало известно, что один из ребят сказал чистую правду, второй в одной части заявления согласился, а другое его высказывание истинно, а третий оба факта исказил. Зная это, директор смог докопаться до истины.

Кто разбил стекло в классе?

Решение с помощью таблиц истинности :

Обозначим буквами простые высказывания: М= «Окно разбил Миша, К= «Окно разбил Коля», С= «Окно разбил Сергей». Тогда высказывания мальчиков можно записать с помощью сложных логических выражений:

- высказывание Миши,

- высказывание Коли,

,

- высказывание Миши,

,

- высказывание Коли,

должна иметь значение «истина». Только

-высказывание Сергея.

, или

, или только

По условию задачи только один из мальчиков сказал чистую правду, т. е. только одна из конъюнкций истина.

. При этом: (

)&(

)&(

)=1/

Составим таблицу истинности:

М

К

0

0

С

0

1

1

1

0

0

1

0

1

0

0

0

0

0

0

1

РТ: №89

Три друга играли во дворе в футбол и разбили мячом окно. Ваня сказал: «Это я разбил окно, Коля окно не разбивал». Коля сказал «Это сделал не я и не Саша». Саша сказал: «Это сделал не я и не Ваня». А Бабушка сидела на лавочке и все видела. Она сказала, что только один мальчик оба раза сказал правду, но не назвала того, кто разбил окно. Кто же это?

В

К

0

С

0

0

Слова В

В

1

1

1

0

0

┐ К

Слова К

0

0

1

┐ К

0

1

Слова С

1

┐ С

1

0

1

┐ С

0

0

1

┐ В

1

1

1

1

1

1

0

Ответ: разбил Коля

РТ. № 89 Дело о вымогательстве В вымогательстве подозреваются Брагин, Кургин и лиходеев. Каждый их них дол следующие показания. Брагин: «Я не участвовал в вымогательстве. Это делал Лиходеев». Лиходеев: «Я не виноват, но и Кургин тут ни причём». Кургин: «Лиходеев не виновен. Вымогательство совершал Брагин». Следствием точно установлено, что вымогали двое, кроме того, подозреваемые путались в показаниях и каждый из них не дал полностью правдивых показаний. Кто же совершал вымогательства?

Задачи другого типа

В условии приводится несколько двойных утверждений, в которых одно утверждение истинно, а другое ложно. Результат – расстановка участников по местам.

Пример:

Перед началом турнира болельщики высказали следующие предположения по поводу своих кумиров:

А. Макс победит, Билл – второй.

Б. Билл – третий, Ник – первый.

В. Макс – последний, а первый – Джон.

Когда соревнования закончились, оказалось, что каждый болельщик был прав только в одном из своих прогнозов. Какое место на турнире заняли Джон, Билл, Ник, Макс?

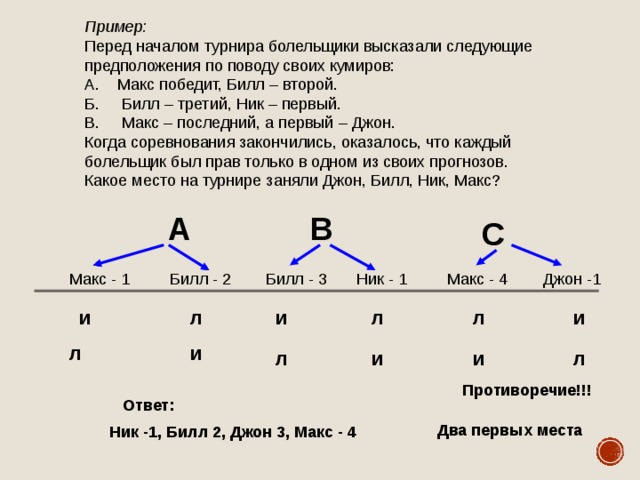
Пример:

Перед началом турнира болельщики высказали следующие предположения по поводу своих кумиров:

А. Макс победит, Билл – второй.

Б. Билл – третий, Ник – первый.

В. Макс – последний, а первый – Джон.

Когда соревнования закончились, оказалось, что каждый болельщик был прав только в одном из своих прогнозов. Какое место на турнире заняли Джон, Билл, Ник, Макс?

А

В

С

Билл - 3

Билл - 2

Макс - 1

Джон -1

Ник - 1

Макс - 4

И

Л

И

Л

И

Л

И

Л

И

Л

Л

И

Противоречие!!!

Ответ:

Ник -1, Билл 2, Джон 3, Макс - 4

Два первых места

Задача. Четыре студента Денис, Коля, Рустам и Соня по

итогам сессии стали лучшими, но пока неизвестно кто

на каком месте находится.

Сокурсники высказали предположения:

• Первым будет Денис, вторым Коля; Вторым будет Рустам, четвертой Соня; Денис будет вторым, Соня – третьей.
• Первым будет Денис, вторым Коля;
• Вторым будет Рустам, четвертой Соня;
• Денис будет вторым, Соня – третьей.

Оказалось, что в каждом предположении одно

высказывание было ложным, другое истинным.

Как распределились места?

В ответе укажите буквы имен студентов.

Задание

Один из братьев поставил на скатерть кляксу.

- Кто запачкал скатерть? – спросила бабушка.

- Витя не ставил кляксу, - сказал Алёша, - это сделал Боря.

- Ну а ты что скажешь? – спросила бабушка Борю.

• Это Витя поставил кляксу, - сказал Боря, - а Алёша

не пачкал скатерть.

- Я знаю, что Боря не мог этого сделать.– сказал Витя.

Оказалось, что два мальчика сказали правду, а один сказал

неправду. Кто поставил на скатерть кляксу?

Задание

Один из братьев поставил на скатерть кляксу.

- Кто запачкал скатерть? – спросила бабушка.

- Витя не ставил кляксу, - сказал Алёша, - это сделал Боря.

- Ну а ты что скажешь? – спросила бабушка Борю.

- Это Витя поставил кляксу, - сказал Боря, - а Алёша не пачкал скатерть.

- Так я и знала, что вы друг на друга сваливать будете, - рассердилась бабушка. – Ну а каков твой ответ? – спросила она Витю.

- Не сердись, бабуля! Я знаю, что Боря не мог этого сделать.– сказал Витя.

Оказалось, что два мальчика сказали правду, а один сказал неправду. Кто поставил на скатерть кляксу?

Решение: формализуем высказывания

Так как, справедливыми могут только одна пара высказываний,

то конечное логическое выражение будет иметь вид:

Ответ: Витя.

Задание на дом:

§1.3.3; №16 РТ.: №93