Получите свидетельство
Вход
0 б) Д в) Д = 0, то уравнение имеет единственное решение х=- " width="640"
Решение квадратных уравнений с параметрами
(1)
А, В, С- выражения, зависящие от параметров
Схема исследования уравнения
- Если А=0, то В ∙х + с = 0 , х =
- Если А≠0, то находим дискриминант
а) Д 0
б) Д
в) Д = 0, то уравнение имеет единственное решение х=-
При каких значениях параметра а уравнение
имеет 1 корень (совпадающие корни) ?
Пример 1.
Решение .
Найдем все значения параметра а, при которых уравнение имеет 1 корень D = 0 .
= 0
Ответ.
0 , а≠1 4(5а+4) ) 0 , а -4/5. б) Д а -4/5 в) Д = 0, а =-4/5 Ответ: если а -4/5 и а≠1 , то два различных корня, если а -4/5, то нет корней, если а =-4/5, то два равных корня. " width="640"
Найти все значения параметра а, для которых уравнение
а) имеет 2 различных корня;
б) не имеет корней;
в) имеет 2 равных корня.
Пример 1.
Решение.
Данное уравнение по условию является квадратным, поэтому а-1 ≠0.
Найдем дискриминант уравнения
а) Д 0 , а≠1 4(5а+4) ) 0 ,
а -4/5.
б) Д а -4/5
в) Д = 0, а =-4/5
Ответ: если а -4/5 и а≠1 , то два различных корня,
если а -4/5, то нет корней,
если а =-4/5, то два равных корня.
Пример 2.
При каких значениях параметра а уравнение
не имеет решений ?
Решение.
- а = 2, а = -1
При а=2, 3х+1=0, х = - 1/3
при а = -1, , не имеет решений.
2) а 2 , а -1
В данном случае уравнение является квадратным и не имеет решений, если дискриминант меньше нуля
Д =
Д 0
Теперь с учетом первого случая получаем
Ответ:
Пример 3.
При каких значениях параметра а уравнение
имеет единственное решение ?
Пример 3.
При каких значениях параметра а уравнение
имеет единственное решение ?
Решение.
По условию задачи уравнение необязательно является квадратным, поэтому рассмотрим два случая
1)
Если а = -6,то -12х+1=0,
х = 1/12.
2) Если а ≠ -6, то квадратное уравнение имеет единственное решение, если Д =0
Ответ: при
Пример 4.
Для всех значений параметра а решить уравнение
2 , то -нет решений а и , то " width="640"
Пример 4.
Для всех значений параметра а уравнение
Решение.
1) Если а = 1,то уравнение имеет вид -2х+3=0, х = 3/2.
2) Если а ≠ 1. Найдем дискриминант уравнения
В зависимости от значения Д возможны случаи.
а) Уравнение не имеет корней
б) тогда
в)
Ответ: если а=1,то х = 3/2.
а=2, то х=2,
а 2 , то -нет решений
а и , то
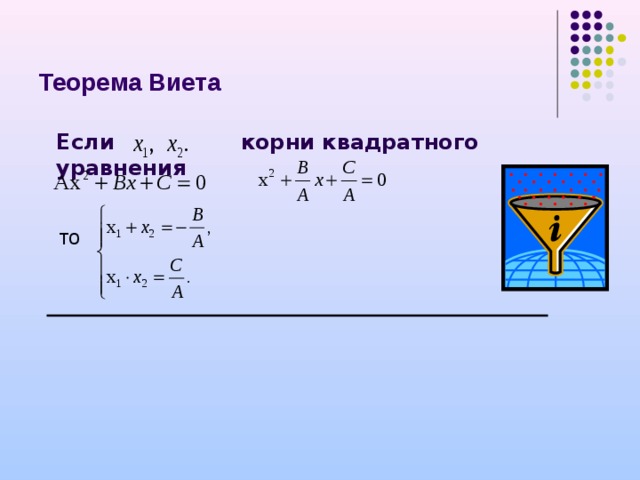
Теорема Виета
Если корни квадратного уравнения
то
Равенства, которые необходимо знать
Если корни квадратного уравнения
, то
Пример 1 .
Найти сумму и произведение корней уравнения
Пример 1.
Найти сумму и произведение корней уравнения
Решение.
1) Проверка: имеет ли уравнение действительные корни ?
Уравнение имеет действительные корни .
2 ) Нахождение суммы и произведения корней уравнения с использованием теоремы Виета.
Пример 2.
Найти сумму и произведение корней уравнения
Пример 2.
Найти сумму и произведение корней уравнения
Решение.
Проверка: имеет ли уравнение действительные корни ?
Уравнение не имеет действительных корней .
Ответ. Уравнение не имеет действительных корней.
Пример 3.
При каких значениях параметра а произведение
корней уравнения равно 10 ?
Пример 3.
При каких значениях параметра а произведение
корней уравнения равно 10 ?
Решение.
1) Найдем все значения параметра а, при которых уравнение имеет действительные решения.
Д≥ 0
2 ) По теореме Виета произведение корней уравнения
равно 10, если
Решение системы:
Ответ :
Пример 4
Не решая уравнения
найти , где
корни уравнения
Ответ:
Пример 5.
При каких значениях параметра а сумма квадратов корней уравнения равна 4?
Ответ: при а = 0
Пример 6
При каких значениях параметра р разность корней уравнения
равна 9.
Ответ : при р = -81и р =1
Применение теоремы Виета при исследовании знаков корней квадратного трехчлена
- Уравнение имеет корни одного знака, если
- Уравнение имеет положительные корни, если
- Уравнение имеет отрицательные корни, если
- Уравнение имеет корни разных знаков, если
0 2 ) Уравнение имеет корни разных знаков, если Решение системы : Ответ: " width="640"
Пример 1.
При каких значениях параметра а уравнение
имеет корни разных знаков ?
Решение.
1 ) Найдем все значения параметра а, при которых уравнение имеет действительные решения.
,Д 0
2 ) Уравнение имеет корни разных знаков, если
Решение системы :
Ответ:
Пример 2.
При каких значениях параметра а уравнение
имеет
а) корни разных знаков;
б) корни одного знака;
в) положительные корни
Решение.
По формулам Виета
а) исходное уравнение имеет корни разных знаков, если выполняется условие
б ) исходное уравнение имеет корни одного знака, если выполняется условие
в) ) исходное уравнение имеет положительные корни, если выполняется условие
Ответ: если ,то уравнение имеет корни разных знаков,
если , то корни – одного знака;
если , то положительные корни.
Решение квадратных уравнений с параметрами (976 KB)
0
2073
59
Нравится
0
