Цели заседания:
- повторить алгоритм решения линейных и квадратных уравнений;
- познакомить учащихся с решением уравнений 3 степени;
- способствовать развитию навыка решения уравнений высших степеней.
- развивать индивидуальные способности учащихся, исследовательскую культуру.
Начинаем заседание математического клуба. Сегодня в нем участвуют учащиеся 10 класса, 9 класса и наши гости - пятиклассники.
Алгебра держится на 4х китах: уравнение, число, тождество, функция. Отделить одного от другого невозможно - они «плавают» вместе. Но все же сегодня мы присмотримся к первому киту алгебры - уравнениям.
Уравнения решают с незапамятных времен, древние ученые владели приемами решения задач с неизвестными величинами. Сочинение Аль-Хорезми, жившем в IX веке, стало отправной точкой в становлении науки о решении уравнений.
Знакомство школьников с уравнениями происходит тоже достаточно рано, еще в начальной школе. Вы, члены нашего клуба, будучи 5-классниками, как и наши гости, умели отвечать на вопросы: «Что такое уравнение?», «Что значит решить уравнение?». Слушаем ответы пятиклассников.
Мир уравнений велик, их можно классифицировать по разным признакам, но ответы на заданные вопросы принципиально не отличаются, говорим ли мы о рациональном уравнении, показательном или тригонометрическом. То, что заложено в 5 классе, работает и в 10.
Несмотря на то, что пятиклассники уже решают уравнения, составляют их по тексту задачи, они все-таки многие задачи решают арифметическим способом.
Возьмем, например, классическую задачу о кроликах и фазанах (при подготовке к олимпиадам мы решали их в разных интерпретациях)
Пусть в клетке 15 животных (кролики и фазаны), а лапок у них 42. Сколько кроликов и сколько фазанов в клетке?
Решение:
15*2=30 (лапок) было бы, если все 15 животных – фазаны.
42-30=12(лапок) не достает, а добавить 2 лапки можно, заменив фазана- на кролика.
12:2=6(замен) нужно сделать, а значит в клетке 6 кроликов.
15-6=9(фазанов)
А как решили бы эту задачу те, кто не первый год изучает алгебру?
Пусть в клетке х кроликов и (15-х) фазанов, тогда 4х лапок у кроликов и 2(15-х) лапок у фазанов. Т.к. всего лапок 42, то 4х +2(15-х), 2х=12, х = 6, 15-х = 9.
Можно ввести 2 переменные и составить систему двух уравнений.
Чем труден язык арифметического решения?
Надо все время помнить условие, помнить, как связаны, входящие в условие числа. Все время понимать смысл выполняемых вычислений.
А при алгебраическом решении? Труднее всего составить уравнение (для этого надо хорошо понять условие и суметь записать его в виде равенства выражений, содержащих буквы), но зато потом надо не столько думать, сколько выполнять алгоритм.
Конечно, нужно основательно поработать, чтобы понять и выучить этот алгоритм.
Дадим задание 5-классникам и подумаем, алгоритмы решения каких уравнений вам уже известны из школьных уроков? Повторим их (значение этих алгоритмов поможет и при решении более сложных уравнений).
Самым первым был алгоритм решения линейного уравнения ах + в = 0. Повторяем его.
Линейные уравнения - самые простые из тех, что мы решаем.
Но надо помнить, что главной задачей в решении любого уравнения, является сведение его к простейшим, поэтому их надо решать без ошибок. Да и линейное уравнение можно усложнить, если ввести в него модуль, параметр.
Решим:
1) |9-4х| = 1
9-4x=1 9-4x=-1
-4x=-8 -4x=-10
x=2 x=2.5
Ответ:2,2.5
2)|x+4|+|x-3|=7
x=-4 x=3
1. x<-4
-x-4-x+3=7
-2x-1=7
-2x=8
x=-4 не удовлетворяет условию x<-4
2.-4≤x≤3
x+4+3-x=7
7=7 x Є [-4;3]
3.x+4+x-3=7
2x=6
x=3 не удовлетворяет условию x>3
Ответ [-4;3]
Рассматривается алгоритм решения квадратного уравнения (смотри архив)
6) Как решить неполное уравнение?
Решаем устно:
1)х2+9х+20=0 -4 и-5
2)y2 -17у+30=0 15 и 2
3)х2-х-12=0 4 и-3
4)x2+x-30=0 -6 и 5
5)х2-21х+20=0 1 и 20
Каким свойством обладают уравнения:
1)х2 +1999х - 2000=0 1 и -2000
2)2x2 ![]() -Зх+1=0 1 и 1/2
-Зх+1=0 1 и 1/2
3)127х2+123х-250=0 1 и -250/127
Как ни много способов решения квадратных уравнений, а открыть что-то новое можно и здесь.
Расскажем еще об одном способе решения квадратных уравнений:
aх2+вх+с=0
умножим на а обе части уравнения:
(ах)2 +в(ах)+са=0
(ах)=у
y2+ву+са=0
x1=y1/a
x2=y2/a
1)2х2-5х+3=0
y1 =2 у2=3
x1=1 x2=1.5
В архиве ещё пять уравнений.
Решим квадратное уравнение с параметром из олимпиады:
x2+2х-3|х+1|+3=0
1. если х >-1 х2 +2х-3(х+1)+3=0
x2 +2х-3х-3+3=0
x2 - х=0
х=0 или х=1
2. если х<-1 х2 +2х-3(-х-1)+3=0
x2 +2х+3х+3+3=0
x2+5х+6=0
x1=-2 x2=-3
Теперь переходим к решению уравнений III степени (кубическим уравнениям)
Приводятся исторические сведения и способы решения уравнения.
Какой план практического решения уравнения З степени
1) Найти делители свободного члена. Проверить есть ли среди них корни
2) Если корень а найден, делить многочлен на (х-а), понижать его степень
3) Если целых корней нет, можно попробовать методом неопределенных. коэффициентов.
4) Не забывать об основных приемах решения :
а) разложить на множители левую часть уравнения
б) ввести новую переменную
Дальше в архиве примеры кубических уравнений.
Для решения уравнений 4 степени важно знать два красивых искусственных приема
для решения биквадратного уравнения
для решения возвратного уравнения
Решение некоторых уравнений может оказаться достаточно простым, если при их решении воспользоваться свойством монотонности функции:
x5 +3х - 4=0
х=1
Перед вами список уравнений. Проанализировать, указать способ решения.
27х3+9х2-48х+20=0
у3+.у2-16у+20=0
x3+8=3х|х+2|
Литература
1. М.Л. Галицкий и др. “Сборник задач по алгебре для 8 – 9 кл.” М.: Просвещение, 1995 г.
2. Л.М. Поповок “1000 проблемных задач по математике”. М.: Просвещение, 1995 г.
3. Л.Ф. Пичурин “За страницами учебника алгебры”. М.: Просвещение, 1995 г.
4. Н.Я. Виленкин и др. “За страницами учебника математики”. М.: Просвещение, 1996 г.

 Получите свидетельство
Получите свидетельство Вход
Вход


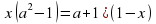
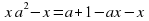
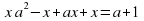
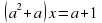
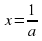
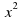 + вх + с = 0
+ вх + с = 0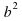 -4ас
-4ас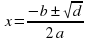
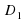 =
=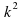 -ас
-ас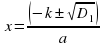
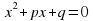
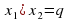
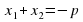
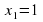
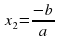

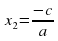
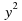 -17у+30=0 15 и 2
-17у+30=0 15 и 2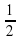
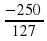
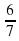
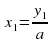









 Решение уравнений (34.34 КB)
Решение уравнений (34.34 КB)
 0
0 2160
2160 161
161 Нравится
0
Нравится
0







