Цели урока:
Образовательные:
- Познакомить обучающихся с нестандартными методами решения тригонометрических уравнений.
- Научиться решать тригонометрические уравнения различными методами.
Развивающие:
- Развитие математического кругозора, мышления и речи, внимания и памяти.
Воспитательные:
- Привитие интереса к математике.
- Активность, мобильность, умение общаться.
Тип урока: Комбинированный.
Оборудование: ноутбук, проектор, экран, презентация, карточки для самостоятельной работы, лист самооценки.
План
-
Организационный момент.
- Приветствие.
- Тема урока:
- Цель урока:
- Мотивация учебной деятельности. (Презентация) (Слайд 3-6)
«Тригонометрия” происходит от греческого слова τριγουο треугольник и греческого μετρειν измерять, т.е. означает измерение треугольников. Тригонометрия - это раздел математики, в котором изучаются тригонометрические функции и их приложения к геометрии.
- Одной из наиболее важных тем тригонометрии является решение тригонометрических уравнений, с которыми мы познакомились в этом учебном году. Эта тема очень актуальна и важна, т.к. входит в вопросы переводного экзамена в 10 кл. и широко представлена на ЕГЭ в 11 кл.
- Актуализация опорных знаний (Слайд 7-12)
(Получают листы самооценки)
1. Для успешного усвоения новой темы вы должны уметь решать простейшие тригонометрические уравнения вида: cos t = а, а≤1; sin t = а, а≤1, tg t = а,
ctg t = а
Назовите формулы корней для уравнения вида cos t = а , а≤1
Назовите формулы корней для уравнения вида sin t = а, а≤1
Назовите формулы корней для уравнения вида tg t = а
Назовите формулы корней для уравнения вида ctg t = а
3. Для успешного решения сложных тригонометрических уравнений необходимо знать алгоритм решения квадратного уравнения. и теорему Виета.
- Изучение нового материала. (Слайд 13-18)
Сегодня на уроке мы рассмотрим основные методы решения сложных тригонометрических уравнений.
1. Метод приведение к простейшим тригонометрическим уравнениям.
Пример.
2 cos(3x – π/4) = -√2.
Решение.
cos(3x – π/4) = -√2/2.
3x – π/4 = ±(π – π/4) + 2πn, n Є Z;
3x – π/4 = ±3π/4 + 2πn, n Є Z.
3x = ±3π/4 + π/4 + 2πn, n Є Z;
x = ±π/4 + π/12 + 2πn/3, n Є Z.
Ответ: ±π/4 + π/12 + 2πn/3, n Є Z.
Сформулируйте алгоритм решения уравнений методом приведения к простейшим тригонометрическим уравнениям:
1. Выразить тригонометрическую функцию через известные компоненты.
2. Найти аргумент функции по формулам:
3. Найти неизвестную переменную.
2. Метод введения новой переменной.
Пример.
2 cos 2 x – cos x – 1 = 0
Решение:
t =cos x
2t2 – t -1 = 0
D = 9
t1 = 1 t2 = 1/2
cos x = 1 cos x = 1/2
Ответ: x= 2πn, n Є Z x=π/3 +2πn,, n Є Z.
Cформулируйте алгоритм решения уравнений методом введения новой переменной.
1. Привести уравнение к алгебраическому виду относительно одной из тригонометрических функций.
2. Обозначить полученную функцию переменной t .
3. Записать и решить полученное алгебраическое уравнение.
4. Сделать обратную замену.
5. Решить простейшее тригонометрическое уравнение.
3. Метод понижения порядка уравнения.
Формулы понижения степени:
sin2 x = 1/2 · (1 – cos 2x);
cos2 x = 1/2 · (1 + cos 2x);
tg2 x = (1 – cos 2x) / (1 + cos 2x).
Пример.
cos 2x + cos2 x = 5/4.
Решение.
1) cos 2x + 1/2 · (1 + cos 2x) = 5/4.
2) cos 2x + 1/2 + 1/2 · cos 2x = 5/4;
3/2 · cos 2x = 3/4;
cos 2x = 1/2;
2x = ±π/3 + 2πn, n Є Z;
x = ±π/6 + πn, n Є Z.
Ответ: x = ±π/6 + πn, n Є Z.
Сформулируйте алгоритм решения уравнений методом введения новой переменной.
1. Заменить данное уравнение линейным, используя для этого формулы понижения степени:
2. Решить полученное уравнение с помощью методов I и II.
4. Приведение уравнения к виду tg x =a
Однородные уравнения.
Пример.
5sin2 x + 3sin x · cos x – 4 = 0.
Решение.
1) 5sin2 x + 3sin x · cos x – 4(sin2 x + cos2 x) = 0;
5sin2 x + 3sin x · cos x – 4sin² x – 4cos2 x = 0;
sin2 x + 3sin x · cos x – 4cos2 x = 0/cos2 x ≠ 0.
2) tg2 x + 3tg x – 4 = 0.
3) Пусть tg x = t, тогда
t2 + 3t – 4 = 0;
t = 1 или t = -4, значит
tg x = 1 или tg x = -4.
Из первого уравнения x = π/4 + πn, n Є Z; из второго уравнения x = -arctg 4 + πk, k Є Z.
Ответ: x = π/4 + πn, n Є Z; x = -arctg 4 + πk, k Є Z.
Сформулируйте алгоритм решения уравнений методом приведения к виду
tg x =a
1. Привести данное уравнение к виду
a) a sin x + b cos x = 0 (однородное уравнение первой степени)
или к виду
б) a sin2 x + b sin x · cos x + c cos2 x = 0 (однородное уравнение второй степени).
2. Разделить обе части уравнения на
а) cos x ≠ 0;
б) cos2 x ≠ 0;
и получить уравнение относительно tg x:
а) a tg x + b = 0;
б) a tg2 x + b tg x + c = 0.
3. Решить уравнение известными способами.
5. Разложение на множители.
Алгоритм решения:
1. Используя всевозможные тригонометрические формулы, привести данное уравнение к уравнению, решаемому методами I, II, III, IV.
2. Решить полученное уравнение известными методами.
Пример.
sin x + sin 2x + sin 3x = 0.
Решение.
1) (sin x + sin 3x) + sin 2x = 0;
2sin 2x · cos x + sin 2x = 0.
2) sin 2x · (2cos x + 1) = 0;
sin 2x = 0 или 2cos x + 1 = 0;
Из первого уравнения 2x = π/2 + πn, n Є Z; из второго уравнения cos x = -1/2.
Имеем х = π/4 + πn/2, n Є Z; из второго уравнения x = ±(π – π/3) + 2πk, k Є Z.
В итоге х = π/4 + πn/2, n Є Z; x = ±2π/3 + 2πk, k Є Z.
Ответ: х = π/4 + πn/2, n Є Z; x = ±2π/3 + 2πk, k Є Z.
V. Домашнее задание.
Самостоятельная работа (находится в архиве)

 Получите свидетельство
Получите свидетельство Вход
Вход


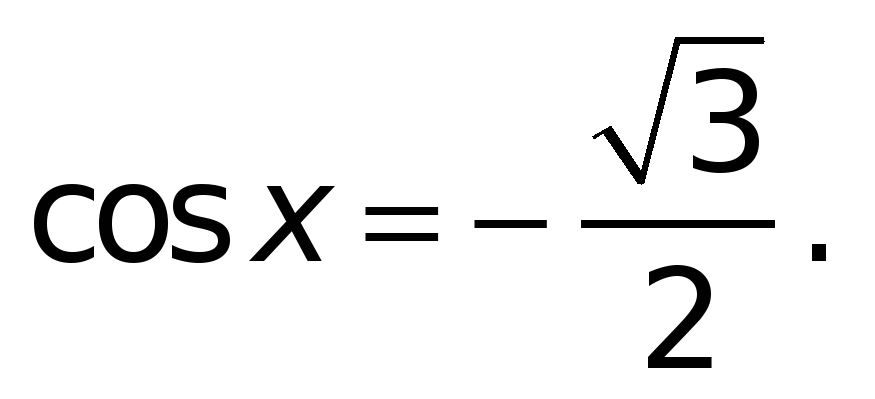 б)
б) 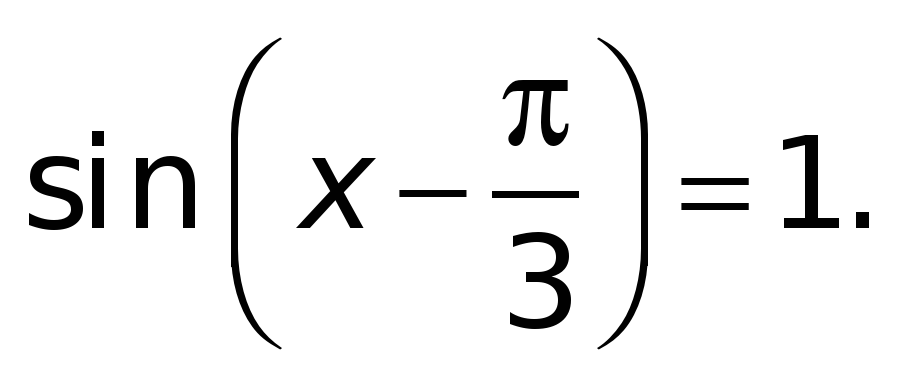 в)
в) 








 Методы решения тригонометрических уравнений (80.5 КB)
Методы решения тригонометрических уравнений (80.5 КB)
 3
3 2311
2311 441
441 Нравится
0
Нравится
0



