Долгорукова Т.Ф.
Тема: Решение тригонометрических уравнений.
Тип урока: урок-суд
Цель: - способствовать формированию умений решать тригонометрические уравнения;
- способствовать развитию навыка самостоятельности и творческого поиска;
- способствовать развитию навыка самоконтроля;
способствовать развитию поисковой и познавательной активности.
Средства: готовые заранее рисунки, схемы и таблицы, мультимедиа.
Ход урока:
Подготовка. В актовом зале развесить плакаты с изображениями тригонометрических уравнений, расположить судейский стол, кафедра, где лежит большая книга для принесения клятвы. На одной половине сцены – обвинители, на другой – обвиняемые. Каждый участник заранее готовит свою речь и костюм.
«Суд над тригонометрическими уравнениями» - это даже не игра, а театрализованное представление.
Действующие лица: корреспондент, судьи, секретарь, прокурор, адвокат, свидетели.
Перед началом суда корреспондент берет у присутствующих интервью.
Корреспондент. Добрый день дамы и господа! Мы ведем репортаж из зала заседаний.
Я корреспондент журнала "Математика в школе". Мне хотелось бы задать вам несколько вопросов:
- Какое уравнение называется тригонометрическим?
- Что вы знаете о тригонометрических уравнениях?
- Какие методы решения тригонометрических уравнений вы знаете?
- Что вы можете сказать о таком методе решения тригонометрических уравнений, как замена неизвестной новой переменной?
- Что вы можете сказать о таком методе решения тригонометрических уравнений, как использование ограниченности функции?
- Что вы можете сказать о таком методе решения тригонометрических уравнений, как графический метод?
- Применение тригонометрических уравнений?
- Ваше мнение, в чем могут быть виновны тригонометрические уравнения?
- Чем завершится сегодняшнее заседание?
Секретарь. Встать, суд идет!
Судья. Прошу всех садиться. Сегодня слушается дело об обвинении тригонометрических уравнений, в их ненужности и непригодности, в излишней заграможденности ими школьной программы. Слово предоставляется прокурору.
Прокурор. Я представляю интересы группы школьников, которые обвиняют тригонометрические уравнения в ненужности. Предлагаю провести небольшое расследование и рассмотреть вещественные доказательства подтверждающие невиновность того, что они далеки от реальности, в непонятности и запутанности.
Адвокат. Протестую, Ваша честь! Я считаю выдвинутые обвинения необоснованными, так как следствие не окончено. Предлагаю провести небольшое расследование и рассмотреть вещественные доказательства, подтверждающие невиновность моего подзащитного.
Судья. Прошу предъявить необходимые доказательства.
Адвокат. Разрешите, Ваша честь! Я предлагаю для сидящих в зале, рассмотреть способы решения тригонометрических уравнений.
Прокурор. Это ни к чему не приведет, только займет время.
Адвокат. Я предлагаю поручить следствию, что это интересно каждому школьнику, кто любит математику.
Судья. Есть возражения у обвиняемых?
Прокурор. Возражений нет.
Адвокат. Прошу следователя поручить задание и приступить к его решению.
Судья. Прошу секретаря раздать сидящим в зале условия задач, которые должны быть решены во время слушания свидетелей. А обвиняемый расскажет о способах решения тригонометрического уравнения.
Обвиняемый. Я знаю 11 способов решения тригонометрических уравнений, из которых 4 нестандартных:
1) разложением на множители;
2) преобразование тригонометрических функций в сумму;
3) применение формул понижения степени;
4) применение формул тройного аргумента;
5) домножение на конкретную тригонометрическую функцию;
6) сведение к алгебраическому уравнению;
7) универсальная тригонометрическая подстановка;
8) метод симметрии;
9)использование ограниченности функции;
10) функциональный метод решения;
11) решение исследованием функции.
Я предлагаю рассмотреть последние 3 способа решения тригонометрических уравнения. И думаю, что свидетели меня поддержат.
(3 свидетелей выступят в защиту, они по очереди покажут решения тригонометрических уравнений: использование ограниченности функции, функциональный метод решения, решение исследованием функции)
Судья. Этого не достаточно. Защита, предъявите суду ваши доказательства и свидетелей, подтверждающих невиновность подсудимой.
Адвокат. Вызывается свидетель: Свидетелю дается задание применить метод ограниченности функции при решении уравнений: а) 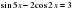 ; б)
; б) 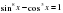 ; в)
; в) 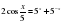 ; г)
; г) 
Свидетель. (Показывает, комментируя, решение данных заданий на доске).
а) Решить уравнение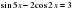 .
.
Решение.Поскольку 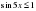 ,
, 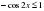 , то левая часть не превосходит
, то левая часть не превосходит 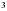 и равна
и равна 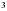 , если
, если 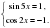
Для нахождения значений  , удовлетворяющих обоим уравнениям, поступим следующим образом. Решим одно из них, затем среди найденных значений отберем те, которые удовлетворяют и другому.
, удовлетворяющих обоим уравнениям, поступим следующим образом. Решим одно из них, затем среди найденных значений отберем те, которые удовлетворяют и другому.
Начнем со второго: 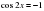 ,
, 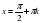 . Тогда
. Тогда 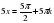 ,
, 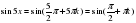 .
.
Понятно, что лишь для четных 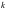 будет
будет 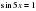 .
.
Ответ. 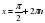 .
.
б) Решить уравнение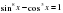 .
.
Решение.Воспользуемся свойством показательной функции: 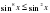 ,
, 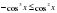 .
.
Сложив почленно эти неравенства будем иметь:
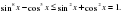
Следовательно левая часть данного уравнения равна 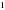 тогда и только тогда, когда выполняются два равенства:
тогда и только тогда, когда выполняются два равенства:
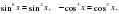
т. е. 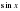 может принимать значения
может принимать значения  ,
,  ,
, 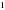 , а
, а  может принимать значения
может принимать значения  ,
,  .
.
Ответ.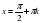 ,
,  .
.
в) Решить уравнение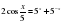 .
.
Решение. ,
,  . Следовательно,
. Следовательно,  .
.
Ответ. .
.
г) Решить уравнение
Решение.Обозначим  , тогда из определения обратной тригонометрической функции
, тогда из определения обратной тригонометрической функции  имеем
имеем  и
и  .
.
Так как  , то из начального уравнения следует неравенство
, то из начального уравнения следует неравенство  , т.е.
, т.е.  . Поскольку
. Поскольку  и
и  , то
, то  и
и  . Однако
. Однако  и поэтому
и поэтому  .
.
Если  и
и  , то
, то  . Так как ранее было установлено, что
. Так как ранее было установлено, что  , то
, то  .
.
Ответ.  ,
,  .
.
Прокурор. У кого имеются вопросы? Если нет вопросов, заслушиваем следующего свидетеля.
Свидетель. Я, покажу, как решаются задания, используя функциональный метод решения.
Задание 1. Решить уравнение
Решение.Преобразуем исходное уравнение к виду
и решим его как квадратное относительно  . Тогда получим,
. Тогда получим,

Решим первое уравнение совокупности. Учтя ограниченность функции  , приходим к выводу, что уравнение может иметь корень только на отрезке
, приходим к выводу, что уравнение может иметь корень только на отрезке  . На этом промежутке функция
. На этом промежутке функция  возрастает, а функция
возрастает, а функция  убывает. Следовательно, если это уравнение имеет корень, то он единственный. Подбором находим
убывает. Следовательно, если это уравнение имеет корень, то он единственный. Подбором находим  .
.
Ответ. .
.
Задание 2. Решить уравнение
Решение.Пусть  ,
,  и
и  , тогда исходное уравнение можно записать в виде функционального уравнения
, тогда исходное уравнение можно записать в виде функционального уравнения  . Поскольку
. Поскольку  функция нечетная, то
функция нечетная, то  . В таком случае получаем уравнение
. В таком случае получаем уравнение  .
.
Так как  ,
,  и
и  монотонна на
монотонна на  , то уравнение
, то уравнение  равносильно уравнению
равносильно уравнению  , т.е.
, т.е.  , которое имеет единственный корень
, которое имеет единственный корень  .
.
Ответ. .
.
Задание 3.Решить уравнение .
.
Решение. На основании теоремы о производной сложной функции ясно, что функция  убывающая (функция
убывающая (функция  убывающая,
убывающая,  возрастающая,
возрастающая,  убывающая). Отсюда понятно, что функция
убывающая). Отсюда понятно, что функция  определенная на
определенная на  , убывающая. Поэтому данное уравнение имеет не более одного корня. Так как
, убывающая. Поэтому данное уравнение имеет не более одного корня. Так как  , то
, то
Ответ. .
.
Судья. Есть ли вопросы у присутствующих?
Судья. И так, мы пока не видим необходимости тригонометрических уравнений в алгебре старших классов. Поэтому я могу попросить исключить данную тему из школьной программы.
Прокурор. Да, действительно доводы не достаточны.
Судья. Слово предоставляется адвокату.
Адвокат. Граждане судьи! По вышеуказанным заданиям нельзя считать ненужности тригонометрического уравнения, но на их основе решаются многие задания в 9, 10, 11 классах. Поэтому прошу вынести оправдательный приговор и продолжить изучение тригонометрического уравнения в школе.
Судья. Слово предоставляется подсудимой.
Тригонометрическое уравнение. Я имею вид 
 , зная как меня решать мы, можем без труда вычислить любой угол, а так же знание меня позволит проводить измерения там, где их невозможно произвести сравнением с эталоном. Например, в астрономии, где в большинстве случаев невозможно использовать какой-либо измерительный прибор. Кроме того на основе меня основана навигация, например - GPS навигаторы активно используют тригонометрические вычисления и решают тригонометрические уравнения для определения своих координат.
, зная как меня решать мы, можем без труда вычислить любой угол, а так же знание меня позволит проводить измерения там, где их невозможно произвести сравнением с эталоном. Например, в астрономии, где в большинстве случаев невозможно использовать какой-либо измерительный прибор. Кроме того на основе меня основана навигация, например - GPS навигаторы активно используют тригонометрические вычисления и решают тригонометрические уравнения для определения своих координат.
Зная правила построения графиков функций  и
и  можно решать задачи типа №10.9 и 10.18 из учебника «Алгебра» под редакцией Никольского С.М. В мое оправдание могут выступить свидетели из 10, 11 классов.
можно решать задачи типа №10.9 и 10.18 из учебника «Алгебра» под редакцией Никольского С.М. В мое оправдание могут выступить свидетели из 10, 11 классов.
Судья. Слово предоставляется свидетелю из 10 класса.
Свидетель (ученик 10 класса). Да, я считаю, что тригонометрическое уравнение важно в изучении алгебры в старших классах, в особенности при решении таких задач из геометрии как:
а) Предположим, что требуется определить высоту АН какого-то предмета (рис).
б) Найти расстояние d от пункта А до недоступного пункта С (рис)
Судья. Если нет вопросов к свидетелю 10 класса, то продолжим.
Подсудимый. Я не считаю себя виноватой, квадратный трехчлен применяется и при решении следующих заданий. В мою защиту выступят учащиеся 11 класса, которые посещают факультативные занятия по алгебре.
Адвокат. Граждане судьи! Разрешите слово свидетелям. Они расскажут как решаются задания типа: Решить уравнение .
Судья. Слово дается свидетелю из 11 класса.
Свидетель. Имеем .
Достаточно рассмотреть три случая:
.
 .
.
 .
.
Делая замену  , получаем, что
, получаем, что  или
или  . То есть
. То есть  или
или  . Проверим, являются ли найденные значения переменной корнями. Подставляя значения переменной в уравнение, получаем, что
. Проверим, являются ли найденные значения переменной корнями. Подставляя значения переменной в уравнение, получаем, что  не подходит, тогда корнями являются значения
не подходит, тогда корнями являются значения  .
.
3. 

Делая замену  , получаем
, получаем  или
или  . Аналогично, как и при
. Аналогично, как и при  , проверкой устанавливаем, что только
, проверкой устанавливаем, что только  и
и  не являются корнями. Тогда
не являются корнями. Тогда  является корнем. Итак,
является корнем. Итак,
Ответ. При  ,
,  ;
;
Адвокат. Я также предлагаю заслушать других свидетелей.
Судья. Разрешаю. Слово следующему свидетелю.
Свидетель (ученик 11 класса) Я покажу решение следующего задания двумя способами:
а) Указать все значения параметра  , для которых уравнение
, для которых уравнение  имеет решение?
имеет решение?
Решение. Обозначим  . Исходное уравнение
. Исходное уравнение  , с учетом
, с учетом  , равносильно системе
, равносильно системе

Рассмотрим квадратное уравнение, относительно параметра 
 . Найдем дискриминант рассматриваемого уравнения
. Найдем дискриминант рассматриваемого уравнения  .
.
 , так как
, так как  и
и  , то
, то  . Поэтому последняя система равносильна
. Поэтому последняя система равносильна 
Рассмотрим функцию  . Вершина параболы – есть точка с координатами
. Вершина параболы – есть точка с координатами  . Минимум функции есть значение ординаты вершины параболы. Поэтому можем утверждать, что параметр
. Минимум функции есть значение ординаты вершины параболы. Поэтому можем утверждать, что параметр  принимает значения в отрезке
принимает значения в отрезке  на отрезке
на отрезке  .
.
Ответ.
б) Пользуясь тем, что эта задача уже была решена, рассмотрим сразу систему

Рассмотрим функцию  при
при  . Отметим, что эта функция обратима и обратной к ней является
. Отметим, что эта функция обратима и обратной к ней является  . Так как функция возрастающая, то общие точки лежат на прямой
. Так как функция возрастающая, то общие точки лежат на прямой  . Получаем
. Получаем  . Решение которой нам известно.
. Решение которой нам известно.
Ответ. .
.
Подсудимый. Как видите, применение тригонометрического уравнения обширно, и я не считаю себя виновным.
Судья. Для вынесения приговора суд удаляется на совещание.
Секретарь. Прошу всех встать.
(Суд удаляется, в перерыве звучит музыка)
Секретарь. Встать, суд идет!
Судья. На основе рассмотренных фактов суд постановляет:
- признать тригонометрическое уравнение невиновным;
- продолжить изучение тригонометрического уравнения и его применения в курсе математики;
- приговор довести до всех учителей математики и обучающихся;
- приговор вступает в силу со дня его оглашения.
Заседание суда считаю закрытым.

 Получите свидетельство
Получите свидетельство Вход
Вход



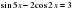 ; б)
; б) 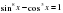 ; в)
; в) 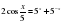 ; г)
; г) 
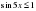 ,
, 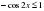 , то левая часть не превосходит
, то левая часть не превосходит 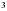 и равна
и равна 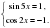
 , удовлетворяющих обоим уравнениям, поступим следующим образом. Решим одно из них, затем среди найденных значений отберем те, которые удовлетворяют и другому.
, удовлетворяющих обоим уравнениям, поступим следующим образом. Решим одно из них, затем среди найденных значений отберем те, которые удовлетворяют и другому.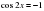 ,
, 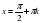 . Тогда
. Тогда 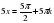 ,
, 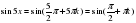 .
.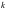 будет
будет 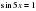 .
.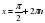 .
.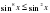 ,
, 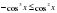 .
.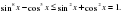
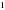 тогда и только тогда, когда выполняются два равенства:
тогда и только тогда, когда выполняются два равенства: 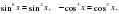
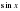 может принимать значения
может принимать значения 








 Конспект урока по математике "Решение тригонометрических уравнений" (0.26 MB)
Конспект урока по математике "Решение тригонометрических уравнений" (0.26 MB)
 0
0 541
541 73
73 Нравится
0
Нравится
0







