Цели :
- повторить свойства тригонометрических функций, знания основных тригонометрических тождеств, изучить два метода решения тригонометрических уравнений;
-развивать память, речь, логическое мышление у учащихся, развивать вычислительные навыки работы, поставить учащихся перед проблемой самостоятельного поиска способа решения тригонометрических уравнений;
-воспитывать настойчивость в приобретении знаний и умений, аккуратность оформления решений в тетрадях у учащихся.
План урока:
1.Целеполагание:
Сегодня на уроке мы с Вами будем изучать 2 метода решения тригонометрических уравнений.
2. Задание домашней работы:
А-№164(а,б), 165 (б,г)
В-№164 (а-в), 165 (а-в), 168(а,б)
3. Подготовительная работа для изучения новой темы:
а)-определить вид уравнения:
ах2+вх+с=0
ах2+вх=0
ах2+с=0
ах2 =0
какое уравнение называется квадратным?
Сколько действительных решений может иметь полное квадратное уравнение?
Уравнения какого вида называются неполными квадратными уравнениями?
Каким наиболее рациональным способом можно решить эти уравнения?
Б) Найдите область значения функций:
Y=cos x
Y=sin x
E=cos x –1
Y=3 sin x
В) на доске 2 ученика записывают решения простейших тригонометрических уравнений и их частные случаи.
1 уч- sin x =a
2 уч- cos =a
на заготовке ватмана записаны простейшие тригонометрические уравнения и их решения . Учащимся необходимо поставить соответствия с дальнейшей самопроверкой ( заготовлена учителем) – смотрите документ.
4. Введение новой темы:
Сегодня на уроке мы будем изучать 2 метода решения тригонометрических уравнений. Начнём решать тригонометрические уравнения с уже предложенного.
2sin2x+sinx-1=0
В этом уравнении 1 функция sin и один аргумент х.
Давайте подумаем как можно решить это уравнение ?
Решим это уравнение методом замены переменной.
Пусть sin x=t
2t2+t-1=0
D=9, D>0 уравнение имеет 2 действительных корня
Чем это уравнение отличается от предыдущего? (аргументом)
Будет ли другой метод решения данного уравнения?
Решим его (ученик)
8cos2 x+6sin x-3=0
В данном уравнении у нас разные функции , но одинаковые аргументы. Нам необходимо привести это уравнение к уравнению с одной функцией. Для этого воспользуемся основным тригонометрическим тождеством:
Полученное тригонометрическое уравнение мы будем решать методом замены переменной
1+cos x=-cos 2x
Уравнение имеет 1 функцию, но разные аргументы. Что мы можем использовать ( какие знания) для того, чтобы привести это уравнение к уравнению с одним аргументом?
Мы получили неполное квадратное уравнение относительно cos x. Каким наиболее рациональным способом мы можем решить данное уравнение? (вынесением общего множителя за скобки)
sin x –sin 2x=0
Уравнение имеет одну функцию , но разные аргументы, Как можно решить данное уравнение? ( с помощью формул двойного угла)
Закрепление нового материала:
Перед Вами на доске находятся уравнения. Вам необходимо распознать уравнения:
-Которые можно решить методом замены переменной;
-Уравнения, которые с помощью основных тригонометрических тождеств можно привести к уравнениям решаемым методом замены переменной;
-Неполные квадратные уравнения.
Подведение итогов урока:
-Давайте ребята вспомним, что сегодня мы изучали на уроке?
-Если уравнение имеет 1 функцию и 1 аргумент , то как мы будем решать такие уравнения?
-Если уравнение имеет 1 функцию но разные аргументы , то как мы будем решать такие уравнения?
-Если уравнение имеет разные функции и 1 аргумент , то как мы будем решать такие уравнения?
-Если уравнение неполное квадратное уравнение, то каким методом мы будем решать такие уравнения?
Самостоятельная работа учеников:
Перед вами находятся карточки , которые я вам предлагаю решить. Прощу вас начать их решение с уравнения наиболее вам понятного и не вызывавшего трудности при решении.
( Через 2-3 мин на доске 2 ученика начинают решать эти уравнения ( 1-с объяснением) , ученики у которых уравнения вызывают трудности имеют шанс ещё раз проверить правильность своего решения)
Весь материал - смотрите документ.

 Получите свидетельство
Получите свидетельство Вход
Вход




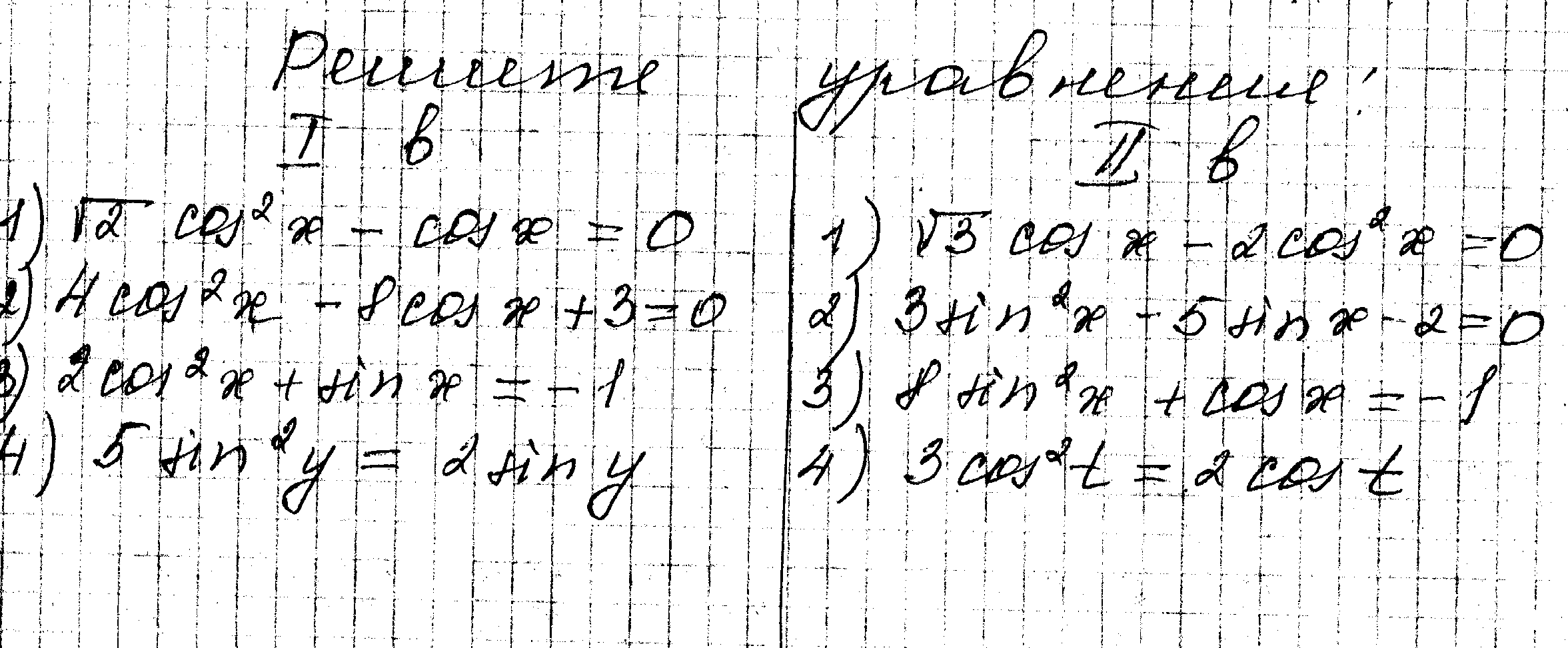
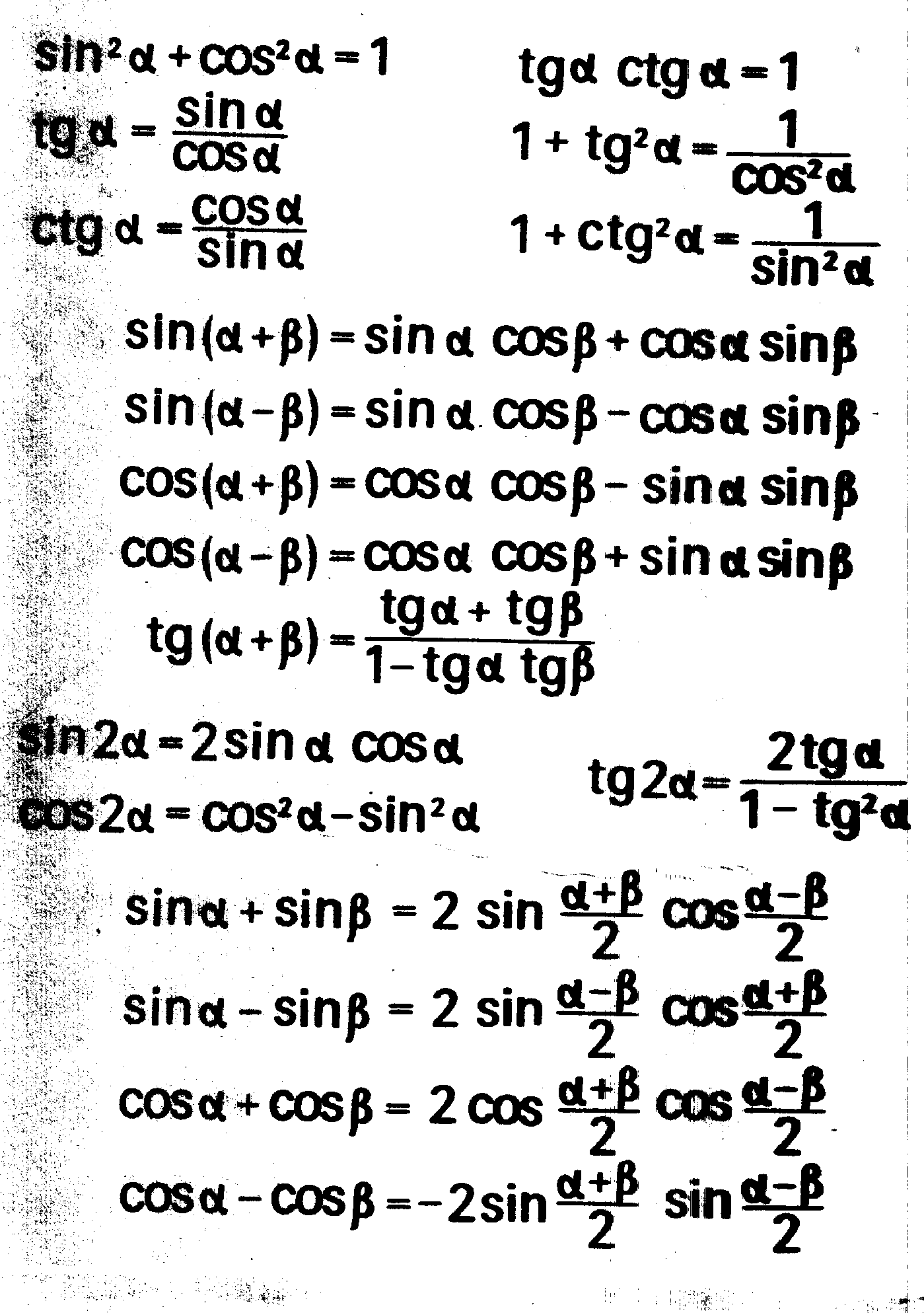









 Решение тригонометрических уравнений (урок 1) (0.18 MB)
Решение тригонометрических уравнений (урок 1) (0.18 MB)
 0
0 1134
1134 88
88 Нравится
0
Нравится
0









