Урок по математике в 10 классе (учебник Мордкович А. Г.)
Тема: «Понятие производной»
Тип урока: урок изучения нового материала
Цели: а) образовательные - ввести понятие производной, получить основные формулы дифференцирования;
б) воспитательные - воспитывать чувство ответственности и самостоятельности;
в) развивающие- развивать логическое мышление, умение применять на практике ранее полученные знания при изучении нового материала.
План урока.
I. Мотивационный этап.
II.Введение понятия:
а) геометрическая иллюстрация изменения приращения функции;
б) определение касательной к графику функции;
в) определение производной функции;
III.Контрольный этап (нахождение производных некоторых функций).
I.Задача: требуется огородить участок земли прямоугольной формы проволокой длины 100 метров так, чтобы его площадь была наибольшей.
Предложить учащимся назвать измерения прямоугольника с периметром 100 метров, иллюстрируя предложения:
600 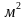
525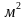
400 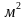
625 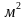
20м 15м 10м 25м
Вопросы. При каких размерах участка его площадь будет наибольшей? Существует ли прямоугольник с площадью большей, чем 625 квадратных метров? Если не существует,то как это доказать?
Учащиеся приходят к выводу, что традиционными приемами эта задача не решается. Вопрос остается открытым. Предложить учащимся вернуться к решению данной задачи позже, изучив новый раздел курса «Производная».
II. Задача: используя индуктивный метод, сформулировать определение производной функции. Этому способствует решение следующего упражнения: выразить приращение функции через приращение аргумента, найти угловой коэффициент секущей к графику функции, проходящей через точки с абсциссами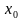 и x , дать графическую иллюстрацию.
и x , дать графическую иллюстрацию.
f(x)=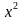 ;
; 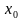 =0,5.
=0,5.
1.f(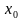 )=
)=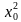 .
.
2.f(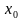 +
+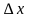 )=
)=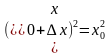 +2
+2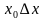 +
+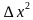
3. f=2
f=2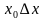 +
+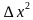
4.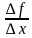 = 2
= 2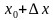
Данный алгоритм отработан на предыдущих уроках.
Дальнейшие вычисления сведены в таблицу:
| № |
|
|
|
| 1 | 0.5 | 0.5 | 1.5 |
| 2 |
| 0.3 | 1.3 |
| 3 |
| 0.2 | 1.2 |
| 4 |
| 0.1 | 1.1 |
| 5 |
| 0.01 | 1.01 |
↓ ↓
0 1
Вывод:если 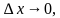 то
то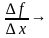 1
1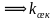 =1
=1 угловой коэффициент секущей равен 1)
Если 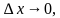 то
то 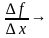 2
2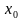 .
.
Г рафическая иллюстрация. Задание.Составить уравнение прямой с угловым коэффициентом 1 и проходящей через точку
(0.5; 0.25). Изобразить прямую в координатной плоскости. Как будут расположены данная прямая и парабола?
Решение: уравнение прямой y=kx+b, с учетом условий задания 0.25=1 0.5+b, откуда b=-0.25.
Искомая прямая y=x-0.25. По аналогии с касательной к окружности, учащиеся после построения называют данную прямую касательной. Записываем определение касательной к графику функции и производной функции в точке.
Определение. Прямая, проходящая через точку( f
)) , с отрезком которой практически сливается график функцииy=f(x) в некоторой окрестности точки
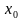 , называется касательной к графику функции в точке(
, называется касательной к графику функции в точке( f
)).
По итогам практической работы формулируем вывод: угловой коэффициент касательной к графику функции в точке( f
)) равен числу, к которому стремится отношение приращения функции в точке с абсциссой
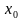 к приращению аргумента, если приращение аргумента стремится к 0, то есть
к приращению аргумента, если приращение аргумента стремится к 0, то есть А, если
0. Тогда становится доступно определение производной функции в точке
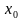 .
.
Определение. Число, к которому стремится разностное отношение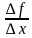 = при
= при
, если
А-«производная»
Такой порядок рассуждений готовит учащихся к осмыслению не только определения производной функции в точке, но и ее геометрического смысла.
III. Контрольный этап. Позволяет судить о степени усвоения понятия по умению записывать формулы производных конкретных функций с использованием алгоритма. Оценка работы учащихся на данном этапе - качественная. Итог-получение набора формул дифференцирования.
Это работа с функциями: f(x)=x, f(x)=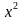 , f(x)=
, f(x)= , f(x)=
, f(x)=1/x, f(x)=С.
Пример: найти производную функции f(x)= .
1.f(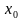 )=
)= .
2.f(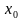 +
+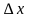 )= +3
)= +3 +3
+
3. f=3
f=3 +3
+
4.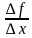 = 3
= 3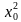 +3
+3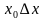 +
+ 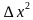
5.Если 3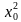
Вывод:f’(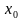 )=3
)=3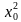 или
или )’=3
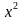
В ходе фронтальной работы получаем формулы дифференцирования: С’=0, =1,
,
( )’ =3
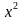 , (
, ( )’ =
, (1/x)’ = -
Задание учащимся их выучить. Итак, на данном этапе оценка деятельности учащихся качественная, выражающаяся в умении вывести формулы. На последующих занятиях, по мере изучения правил дифференцирования, формул дифференцирования тригонометрических функций, правила дифференцирования сложной функции с целью оценки и формирования умений и навыков на каждом занятии предлагаю набор тренировочных упражнений в форме диктанта. Самоконтроль, самооценка, гласность их результатов стимулируют ответственное отношение учащихся к изучению темы.
Набор заданий для самоконтроля и самооценки по теме: «Производная функции».
№1 №2 №3
(3 ) ’ (1/3
) ’ (2/
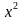 ) ’
) ’
(2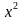 ) ’ (2/
) ’ (2/ ) ’ (4
) ’
(4/ ) ’ (3/
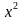 ) ’ (6
) ’ (6 ) ’
(2 (5
-1/
’ (4/
(2 ) ’ (1/
’ (
( ) ’ (4
’ (1/5
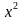 )’
)’
(1+ ’ (8+3
’ (3/
(4 ) ’ (
(1/
) ’
5’ (1/3 ((
( ) ’ (-6/

 Получите свидетельство
Получите свидетельство Вход
Вход











 Урок по теме " Понятие производной" (144.73 KB)
Урок по теме " Понятие производной" (144.73 KB)
 0
0 1470
1470 135
135 Нравится
0
Нравится
0






