Урок по геометрии в 9 классе " Решение треугольников"

Конспект открытого урока в 9 классе по теме: «Решение треугольников».

Тип урока: обобщающий

Цели:

• закрепить знания, умения и навыки учащихся по изученной теме, устранить пробелы в знаниях;

• совершенствовать навыки решения задач на применение теорем синусов и косинусов;

• освоить представление о методах измерительных работ, показать практическую направленность данной темы.

• развивать логическое мышление, способности самостоятельно решать учебные задачи;

• прививать интерес к предмету с помощью применения информационных технологий, формировать коммуникативные навыки учащихся.

Форма урока: урок-практикум.

Оборудование: интерактивная доска, компьютер.

Научить:

• определять расстояние до недоступной точки;

• определять высоту предмета;

• решать задачи на использование теоремы синусов и теоремы косинусов.

Ход урока.

Ι. Организационный момент.

Объявляется тема урока.

ΙΙ. Историческая справка (презентация).

«Все вокруг геометрия»

Почему же выбрана именно геометрия?

«Математика – царица наук» и, наверное, не каждый догадывается, что огромный толчок в развитии всей математики дала именно геометрия. Геометрия – «измеряю землю».

Почти все великие ученые древности и средних веков были выдающимися геометрами. Древнегреческий философ Платон, проводивший беседы со своими учениками в роще «Академа», откуда и пошло название «академия», одним из девизов своей школы провозгласил: «не знающие геометрии не допускаются!» Было это примерно 2400 лет тому назад. Из геометрии вышла наука, которая называется математикой.

Повторим теорию (презентация, слайды).

ΙΙΙ. Тест (обратная связь: ученики голосуют сигнальными карточками).

Тест на закрепление теоретических знаний с последующей самопроверкой и обсуждением тех заданий, по которым допущены ошибки.

1. Для треугольника АВС справедливо равенство:

а) АВ² = ВС^{2 +} АС²- 2ВС·АС· cos ВСА;

б) ВС² = АВ²+ АС² -2АВ· АС·cosАВС;

в) АС² = АВ² + ВС² – 2АВ· ВС·cosFCD.

2. Площадь треугольника МNK равна:

а) 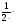МN· MK ·sin MNK;

б) 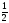·МК·NK· sin MNK;

в) 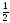·MN· NK ·sin MNK.

3. Если квадрат стороны треугольника равен сумме квадратов двух других его сторон, то эта сторона лежит против:

а) тупого угла;

б) прямого угла;

в) острого угла.

4. В треугольнике АВС известны длины сторон АВ и ВС. Чтобы найти сторону АС, необходимо знать величину:

а) угла А;

б) угла В;

в) угла С.

5. Треугольник со сторонами 5, 6 и 7 см;

а) остроугольный;

б) прямоугольный;

в) тупоугольный.

6. В треугольнике АВС A=30˚, ВС=3. Радиус описанной около ∆АВС окружности равен:

а) 1,5;

б) 2;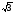

в) 3.

7. Если в треугольнике АВС А =48˚, В =72˚, то наибольшей стороной треугольника является сторона:

а) АВ;

б) АС;

в) ВС.

8. В треугольнике СDЕ:

а) СD·sin C = DЕ· sin Е;

б) СD· sin Е = DЕ·sinC;

в) СD· sin D =DE· si n E.

9. По теореме синусов:

а) Стороны треугольника обратно пропорциональны синусам противолежащих углов.

б) Стороны треугольника пропорциональны синусам противолежащих

в) Стороны треугольника пропорциональны синусам прилежащих углов.

10. В треугольнике АВС АВ = 10см, ВС =5 см. найти отношение синуса угла А к синусу угла С.

а)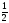; б) 5; в) 2.

IV. «Зачем нам нужен треугольник ?»

Презентация: «В мире треугольников»

V. Практическое применение теоремы косинусов и синусов.

Работа в группах.

Основы сотрудничества:

- каждый должен слушать своих товарищей;

- каждый должен принимать участие в работе;

- каждый должен просить о помощи, когда она ему нужна;

- каждый должен оказать помощь, если его об этом попросят.

Повторить виды решения треугольников (презентация).

Вопрос классу: при определении угла треугольника что лучше находить, синус или косинус? (Ответ на слайде).

Решить задачи (презентация)

Задача №1.

Футбольный мяч находится на расстоянии 23м от одной штанги ворот и 24м от другой.

Ширина ворот 7м. Найдите угол попадания мяча в ворота.

Задача №2.

Два геолога находятся на одном берегу реки на расстоянии 300м друг от друга. Один видит дерево на противоположном берегу под углом 38˚, а другой это же дерево – под углом 67˚. Найдите, на каком расстоянии от дерева находится каждый из них.

Задача №3. Нестандартная задача.

Для измерения высоты холма отошли от него по прямой линии и отметили на этой прямой точку D, из которой холм виден под углом в 30º, затем – точку С, из которой холм виден под углом в 15˚.

Какое расстояние нужно измерить на местности, чтобы найти высоту холма?

Можно ли решить эту задачу, не применяя теорему синусов и теорему косинусов?

Задача №4.

На расстоянии 1500 м от подножия горы находится лыжная база.

От подножия горы до вершины 2 км. Какой длины должен быть подъемник, чтобы лыжники могли подниматься на вершину горы

Прямо от лыжной базы, если угол наклона горы 110˚.

V. Защита работ(от каждой группы выступает ученик)

Слово учителя.

Мне очень бы хотелось, чтобы геометрия помогла вам научиться видеть красоту этого удивительного мира.

«… В одно мгновенье видеть вечность,

Огромный мир – в зерне песка,

В единой горсти – бесконечность

И небо – в чашечке цветка»

Поэт Вильям Блейк.

VI. Подведение итогов.

Рефлексия(презентация)

Домашнее задание: задача № 4.