
Огромная заслуга тестов состоит в том,
что они позволяют обычный ответ учителя
«так мне кажется» заменить словами
«я это знаю» или «я это не знаю»
П.П. Блонский
Проблемы формирования функциональной грамотности личности при переходе на 12-юю систему обучения является основной задачей образования. На это нацелена государственная программа развития образования РК на 2011-2020 годы. Целью этой программы является: воспитание конкурентноспособной личности путем обеспечения доступности качественного образования, обеспечение учащимся равного доступа к образовательным ресурсам и технологиям.
Задача усовершенствования преподавания математики включает использование различных методов обучения и контроля. Один из таких методов – тестовый контроль знаний учащихся, который в последнее время всё больше входит в жизнь современной школы. Использование тестов на уроке вносит разнообразие в учебную работу, повышает интерес к предмету, способствуя тем самым лучшему усвоению знаний. Сегодня школы поставлены перед необходимостью подготовить ученика к проверке знаний в форме ЕНТ, и поэтому применение тестов на уроках актуально как одна из форм и методов подготовки к итоговой аттестации.
Данное учебно-методическое пособие представляет собой сборник тестов, составленных к разделу геометрии - планиметрия.
Не секрет, что изучение геометрии в школе вызывает большие трудности у школьников. Так как алгоритмизировать процесс решения геометрических задач сложнее, чем решение задач по алгебре, поэтому многие школьники не в состоянии увидеть общие подходы и идеи решения геометрических задач. Использование сборника тестов, в первую очередь, способствует выявлению представлений учеников об основных идеях решения геометрических задач. Одним из важнейших умений, приобретаемых в курсе планиметрии, является умение понимать текст задачи, выделять в тексте задачи условие и заключение, читать и делать чертежи, сопровождающие задачи, а при чтении чертежа выделять конфигурацию, необходимую на данном этапе решения задачи. Не все темы планиметрии равнозначны. Анализ «Требований к математической подготовке учащихся» и «Тематического планирования» позволил выделить основные ключевые темы. По этим темам создан сборник.
Материал, содержащийся в данном сборнике, позволит помочь учащимся научиться уверенно, выполнять задания как стандартные, так и нестандартные.Тесты предназначены как для учащихся, проявляющих интерес к математике, так и для желающих проверить уровень своих знаний по указанной теме.
Все задания отвечают требованиям школьной программы. Данный сборник тестов может быть использован при проведении самостоятельных и контрольных работ с целью проверки уровня усвоения знаний учащимися по данным темам, при повторении материала в конце учебного года, а так же при подготовке учащихся к ВОУД и ЕНТ по математике. Это пособие может быть использовано учителями на уроках математики в классе, а так же учениками при самостоятельной подготовке дома.
Тесты разделены по уровню сложности, что даёт возможность дифференцированного подхода к каждому ученику. Также для более сильных учеников возможно использование для устного счёта. Задания тестов позволяют предложить ученику выполнить большой объём работы за небольшое время. Таким образом, оттачиваются не только вычислительные навыки, формируется «числовая зоркость», но и тренируется внимание при работе с тестами, что важно для сдачи ЕНТ, развивается оперативная память ребёнка. В результате работы с тестами ученик приучается быстро и правильно считать и думать, овладевает различными приёмами самопроверки, значительно лучше ориентируется в числовых множествах. Задания теста можно предлагать как для индивидуальной, так и для коллективной работы в классе.
Содержание
Введение……………………………………………………………………………
Треугольники ……………………………………………………………………
Четырехугольники…………………………………………………………………Окружность, круг ………………………………………………………………
Окружности, вписанные в треугольники и четырехугольники, описанные около треугольника и четырехугольника………………………………………..
Векторы……………………………………………………………………………
Декартовы координаты……………………………………………………………
тема: Треугольники
Уровень «А»
1.В равнобедренном прямоугольном треугольнике гипотенуза равна  см. Вычислите сумму катетов треугольника.
см. Вычислите сумму катетов треугольника.
A) 26 см
B) 28 см
C) 30 см
D) 24 см
E) 22 см
2. Найдите углы равнобедренного треугольника, если его высота вдвое меньше биссектрисы угла при основании.
А) 30° ,30° ,120°
В) 45° ,45° ,90°
С) 36° ,36° ,108°
D) 50° ,50 °,80°
Е) 40°,40 °,100°
3.В равнобедренном треугольнике боковая сторона 10 см, основание 16 см. Определите высоту, опущенную на боковую сторону.
A) 9,2 см
B) 9,4 см
C) 10,2 см
D) 9,6 см
E) 9,8 см
4.Катеты прямоугольного треугольника равны. Определите их длину, если площадь треугольника 18 см
A) 9 см
B) 6 см
C) 3 см
см
D) 8 см
E) 3 см
см
5.Один катет треугольника на 7 см больше другого, а площадь равна 30 см . Определите больший катет прямоугольного треугольника.
. Определите больший катет прямоугольного треугольника.
A) 13см
B) 14см
C) 10см
D) 15см
E) 12см
6.Площадь прямоугольного треугольника 6 см , а гипотенуза 5 см. Найдите разность катетов.
, а гипотенуза 5 см. Найдите разность катетов.
A) 1см
B) 2см
C) 4см
D) 3см
E) 1,5см
7.Найдите отношение катетов прямоугольного треугольника, если гипотенуза равна 26 см и катет 10 см.
A) 13 : 4
B) 13 : 12
C) 12 : 5
D) 10 : 3
E) 13 : 5
8.В прямоугольном треугольнике один катет на 6 см больше другого. Найдите меньший катет, если гипотенуза равна 30 см.
A) 12см
B) 16 см
C) 24 см
D) 18 см
E) 20 см
9.В прямоугольном треугольнике катет и гипотенуза равны 30 см, 50 см. Вычислите высоту, проведённую из прямого угла.
A) 24 см
B) 27 см
C) 16 см
D) 18 см
E) 20 см
10.Катеты прямоугольного треугольника равны 21 см и 28 см. Определите синус меньшего угла.
A) 0,4
B) 0,6
C) 0,7
D) 0,8
E) 0,9
11.В прямоугольном треугольнике сумма катетов равна 56 см, а гипотенуза 40 см. Найдите меньший катет.
A) 22 см
B) 26 см
C) 18 см
D) 24 см
E) 25 см
12.Катеты прямоугольного треугольника относятся как 3:4, а гипотенуза равна 55 см. Найдите периметр треугольника.
A) 134 см
B) 146 см
C) 132 см
D) 122 см
E) 116 см
13.Катет прямоугольного треугольника равен 24см, а гипотенуза 40см. Определите высоту этого треугольника.
A) 18,4 см
B) 18,3 см
C) 18,8 см
D) 19,2 см
E) 17,8см
14. Гипотенуза прямоугольного треугольника равна 18 см. Чему равна медиана, проведенная к гипотенузе?
A) 8 см
B) 11 см
C) 12 см
D) 10 см
E) 9 см
15. Найти длину высоты прямоугольного треугольника, опущенной из прямого угла, если она делит гипотенузу на отрезки, равные 3 и 27 см.
A) 7 см
B) 5 см
C) 2 см
D) 4 см
E) 9 см
Уровень «В»
1.Найти косинус меньшего угла треугольника со сторонами 13 см, 14 см и 15 см.
A) 0,8
B) 0,7
C) 0,5
D) 0,4
E) 0,6
2.Гипотенуза прямоугольного треугольника равна 20 см. Найдите разность катетов, если они пропорциональны числам 3:4.
A) 5см
B) 4см
C) 6см
D) 2см
E) 3 см
3.В равнобедренном треугольнике боковая сторона равна 20 см, а основание относится к высоте как 8:3. Найдите радиус вписанной окружности.
A) 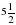 см
см
B)  см
см
C)  см
см
D) 5 см
E) 
4.Чему равен больший угол в треугольнике со сторонами 5 см, 5 см и 10 см?
см, 5 см и 10 см?
A) 75°
B) 45°
C) 90°
D) 30°
E) 60°
5.Определите косинус большего угла треугольника, если его стороны: 7 см, 8 см и 9 см.
A) 
B) 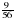
C) 
D) 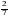
E) 
6.Площадь прямоугольного треугольника 60 см , а сумма катетов 23 см. Найдите гипотенузу треугольника.
, а сумма катетов 23 см. Найдите гипотенузу треугольника.
A) 19см
B) 16см
C) 18см
D) 17см
E) 15см
7.Площадь прямоугольного треугольника 96 см  , а его высота 9,6 см. Найдите сумму катетов этого треугольника.
, а его высота 9,6 см. Найдите сумму катетов этого треугольника.
A) 27см
B) 28см
C) 30см
D) 26см
E) 32см
8.Катет прямоугольного треугольника равен 21 см, а гипотенуза 35 см. Определите высоту этого треугольника.
A) 17,4 см
B) 17,3 см
C) 16,8 см
D) 17,2 см
E) 16,6см
9.В прямоугольном треугольнике катеты равны 21см и 28 см. Найдите косинус большего острого угла.
A) 0,3
В) 0,7
С) 0,5
D) 0,4
Е) 0,6
10.Площадь прямоугольного треугольника 180 см , а катет 40 см. Укажите разность гипотенузы и другого катета.
, а катет 40 см. Укажите разность гипотенузы и другого катета.
A) 32 см
B)28 см
C) 31 см
D) 34 см
E) 29 см
11.Гипотенуза прямоугольного треугольника равна 26 см, а площадь 120 см . Найдите меньший катет.
. Найдите меньший катет.
A) 12 см
B) 14 см
C) 10 см
D) 13 см
E) 11 см
12.Площадь прямоугольного треугольника 24 см , а его высота 4,8 см. Найдите сумму катетов этого треугольника.
, а его высота 4,8 см. Найдите сумму катетов этого треугольника.
A) 18см
B) 14см
C) 15см
D) 16см
E) 22см
13.Отрезок ОА длиной 24 см перпендикулярен плоскости квадрата АВСD со стороной 5 см. Определите расстояние ОС.
см. Определите расстояние ОС.
A) 28 см
B) 26 см
см
C) 24 см
см
D) 26 см
E) 22 см
14.В прямоугольном треугольнике катеты равны 3 и 4 соответственно. Найдите длины отрезков, на которые делит гипотенузу биссектриса прямого угла
A) 
B) 2; 3
C) 
D) 1; 4
E) 
15. Найти боковую сторону равнобедренного треугольника АВС, если угол при основании равен 30о и высота, опущенная на боковую сторону, равна 3
A) 
B) 
C) 
D) 
E) 
Уровень «С»
1.В треугольнике стороны равны: 18см, 26см, 32см. На какие отрезки разобьёт сторону биссектриса, проведённая из меньшего угла? Укажите набольший из них.
A) 11 см
см
B)  см
см
C)  см
см
D)  см
см
E)  см
см
2.Из середины меньшей стороны АВ к плоскости прямоугольника АВСD проведён перпендикуляр ОМ длиной 6 см. Найдите длину МС, если стороны прямоугольника 16 см и 24 см.
A) 24 см
B) 28 см
C) 27 см
D) 32 см
E) 26 см
3.Определите косинус наибольшего угла треугольника, если стороны равны 7 см, 11 см и 14 см
A) 
B) 
C) 
D) –
E) 
4. Синус угла между сторонами треугольника равными 10 см и 16 см равен  . Найдите сумму синусов двух других углов.
. Найдите сумму синусов двух других углов.
A) 
B) 
C) 
D) 
E) 
5.В треугольнике две стороны равны 5 см и 6 см, а синус угла между ними 0,8. Найдите медиану, проведённую к большей стороне.
A) 5,2 см
B) 4,8 см
C) 4 см
D) 4,4 см
E) 4,6 см
6.Стороны угла АСВ, равного 60о, касаются двух окружностей с центрами О1 и О2, касающихся одна другой. (О2 – центр меньшей окружности). СО1 = 12 см. Найдите радиус окружности с центром О2
A) 2 см
B)  см
см
C)  см
см
D) 3 см
E)  см
см
7. В треугольнике АВС угол А равен 450, угол В равен 150, АВ= . Найдите ВС.
. Найдите ВС.
A) 
B) 
C) 
D) 
E) 
8. Найти углы равнобедренного треугольника, если известно, что найдется прямая, проходящая через вершину угла при основании, делящая исходный треугольник на два равнобедренных.
А) (36° ,72° ,72° ) и (80° ,80° ,20°)
Е) (45°, 45°, 90°) и (60°,60°,60°).
В) (75° ,75° ,30° ) и (50° ,50 °,80 °)
С) (36° ,36° ,108° ) и (25 5/7° ,77 1/7° ,77 1/7° )
D) (36 °,72 ° ,72° ) и (25 5/7° ,77 1/7° ,77 1/7° )
тема: Четырехугольники
Уровень «А»
1.В равнобокой трапеции высота, проведенная из вершины тупого угла, делит большее основание на отрезки 6 см и 30 см. Найдите основания трапеции
A) 26 см и 34 см
B) 12 см и 24 см
C) 24 см и 36 см
D) 41 см и 20 см
E) 22 см и 32 см
2.Найдите углы параллелограмма, если один из них больше другого на 50о
A) 65о и 115о
B) 125о и 55о
C) 75о и 105о
D) 50о и 130о
E) 60о и 120о
3.Прямоугольник с периметром 88 см разбили параллельными линиями на 3 равные части через сторону равную 12 см. Назовите периметр среднего из прямоугольников.
A) 72см
B) 80 см
C) 68 см
D) 70 см
E) 74 см
4.Диагональ прямоугольника, равная 16 , наклонена к стороне под углом 45°. Определите периметр прямоугольника.
, наклонена к стороне под углом 45°. Определите периметр прямоугольника.
A) 72 см
B) 58 см
C) 60 см
D) 48 см
E) 64 см
5.Одна сторона прямоугольника составляет 35% другой стороны. Определите большую сторону прямоугольника, если периметр равен 54 см.
A) 19см
B) 17см
C) 16см
D) 18см
E) 20 см
6.Полупериметр параллелограмма равен 47 см. Найдите меньшую сторону, если она на 13 см меньше другой.
A)18 см
B) 17 см
C) 16 см
D) 15 см
E) 14 см
7.Углы параллелограмма пропорциональны числам 7:5. Чему равна разность двух углов при стороне параллелограмма.
A) 32°
B) 36°
C) 30°
D) 20°
E) 24°
8.Диагональ параллелограмма образует с двумя его сторонами углы 23° и 38°. Назовите больший угол параллелограмма.
A) 139°
B) 141°
C) 119°
D 129°
E) 137°
9.На сторону параллелограмма равную 18 см проведена высота длиной 15 см. Определите другую сторону, если высота, падающая на неё, равна 9 см.
A) 36 см
B) 30 см
C) 27 см
D) 32 см
E) 25 см
10.Найдите больший угол параллелограмма, если сумма двух углов равна 154°.
A) 103°
B) 113°
C) 144°
D) 132°
E) 116°
11.Диагонали ромба равны 24 см и 70 см. Определите сторону ромба.
A) 43 см
B) 37 см
C) 46 см
D) 51 см
E) 36 см
12.Два угла ромба относятся как 1:2. Определите периметр ромба, если его меньшая диагональ равна 12 см.
A) 44 см
B) 60 см
C) 48 см
D) 54 см
E) 64 см
13.Два угла трапеции равны 123° и 71° . Определите меньший угол.
A) 59°
B) 67°
C) 69°
D) 54°
E) 57°
14.Средняя линия трапеции равна 18 см, а верхнее основание на 8 см меньше нижнего. Определите меньшее основание.
A) 12 см
B) 15 см
C) 14 см
D) 11 см
E) 13 см
15.Боковые стороны трапеции равны 17 см и 19 см, а периметр 66 см. Определите среднюю линию трапеции.
A) 16 см
B) 15 см
C) 14 см
D) 17 см
E) 18 см
Уровень «В»
1.Найти площадь четырехугольника ABCD, если АВ = 5, ВС = 13, CD = 9,AD = 15 АС = 12
A) 98
B) 104
C) 108
D) 84
E) 88
2.Дан квадрат со стороной 1 м, а диагональ его равна стороне другого квадрата. Найдите диагональ последнего.
A) 14 м
B) 4 м
C) 0,5 м
D) 1 м
E) 2 м
3.Одна диагональ параллелограмма 20 см, а стороны 10 см и 14 см. Определите другую диагональ.
A)10 см
см
B)6 см
см
C)10 см
см
D)12 см
см
E) 8 см
см
4.Найдите тупой угол ромба, если диагональ, проведенная из острого угла, образует с его стороной угол в 40о
A) 160о
B) 120о
C) 140о
D) 280о
E) 100о
5.Угол между диагональю прямоугольника и стороной равной 10 см, равен 60°. Найдите периметр прямоугольника.
A) 50 см
см
B) 5(4 +3) см
+3) см
C) 40( +2) см
+2) см
D) 40 см
E) 20( +1) см
+1) см
6.Биссектрисы, проведенные из двух противоположных углов прямоугольника, отсекли от него ромб со стороной  см. Определите периметр прямоугольника.
см. Определите периметр прямоугольника.
A) 4+4 см
см
B) 6+ см
см
C) 8+ см
см
D) 4+2 см
см
E) 30 см
7.Стороны параллелограмма, заключающие угол 45°, равны 5 см и 8 см.
см.
Определите меньшую диагональ параллелограмма.
A) 
B) 
C) 
D) 
E) 
8.Чему равны диагонали ромба, если они пропорциональны числам 3:4 , а сторона ромба равна 35см?
A) 62 см и 28 см
B) 32 см и 48 см
C) 44 см и 38 см
D) 56 см и 42 см
E) 58 см и 34 см
9.Определите острый угол параллелограмма, если высота равна 21 см, а сторона, на которую не падает эта высота, равна 14 см.
см.
A) 55°
B) 75°
C) 45°
D) 60°
E) 30°
10.Одна диагональ параллелограмма 10 см, а стороны 5 см и 7 см. Определите другую диагональ.
A) 10 см
см
B) 4 см
см
C) 10 см
см
D) 12 см
см
E) 6 см
см
11.Периметр ромба равен 40 см, а радиус вписанной окружности равен 4 см. Определите синус острого угла.
A) 0,5
B) 0,65
C) 0,75
D) 0,8
E) 0,6
12.В равнобокой трапеции диагональ равна 26 см, высота равна 10 см, а верхнее основание равно 14 см. Под каким углом наклонена боковая сторона?
A) 60°
B) 45°
C) 30°
D) 15°
E) 75°
13.Основания трапеции относятся как 4:7. Найдите верхнее основание, если средняя линия равна 28,6 см.
A) 21,2 см
B) 19,6 см
C) 21,6см
D) 22,4 см
E) 20,8 см
14.Высота, проведённая из вершины тупого угла равнобедренной трапеции, делит большее основание на отрезки 7 см и 19 см. Вычислите среднюю линию трапеции.
A) 19 см
B) 21 см
C) 18 см
D) 17 см
E) 16 см
15. В параллелограмме с высотой √2см, один угол в три раза больше другого угла, тогда
А) одна из сторон равна 2см
В) одна из сторон короче на 2см, а другая длиннее на 2см
С) обе стороны короче на 2см
D) обе стороны длиннее на 2см
Е) стороны короче высоты.
Уровень «С»
1.Одна диагональ параллелограмма 20 см, а стороны 10 см и 14 см. Определите другую диагональ.
A) 10 см
см
B) 6 см
см
C) 10 см
см
D) 12 см
см
E) 8 см
см
2.Два угла ромба относятся как 2:1. Определите периметр ромба, если егоменьшая диагональ равна 14 см.
A) 64 см
B) 60 см
C) 58 см
D) 56 см
E) 54 см
3.Одна из диагоналей ромба равна его стороне. Определите периметр ромба, если другая диагональ равна 18 см.
см.
A) 74 см
B) 88 см
C) 72 см
D) 78 см
E) 86 см
4.Основания трапеции 12 см и 22 см. Найдите длину отрезка проведённого через точку пересечения диагоналей, параллельно основаниям.
A)  см
см
B)  см
см
C)  см
см
D)  см
см
E) 
5.Боковые стороны трапеции равны 17 см и 23 см, а основания 12 см и 28 см. Определите высоту трапеции.
A)  см
см
B)  см
см
C)  см
см
D)  см
см
E)  см
см
6.Основания трапеции равны 12 см и 16 см. Боковые стороны соединены отрезком, параллельным основаниям и делящим трапецию на две равновеликих части. Найдите длину этого отрезка.
A) 12,5см
B) 13см
C) 10 см
см
D) 12 см
см
E) 14 см
7.Основания равнобокой трапеции равны 10 см и 24 см. Определите длину отрезка, проведённого параллельно основаниям и делящего трапецию на две равновеликих трапеции.
A) 10 см
см
B) 15 см
см
C) 14 см
см
D) 12 см
см
E) 13 см
см
8.Стороны параллелограмма, заключающие угол в 60о, равны 2 см и 3 см. Найдите диагональ, лежащую против этого угла.
А) 4 см.
В) 3,7 см.
С)  см
см
Д)  см
см
Е) 2 см
9. Найти среднюю линию равнобедренной трапеции с высотой h., если боковая сторона видна из центра описанной окружности под углом 120°.
А) √3h
3
В) 0,6h
C) √2h
3
D) 0,8h
E) 2h
3
тема : Окружность, круг
Уровень «А»
1.Найдите диаметр окружности, если известно, что он больше радиуса этой окружности на 10 см.
А) 20
В) 25
С) 35
Д) 10
Е) 30
2.Вычислите длину окружности, если радиус равен 10 м
A) 10 м
м
B) 40 м
м
C) 20 м
м
D) 30 м
м
E) 35 м
м
3.К окружности проведена касательная. Через точку касания проведена хорда, отрезающая от окружности дугу в 96˚. Чему равен угол между хордой и касательной?
A) 48˚
B) 44˚
C) 96˚
D) 84˚
E) 42˚
4.Найдите длину дуги окружности радиуса 20 см, если центральный угол, соответствующий этой дуге, равен 2,5 радиан.
A) 30 см
B) 40 см
C) 45см
D) 50 см
E) 35 см
5.Определите градусную меру центрального угла, если площадь круга равна 225 π см , а площадь сектора равна 75π см
, а площадь сектора равна 75π см .
.
A)160˚
B)150˚
C) 140˚
D)170˚
E)120˚
6.Площадь круга равна 12 . Найдите его диаметр.
A)  см
см
B)  см
см
C)  см
см
D)  см
см
E)  см
см
7.Из точки вне окружности, радиуса 9 см, проведена касательная, с расстоянием до точки касания 40 см. Определите расстояние от этой точки до центра окружности.
A) 46 см
B) 45 см
C) 41 см
D) 48 см
E) 47 см
8.Вписанный угол опирается на дугу 140˚. Определите величину другого вписанного угла, опирающегося на оставшуюся часть окружности.
A) 120˚
B) 135˚
C) 115˚
D) 110˚
E) 130˚
9.В окружности проведены пересекающиеся хорды АК и ВС.  ВАК = 47˚, а
ВАК = 47˚, а  ВКС = 112˚. Определите
ВКС = 112˚. Определите  СВК.
СВК.
A) 28˚
B) 42˚
C) 46˚
D) 33˚
E) 21˚
10.Длина дуги с градусной мерой 210˚ равна 14 π см. Найдите площадь целого круга.
A) 196 π см
B) 169 π см
C) 121 π см
D) 144 π см
E) 225 π см
11. Диаметр и хорда окружности составляют угол 30°. Зная, что радиус окружности 6см, найдите длину диаметра и хорды.
А) 3 и 2
В) 12 и 6
С) 3 и 3
D) 2 и 3
Е) 2 и 
12. В окружности с центром в точке О и радиусом 10см, проведена хорда МР=16см, тогда расстояние от центра окружности до хорды равно
А) 
В) 12
С) 6
D) 
Е) 2
13. В окружности длиной 24π м проведена хорда, равная 12м. Найдите градусную меру меньшей дуги, стягиваемой хордой.
А) 45°
В) 30°
С) 60°
D) 90°
Е) 120°
14. Какой наибольший центральный угол может иметь правильный многоугольник?
A) 60°
B) 90°
С) 135°
D) 120°
E) 150°
15. Отрезки касательных АВ и АС, проведенных из точки А к окружности с центром О, образуют угол, равный 60˚, ОВ = 15 см. Чему равен отрезок ОА?
A) 40 см
B) 7,5 см
С)45 см
D) 30 см
E) 60 см
Уровень «В»
1. Площади двух кругов равны 625 π см и 225π см
и 225π см . Найдите отношение их диаметров.
. Найдите отношение их диаметров.
A) 5: 2
B) 3: 2
C) 5:3
D) 5: 4
E) 4: 3
2.Периметр правильного шестиугольника равен 24 см. Найдите его площадь.
A) 20 см
см
B) 32 см
см
C) 36 см
см
D) 24 см
см
E) 28 см
см
3.Из дуги окружности радиусом 10 см и центральным углом 270˚ свернули окружность, ограничивающую круг. Определите площадь нового круга.
A) 54,76 π см
B) 42,25 π см
C) 60,84 π см
D) 56,25 π см
E) 72,25 π см
4.Найдите площадь сектора радиуса 18 см, если вписанный угол, опирающийся на дугу сектора, равен 40˚.
A) 40 π см
B) 64 π см
C) 72 π см
D) 48 π см
E) 36 π см
5.Каким должен быть радиус окружности, если её длина в 4 раза больше сумм длин окружностей с радиусами 13 см и 29 см?
A) 84 см
B) 72 см
C) 168 см
D) 332 см
E) 42 см
6.Стороны двух, правильных шестиугольников отличаются в 3 раза. Определите площадь меньшего из них, если сторона большего равна 24 см.
A) 84 см
см
B) 96 см
см
C) 76 см
см
D) 102 см
см
E) 98 см
см
7.Oпределите длину хорды, стягивающей дугу в 120˚, если радиус окружности равен 6 см.
см.
A) 84 см
B) 72 см
C) 166 см
D) 18см
E) 42 см
8.Если длина окружности увеличится в 19 раз, то во сколько раз увеличится площадь ограниченного ею круга?
A) В 19 раз
раз
B) В 361 раз
C) В 324 раз
D) В 360 раз
E) В 19 раз
9.Во сколько раз увеличится радиус, если площадь круга увеличится в два раза?
A) В 3 раза
B) В  раз
раз
C) В раз
раз
D) В 2 раза
E) В 0,5 раза
10. Найти площадь сектора радиуса 3см, если соответствующий этому сектору центральный угол равен 30°.
А) π/2
В) 7π/2
С) 2,5π
D) 3π/4
Е) 1,5π
11. В окружности длиной 36π см проведена хорда, стягивающая дугу в 60° . Найдите длину хорды.
А) 12
В) 6
С) 18
D) 18
E) 6
12. Из точки А, удаленной от окружности на 8м, проведена касательная к окружности. Найдите расстояние от точки касания до прямой, проходящей через точку А и центр окружности, если радиус равен 5м.
А) 
В) 3
С) 5
D) 8
Е) 
13. Из одной точки окружности проведены две хорды длиной 9см и 17см. Найти площадь круга, если расстояние между серединами хорд равно 5см.
А) 25π
В) 7225π
64
С) 100, 25π
D) 100π
Е) 36π
14. Хорды АВ и CD пересекаются в точке Х. Найдите длину CD, если АX =6 см, ВX = 5 см, а длина СX на 1 см меньше длины DХ.
А) 6 см
В) 14 см
С) 11см
Д ) 12 см
Е) 8 см
15. Прямая АВ касается окружности с центром О радиуса 6 см. Известно, что АВ = 16 см, АО = ОВ. Чему равна длина АО?
А) 8 см
В) 10 см
С) 6 см
Д) 9 см
Е) 16 см
Уровень «С»
1.Определите градусную меру центрального угла, если площадь круга равна S, а площадь сектора равна G.
A) 
B) 
C) 
D) 
E) 
2.Длина дуги, ограничивающей сектор площадью 189 π см , равна 21π см. Определите градусную меру центрального угла.
, равна 21π см. Определите градусную меру центрального угла.
A) 170°
B) 240°
C) 150°
D) 230°
E) 210°
3.Сектор с радиусом 6 см и углом 300˚ равновелик с другим сектором с центральным углом в 200˚. Определите радиус второго сектора.
A) 5 см
см
B) 4 см
см
C) 3 см
см
D) 6 см
см
E) 4 см
см
4.Расстояние между центрами двух окружностей равно 35 см, а их радиусы равны 21 см и 28 см. Определите расстояние между точками пересечения окружностей.
A) 42,8 см
B) 33,6 см
C) 37,9 см
D) 28,4 см
E) 31,2 см
5.Из алюминиевой трубки изготовили пять разных обручей для гимнастики. Диаметр каждого следующего обруча был на 0,1 м больше предыдущего. Определите диаметр меньшего обруча, если затрачено 5 π м трубки.
A) 0,95 м
B) 0,7 м
C) 1 м
D) 0,9 м
E) 0,8 м
6. Угол АВС—вписанный в окружность, О – центр окружности. Хорда АВ=m, а угол АСВ=α/2. Найдите радиус окружности.
А) m
2 sin2α
B) m
2 sin(α/2)
C) m
2 sinα
D) m
sin2α
E) 2 m
sin2α.
7. Три окружности попарно касаются друг друга. Отрезки, соединяющие их центры, образуют прямоугольный треугольник. Найдите радиус меньшей окружности, если радиусы двух других равны 6 и 4.
А) 5
В) 4
С) 1
D) 3
Е) 2
тема: Окружности, вписанные в треугольники и четырехугольники, описанные около треугольника и четырехугольника
Уровень «А»
1.Длина окружности, описанной около правильного треугольника равна 20 π см. Найдите площадь такого круга.
A) 112 π см
B) 108 π см
C) 96 π см
D) 100 π см
E) 116 π см
2.Найдите длину окружности, описанной около прямоугольного треугольника с катетами 4 дм и 3 дм
A) 2 дм
дм
B) 5 дм
дм
C) 20 дм
дм
D)  дм
дм
E) 10 дм
дм
3.Один из катетов прямоугольного треугольника равен 10 дм, а радиус описанной около этого треугольника окружности равен 13 дм. Найдите площадь этого треугольника
A) 120 дм2
B) 240 дм2
C) 80 дм2
D) 60 дм2
E) 39 дм2
4.В четырехугольник ABCD вписана окружность. Известно, что АВ = 15 см, ВС = 21 см, CD = 18 см. Какое из следующих утверждений верно?
A) Длина стороны AD равна 12 см
B) Сторона AD короче CD, но длиннее АВ
C) Сторона AD длиннее CD
D) Сторона AD короче ВС, но длиннее CD
E) Длина стороны AD равна 14 см
5.Радиус вписанный в равносторонний треугольник окружности равен 3см.Найдите высоту треугольника
A) 9 см
B) 8 см
C) 6 см
D) 7 см
E)  см
см
6.Дан треугольник АВС.  , ВС = 6. Найти радиус описанной окружности.
, ВС = 6. Найти радиус описанной окружности.
A) 10
B) 12
C) 6
D) 18
E) 3
7.В окружность вписан прямоугольник со сторонами 12 см и 5 см. Найдите длину окружности
A) 22 см
см
B) 17 см
см
C) 52 см
см
D) 13 см
см
E) 26 см
см
Уровень «В»
1.Площадь круга, описанного около шестиугольника равна 36 π см .Найдите площадь правильного шестиугольника.
.Найдите площадь правильного шестиугольника.
A) 66 см
см
B) 48 см
см
C) 56 см
см
D) 72 см
см
E) 54 см
см
2.В правильный шестиугольник со стороной 12 см вписана окружность, площадь которой необходимо найти.
A) 118 π см
B) 144 π см
C) 98 π см
D) 108 π см
E) 112 π см
3.Площадь правильного шестиугольника равна 24 см
см . Найдите площадь круга, описанного около шестиугольника.
. Найдите площадь круга, описанного около шестиугольника.
A) 20 π см
B) 18 π см
C) 36 π см
D) 24 π см
E) 16 π см
4. Стороны прямоугольника пропорциональны числам 2 и 3, а его площадь 54. Определите площадь круга, описанного около прямоугольника.
A) 
B) 
C) 
D) 
E) 
5.В прямоугольный треугольник вписана окружность. Точка касания делит гипотенузу на отрезки, равные 2 и 3. Найти радиус этой окружности.
A) 2
B) 5
C) 7
D) 1
E) 3
Уровень «С»
1.В правильный шестиугольник вписан правильный треугольник. Найдите отношение их площадей.
A) 3:2
B) 3:1
C) 2:1
D) 4:3
E) 4:1
2.Найдите отношение площади круга, вписанного в шестиугольник к площади круга описанного около него.
A) 0,8
B) 0,85
C) 0,9
D) 0,75
E) 0,95
3.Вершины квадрата являются центрами взаимно касающихся окружностей с радиусами по 8 см. Найдите радиус окружности, касающейся всех четырех окружностей внутри квадрата.
A) 8(1- ) см
) см
B) 8 см
см
C) 8( ) см
) см
D) 8 см
см
E) 8( ) см
) см
тема: Векторы
Уровень «А»
1.Определите длину вектора  , если известны координаты точек А(-5; 4) и В(3; -2).
, если известны координаты точек А(-5; 4) и В(3; -2).
A) 2
B) 2
C) 10
D) 2
E) 12
2.Определите длину вектора  , если известны координаты точек А{-6; 7) и В(2; 13).
, если известны координаты точек А{-6; 7) и В(2; 13).
A) 10
B) 2
C) 2
D) 2
E) 12
3.Вычислите длину вектора  , если даны координаты векторов
, если даны координаты векторов  и
и  .
.
A) 5 см
см
B) 7 см
см
C) 6 см
см
D) 8 см
см
E) 9 см
см
4.Вычислите координаты вектора  , если
, если  и
и 
A) 
B) 
C) 
D) 
E) 
5.Определите длину вектора  , если
, если  и
и 
A) 
B) 
C) 
D) 
E) 
6.Даны точки А(-3;7), В(-1;-1), С(5;3). Определите координаты точки К, если  A) (3;11)
A) (3;11)
B) (9;9)
C) (-7;5)
D) (7;-5)
E) (7;5)
7.Чему равна сумма векторов  +
+ +
+ +
+ +
+ +
+ +
+ ?
?
A) 
B) 
C) 
D) 
E) 
8.Длины векторов  и
и  равны 16 и 9, а угол между ними 60°. Найти их скалярное произведение.
равны 16 и 9, а угол между ними 60°. Найти их скалярное произведение.
A) 84
B) 72
C) 144
D) 96
E) 86
9.Вектора  и
и  параллельны. Найдите значение числа р, если
параллельны. Найдите значение числа р, если 
 и
и 
 .
.
A) -14
B) 21
C) 14
D) -35
E) -21
10.Найти скалярное произведение  , если
, если  =6
=6 ,
,  =8. а угол между ними равен 30°
=8. а угол между ними равен 30°
A) 72
B) 74
C) 76
D) 48
E) 24
11.Дан равносторонний треугольник АВС, сторона которого равна 6 см. Вычислите скалярное произведение  .
.
A) 24
B) 36
C) -18
D) 18
E) -36
12.Дан ромб АВСD со стороной 12 см. Определите 
A) 72
B) -144
C) 144
D) -72
E) -72
13. Найдите периметр треугольника МРК, если М(6;-8), Р(13;-1) и К( -2; 7).
A ) 17+6
B) 18+4
C) 34+7
D) 51+
E) 34+5
Уровень «В»
1.Даны три точки А(-4;-2), В(1;2), С(2;-2). Определите координаты точки М(х;у), чтобы выполнялось равенство: 
A) (3;6)
B) (-3;-6)
C) (-7;2)
D) (7;-2)
E) (7;2)
2.Точка М(1;-3) является серединой вектора  . Определите координаты точки А, если точка В(-3;2).
. Определите координаты точки А, если точка В(-3;2).
A) (4;5)
B) (-2;-1)
C) (5 ; -8)
D) (7;-5)
E) (-7;5)
3.Даны два вектора:  и
и  . Найдите значение числа m, если вектора коллинеарны.
. Найдите значение числа m, если вектора коллинеарны.
A) 10
B) 7
C) 9
D) 12
E) 8
4.Вектора  и
и  коллинеарны и сонаправлены. Определите координаты точки D, если
коллинеарны и сонаправлены. Определите координаты точки D, если  = 3
= 3 , а
, а  и С(4;-1).
и С(4;-1).
A) (12;-3)
B) (-9;12)
C) (5;-11)
D) (9;-12)
E) (-5;11)
5.Найдите координаты точки М, одной из вершин ромба MNPK, если N(6;-3), P(1;2), K(2;9).
A) ( 5; 5)
B) ( 4;7)
C) (7;4)
D) (6; 5)
E) ( 7;5)
6.Найдите координаты точки D, одной из вершин трапеции АВСD, если А(0;8), В(6;7), С(8;1) и верхнее основание ВС в 2 раза короче нижнего АD.
A) ( 4; 5)
B) ( 3;-2)
C) (5;-1)
D) (4; -4)
E) ( 4;-6)
7.Вектора  и
и  перпендикулярны. Найдите значение числа р, если
перпендикулярны. Найдите значение числа р, если 
 ,
, 
 .
.
A) 2
B) 1
C) -2
D) 3
E) -1
8.Определите косинус угла между векторами 
 и
и 
 .
.
A) 
B) 
C) 
D) 
E) 
9.Определите синус угла между векторами 
 и
и 
 .
.
A) -1
B) 
C) 0
D) 1
E) 
10.Определите косинус угла между векторами, если их скалярное произведение равно 3, а длины векторов 2 см и 3 см.
см.
A) 
B) 
C) 
D) 
E) 
11.Найдите значение числа р, если 


 и их скалярное произведение равно – 16.
и их скалярное произведение равно – 16.
A) 4
B) 8
C) 4
D) 4
E) – 4
12. Найдите угол между векторами 
 ,
, 
 .
.
A) 180°
B) 45°
C) 30°
D) 60°
E) 90°
13.В треугольнике с вершинами в точках M (2; -3), N (-4; 6) и K (5; -1), определите косинус угла M.
A) 0,5
B) 0
C) 0,4
D) 0,6
E) 0,3
14. Вычислите длину вектора  =
= , если даны координаты векторов
, если даны координаты векторов 
A) 2
B) 
C) 1
D) 
E) 3
Уровень «С»
1.Определите косинус меньшего угла треугольника АВС, если известны координаты всех точек: А(–5;7), В( 3;–1), С(–1;–9).
A) 
B) 
C) 
D) 
E) 
2.Определите координаты центра тяжести треугольника с вершинами в точках M(-3; 5), P(13; -3) и K(5; -11).
A) (5; 3)
B) (2; 4)
C) (5; -3)
D) (5; -2)
E) (-6; -3)
3.Отрезок АВ с координатами концов А (-11; 8) и В (3; 1) разбили точкой О в отношении 5:2, считая от точки А. Вычислите координаты точки О.
A) (1; 3)
B) (-2; 2)
C) (1; -2)
D) (-1; 3)
E) (-1; 2)
4.Разложить  по двум неколлинеарным векторам
по двум неколлинеарным векторам  и
и  .
.
A) 
B) 
C) 
D) 
E) 
5.Найдите значение числа р, если 


 и их скалярное произведение равно
и их скалярное произведение равно  . Под каким углом располагаются вектора
. Под каким углом располагаются вектора  и
и  ?
?
A) 90°
B) 180°
C) 60°
D) 120°
E) 150°
6. Найти  , если
, если  = 11,
= 11,  = 23, и
= 23, и  = 30
= 30
A) 20
B) 19
C) 22
D) 18
E) 21
тема: Декартовы координаты
Уровень «А»
1.Составьте уравнение окружности с центром в точке А и радиусом R, если А(-2;-3) и R=4.
А) (х-2)2+(у-3)2=16
В) (х-2)2+(у+3)2=42
С) (х+2)2+(у+3)2=4
Д)(х+2)2+(у+3)2=16
Е)  у+3)=16
у+3)=16
2.АВСD прямоугольник. Найдите координаты т. А, если В(3;8), С(7;-4) и D(1;-6).
A) (3;-6)
B) (-2;4)
C) (-3;6)
D) ( 3;-4)
E) (-2;6)
3. Найдите площадь квадрата АВСD, если А(3;5) и С(-3;-5).
A) 72
B) 64
C) 66
D) 68
E) 81
4. В круг вписан квадрат, у которого известны вершины: В(9;9) и D(-1;3).
Найдите центр окружности.
A) (4;8)
B) (2;5)
C) (3;8)
D) (-4;-6)
E) (4;6)
5. Окружность задана уравнением х2 – 10х + у2 + 8у + 16 = 0. Найдите координаты точек пересечения окружности с осью абсцисс.
A) (2;0), (8;0)
B) (-2;0), (6;0)
C) (3;0), (9;0)
D) (2;0), (-6;0)
E) (-2;0),(-8;0)
6. Найдите площадь ромба, если известны две его вершины: А(7;10;) и С(-5;-6), а длина одной из диагоналей равна 10.
A) 120
B) 110
C) 80
D) 90
E) 100
7. Найдите длину большей диагонали ромба с вершинами А(-10; -1), В(-5; 9), С(6; 7) и Д(1; -3).
A) 30
B) 16
C) 6
D) 10
E) 
Уровень «В»
1.Найдите площадь ромба с вершинами А(-10;-1), В(-5;9), С(6;7) и D(1;-3).
A) 128
B) 144
C) 120
D) 118
E) 136
2. Найдите длину большей диагонали ромба с вершинами А(-8;0), В(-4;7), С(4;6) и D(0;-1).
A) 9
B) 6
C) 8
D) 10
E) 6
3. Определите косинус угла А треугольника АВС, если его вершины имеют координаты: А(1;7), В(3;3), С(-5;1)
A) 
B) 
C) 
D) 
E) 
4. Найдите площадь треугольника с вершинами: А(-12;-2), В(20;-6) и С(-4;10).
A) 244
B) 144
C) 156
D) 208
E) 302
5. Отрезок АВ поделён точками Р и К на 3 отрезка, длины которых пропорциональны числам 1: 2: 1. Найдите координаты точки К, если А(-8;-5) и В(8;7).
A) (-3;4)
B) (-4;-3)
C) (3;4)
D) (4;4)
E) (3;-4)
6. Найдите координаты точек пересечения прямой у = – х + 8 и окружности  .
.
A) (0; 8) и (8; 0)
B) (0; 7) и (7; 0)
C) (0; 6) и (6; 0)
D) (0; – 7) и (– 7; 0)
E) (0; 4) и (4; 0
7. Составить уравнение окружности, описанной около треугольника, стороны которого лежат на прямых: x = 0, y = 0, 3x + 4y – 12 = 0
A) (x – 1,5)2 + (y – 2)2 = 6,25
B) (x – 2)2 + (y – 2)2 = 4
C) (x – 3)2 + (y – 4)2 = 12
D) (x – 2)2 + (y – 1,5)2 = 6,25
E) (x – 1)2 + (y – 1)2 = 1
Уровень «С»
1.Определите длину медианы АМ треугольника с вершинами А(-2;8), В(6;2) и С(2;-6).
A) 
B) 
C) 
D) 
E) 
2. Найдите центр тяжести треугольника АВС, если его вершины А(-4;10 ), В(2;8 ),С(-4;-6 ).
A) (-2;4)
B) (-4;2)
C) (-1;2)
D) (1;3)
E) (-2;3)
3.Найдите координаты точек пересечения окружностей с радиусами равными 5 см, с центрами в точках (0;0) и (7;-7)
A) (4;3), (-3;4)
B) (-3;-4), (-4;-3)
C) (-3;-4), (3;4)
D) (3;3), (4;4)
E) (4;-3), (3;-4)
4.В прямоугольном треугольнике АВС из прямого угла С проведена биссектриса СК. На какие отрезки она разбивает сторону АВ, если известны координаты вершин: А(13;-4), В(-11;-11) и С(1;5).
A)  и
и 
B)  и
и 
C)  и
и 
D)  и
и 
E)  и
и 
5.В треугольнике с вершинами А(-7;-3), В(14;0) и С(-4;6) проведена медиана СК. Вo сколько раз медиана короче стороны АВ.
A) в 2
B) в
C) в 1,5
D) в 
E) в 3
6.Медиана СМ треугольника АВС в 2 раза короче стороны АВ. Найдите значение числа р, если А(-6;-3), М(3;-1) и С(р;6)
A) - 4 и 6
B) - 9 и 3
C) - 3 и 9
D) -6 и 4
E) 3 и 9
7.Найдите точки пересечения окружности с центром в точке (3,4), радиусом
равным 5 и прямой линией, заданной уравнением: х + у - 8=0.
A) (7;-1), (-8;0)
B) (-1;-7), (0;-8)
C) ( 1;-7), (8;0)
D) (-1;7), (0;8)
E) (0;8), (7;1)
8.Треугольник с вершинами А(-6;-1), В(10;-3) и С(-2;5) вписан в круг. Найдите площадь этого круга.
A) 64π
B) 63π
C) 65π
D) 67π
E) 66π

 Получите свидетельство
Получите свидетельство Вход
Вход



 см. Вычислите сумму катетов треугольника.
см. Вычислите сумму катетов треугольника.
 см
см см
см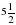 см
см  см
см см
см
 см, 5 см и 10 см?
см, 5 см и 10 см? 
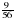

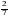










 Тесты по планиметрии (7-9 классы) (0.47 MB)
Тесты по планиметрии (7-9 классы) (0.47 MB)
 0
0 2176
2176 244
244 Нравится
0
Нравится
0





