Тема: Теорема Пифагора. Дата____________
Тип урока: изложение нового материала.
Используемые методы: активное слушание, запись в тетрадях, индивидуальная работа.
Используемые методы оценивания: словесная оценка (устная обратная связь), формативный опрос, «Светофор».
Оборудование: доска, тетради, ручки, линейки, карандаши, рисунки, карточки «Светофора», плакат с цитатой Пифагора, фото Собора Парижской Богоматери.
| Цели урока: Образовательная: познакомиться с теоремой Пифагора и её практическим применением. Воспитательная: воспитать навыки работы в коллективе. Развивающая: способствовать развитию памяти, интереса к искусству. | Индикаторы: |
| В результате изучения нового материала учащиеся смогут:
| Учащиеся в конце урока умеют:
|
Ход урока.
Орг. момент.
Актуализация знаний.
Новая тема.
Решение практических задач.
Историческая справка.
Домашнее задание.
Итог урока.
Орг. момент.
Проверка готовности учащихся к уроку.
Цели урока:
Знакомство с теоремой Пифагора.
Практическое применение теоремы Пифагора к решению геометрических задач.
Эпиграф.
Начать наш урок я хочу с сонета франко-немецкого писателя Шамиссо
«Пребудет вечной истина, как скоро
Ее познает слабый человек!
И ныне теорема Пифагора
Верна, как и в его далекий век.»
Актуализация знаний.
Вопросы для повторения.
Какой четырехугольник называется квадратом?
Как найти площадь квадрата?
Какой треугольник называют прямоугольным?
Как называются стороны прямоугольного треугольника?
Как найти площадь прямоугольного треугольника?
Задача. Найдите площадь треугольника АВС, если угол А=600, АВ = 14 см, ВС = 8 см.
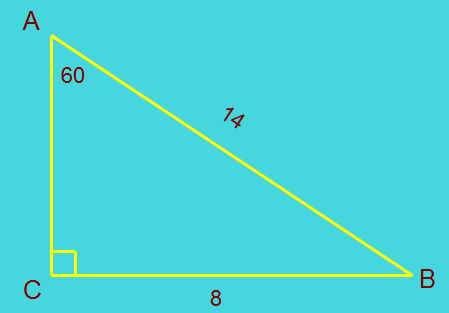
Дано: АВС – прямоугольный треугольник
C = 900; A = 600
АВ = 14 см, ВС = 8 см
Найти: SABC - ?см2
Решение: 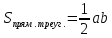 . Сумма углов треугольника равна 1800. Значит. B = 1800 – (900 + 600).Т.к.B = 300, то
. Сумма углов треугольника равна 1800. Значит. B = 1800 – (900 + 600).Т.к.B = 300, то 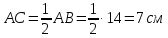 .
.
Найдем площадь 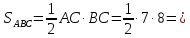 28 см2.
28 см2.
Ответ:  28 см2.
28 см2.
Новая тема.
Теорема Пифагора. В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов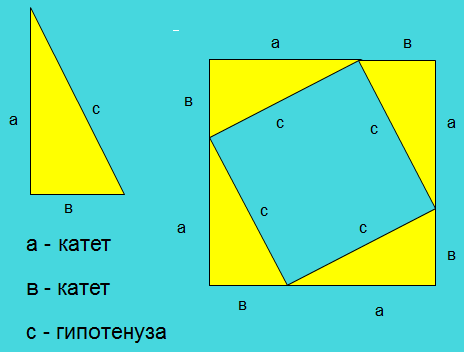
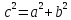
С помощью теоремы Пифагора можно решать два вида задач:
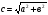 1. Найти гипотенузу прямоугольного треугольника, если известны катеты.
1. Найти гипотенузу прямоугольного треугольника, если известны катеты.
2. Найти катет, если известна гипотенуза и другой катет.
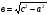
Решение практических задач.
В чем же причина популярности теоремы Пифагора? Красота! Простота! И значимость в практическом применении….
Давайте, решив задачи, узнаем, какой стиль архитектуры использовался в Древнем Египте при строительстве!
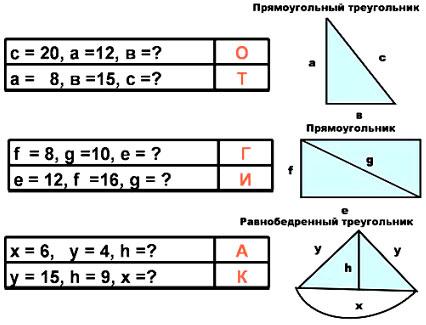
Заполните таблицу
| Ответ | 6 | 16 | 17 | 20 | 24 | 5 |
| Буква | г | о | т | и | к | а |
Показать Собор Парижской Богоматери

Историческая справка.
Удобный и очень точный способ, употребляемый землемерами для проведения на местности перпендикулярных линий, был известен с древних времён. Этот способ, по-видимому, применявшийся ещё тысячелетия назад строителями египетских пирамид, основан на том, что каждый треугольник, стороны которого относятся как 3:4:5, согласно теореме Пифагора - прямоугольный, так как 32 + 42 = 52. 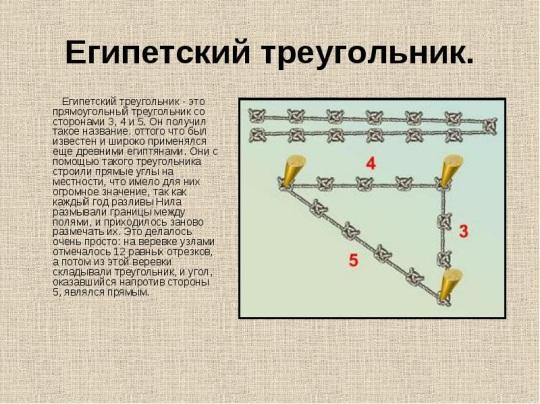
Поэтому треугольник с катетами 3, 4 и гипотенузой 5 называют “египетским” (на доске плакат «Египетский треугольник»).
Плакат с цитатой Пифагора.

Домашнее задание.
Подготовить презентацию в PowerPoint о жизни и деятельности Пифагора (5-7 слайдов):
Биография.
Пифагорейская школа.
Применение теоремы Пифагора.
Читать §3п.54-55; выполнять №486, 487
Итог урока:
Оценить работу класса и каждого ученика в отдельности (комментарии).
Выставить оценки в журнал и в дневники.
Проверить наличие записи Д/з в дневниках.

 Получите свидетельство
Получите свидетельство Вход
Вход












 Урок по геометрии "Теорема Пифагора" (439.2 KB)
Урок по геометрии "Теорема Пифагора" (439.2 KB)
 0
0 624
624 19
19 Нравится
0
Нравится
0



