Разработка урока геометрии в 8 классе согласно концепции компетентностного подхода
Морфологическая карта урока по теме «Теорема Пифагора»
| № | Тема урока | Жизненно-необходимая информация | Информация, которая встречается в других дисциплинах | Информация, которая нужна для дальнейшего изучения данной дисциплины (ВОУД, ЕНТ) | Информация для общего кругозора |
| 1 | Теорема Пифагора | уметь выполнять расчёты в строительстве, архитектуре при проектировании любых строительных объектов, при установке молниеотводов, при установке антенн мобильной связи.
Использовать знания для вычисления площадей треугольников, объёмов геометрических тел. | История, литература, стереометрия, уфология | ВОУД Решение задач по планиметрии, физике, задания по истории древнего мира. ЕНТ Стороны основания прямого параллелепипеда равны 2 дм и 7 дм, угол образованный ими 120 градусов. Вычислите площадь боковой поверхности параллелепипеда, если меньшая его диагональ равна 9 дм. 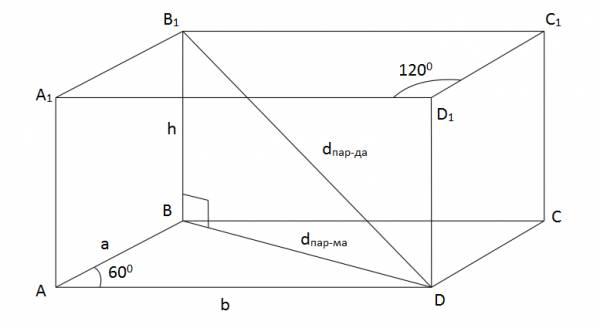 Пусть ABCDA₁B₁C₁D₁ прямой параллелепипед, основанием которого является параллелограмм. Стороны AB и AD обозначим как a и b соответственно. Площадь боковой поверхности можно вычислить по формуле: Sбок=Pпар-ма*hпар-да Высота параллелепипеда h найдется по теореме Пифагора в прямоугольном треугольнике B₁BD, меньшая диагональ основания BD найдется по теореме косинусов для треугольника ABD: Сторона треугольника BD по двум сторонам и углу между ними: d²пар-ма = a²+b²-2ab*cos(∠BAD)=2²+7²-2*2*7*cos(180-120)=4+49-28*cos60=53-14=39 h²=d²пар-да-d²пар-ма h²=9² - 39 = 81 - 39 = 42 h=√42 Sбок=Pпар-ма*hпар-да = 2*(2+7) * √42=18√42 | На данный момент в научной литературе зафиксировано 367 доказательств данной теоремы[8]. Вероятно, теорема Пифагора является единственной теоремой со столь внушительным числом доказательств. Такое многообразие можно объяснить лишь фундаментальным значением теоремы для геометрии. Разумеется, концептуально все их можно разбить на малое число классов. Самые известные из них: доказательства методом площадей, аксиоматические и экзотические доказательства (например, с помощью дифференциальных уравнений). В конце прошлого века Парижской академией наук была объявлена премия тому, кто первым установит связь с каким-нибудь обита¬телем другого мира. В шутку, хотя и не безосновательно, было предложено передать световой сигнал в виде чертежа • теоремы Пифагора, т.к. математический факт, выра¬жаемый ею, имеет место повсюду, и поэтому обитатели других миров должны понять этот сигнал. |
Сценарный план урока
Предмет: геометрия
Класс: 8
Тема: «Теорема Пифагора»
Цель урока: изучить теорему Пифагора и рассмотреть способы решения типовых задач.
Задачи:
Образовательная:
- исследовать закономерности между сторонами прямоугольного треугольника;
- изучить теорему Пифагора;
- формировать умения применять теорему Пифагора при решении задач;
Развивающая: способствовать развитию способности к сопоставлению, наблюдательности, внимания; развитие способности к аналитико-синтетическому мышлению, расширение кругозора;
Воспитательная: формирование потребности в знаниях, интереса к математике.
Предметные результаты:
Знать: формулировку теорему Пифагора;
Уметь: доказывать теорему Пифагора и применять её при решении задач
Межпредметные результаты:
- сформировать навыки использования ИКТ для организации учебной деятельности;
- представление исторических сведений по данной теме.
Тип урока: формирование новых знаний и умений.
Формы работы учащихся: фронтальная, индивидуальная, групповая.
Необходимое техническое оборудование: компьютер, интерактивное оборудование, программа «Живая геометрия».
Дидактические средства: учебник, электронная презентация, кружочки красные, зелёные, синие.
Методы и приемы: фронтальная работа, сочетающаяся с общеклассной; частично-поисковый метод; индивидуальная работа, работа парами.
Девиз урока: Покоряет вершины тот, кто к ним стремится.
Сценарий урока
Вводно-мотивационный этап.
Проверка настроения: приём “Мордашки” (у каждого ученика на столе 3 карточки, нужно показать ту, которая соответствует настроению).

На доске эпиграф урока «…Геометрия владеет двумя сокровищами:
Одно из них - это теорема Пифагора,
и другое - деление отрезков в среднем и
крайнем отношении…
Первое можно сравнить с мерой золота,
второе больше напоминает драгоценный камень»
Иоганн Кеплер.
2. Актуализация опорных знаний.
1. Работа в парах, выполнение теста с взаимопроверкой, анализ результатов тестирования.
1) Треугольник называется прямоугольным, если у него один из углов:
а) 45° б) 180° в) 60° г) 90°
2) Найдите прямоугольный треугольник :
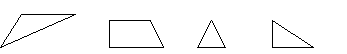
а) б) в) г)
3) Назовите прилежащий катет угла М в треугольнике КМР
М
К Р а) КР б) КМ в) РМ г) нет.
4) Какие из треугольников являются прямоугольными?

1 2 3 4 5
5) Чем является сторона АВ в треугольнике №2? _______________________
6) Какая сторона прямоугольного треугольника называется гипотенузой?
_________________________________________________________________
7) Чем являются стороны АС и ВС в треугольнике №2?
_________________________________________________________________
8) Какие стороны прямоугольного треугольника называются катетами?
__________________________________________________________________
5) На какие два многоугольника разбит данный многоугольник ABCFЕ?
 В С
В С
F
А E
D _________________________________
• Каким свойством площадей необходимо воспользоваться, чтобы найти площадь многоугольника ABCFЕ? ___________________________________
• С помощью, каких формул можно найти площадь квадрата и площадь треугольника? ______________________________________________________
3. Изучение новой темы. (10 мин.)
I. Создания проблемной ситуации.
Сказка – задача:
Давным-давно в некоторой стране жила прекрасная принцесса и была она настолько прекрасной, что затмевала красотой всех своих подруг и свою старшую сестру, которая красотой не блистала. Старшая сестра завидовала принцессе и решила ей отомстить. Тогда она пошла к ведьме и попросила её заколдовать принцессу. Ведьма не смогла ей отказать, но все же, ей стало жалко принцессу, поэтому ведьма придумала усыпить принцессу в башне до той поры, пока какой-нибудь принц не посмотрит на окно башни с такого места, чтобы расстояние от глаз принца до окна было 50 шагов.
И вот принцесса заснула крепким сном. Прошло много лет, но никто мне смог расколдовать принцессу, несмотря на то, что отец ее Король пообещал отдать принцессу в жены тому, кто спасет её от пут сна.
В один прекрасный день в этом городе появляется на белом прекрасном коне молодой принц. Узнав, какое несчастье произошло с принцессой, молодой принц берется расколдовать её. Для этого он измеряет длину от основания башни до окна, за которым скрывается принцесса. У него получается 30 шагов. Затем что-то прикидывает в уме и отходит на 40 шагов, поднимает голову и вдруг ... башня озаряется светом и через мгновенье навстречу принцу выбегает еще более прекрасная принцесса...
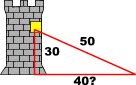
Как вы считаете, как же принц догадался, что от башни надо отойти на 40 шагов?
Учитель:
Что необходимо было знать принцу, чтобы освободить принцессу?
Учащиеся:
Для решения этой задачи необходимо знать соотношение между сторонами прямоугольного треугольника.
Проблема:
- найти соотношение между сторонами прямоугольного треугольника.
Для решения задачи нам нужны специальные формулы, связывающие между собой длины отрезков, площади, величины углов в фигурах. Такие формулы называют метрическими соотношениями. И, пожалуй, самое знаменитое из таких соотношений – теорема Пифагора. Она устанавливает простую зависимость между сторонами прямоугольного треугольника.
II. Теорема Пифагора.
III. Историческая справка. Представить себе эту теорему отдельно от имени великого грека невозможно (выступление ученика).


Воспитательный момент: доказательство теоремы Пифагора учащиеся средних веков считали очень трудным и называли его Dons asinorum - ослиный мост, или elefuga- бегство “убогих”,так как некоторые “убогие” ученики, не имевшие серьезной математической подготовки, бежали от геометрии. Слабые ученики, заучившие теоремы наизусть, без понимания, и прозваны по этому “ослами”, были не в состоянии преодолеть теорему Пифагора, служившую для них вроде непреодолимого моста. Из-за чертежей, сопровождающих теорему Пифагора, учащиеся называли ее так же “ветряной мельницей”, составляли стихи вроде “Пифагоровы штаны на все стороны равны”, рисовали карикатуры.
IV. Доказательство теоремы Пифагора.
На данный момент в научной литературе зафиксировано 367 доказательств данной теоремы. Вероятно, теорема Пифагора является единственной теоремой со столь внушительным числом доказательств. Такое многообразие можно объяснить лишь фундаментальным значением теоремы для геометрии.
Сегодня мы рассмотрим некоторые из них.
Учащиеся работают в группах (приём «джигсоу») с различными доказательствами теоремы. Данный вид деятельности подразумевает тьютерское сопровождение учителя.
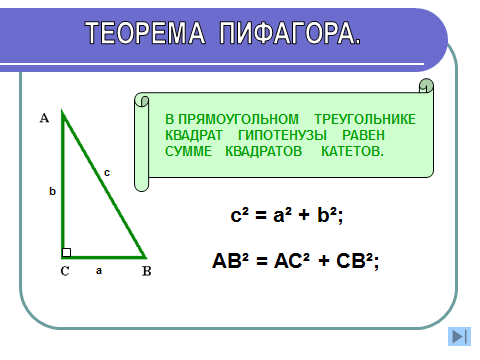
1 способ. Теорема. В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
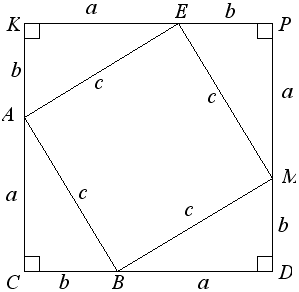
Дано: треугольник АВС – прямоугольный, АВ = с, ВС= b, АС = а, С =90°.
Доказать: с2 = а2 + b 2.
Доказательство:
а) Достроим треугольник АВС до квадрата СKPD со стороной (а+b );
SCKPD = (a+b)2 = a2 + 2ab + b2.
б) ABC = AKE = EPM = MDB по двум катетам.
SBCA = SAKE = SEPM = SMDB = ab.
в) ВАЕМ – квадрат, SBAEM = с2.
г) SCKPD = SBCA + SAKE + SEPM + SMDB+ SBAEM = 4 • ab + с2 = 2ab + с2.
a2 + 2ab + b2 = 2ab + с2;
с2 = а2 + b2 ч.т.д.
2 способ. Теорема. В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
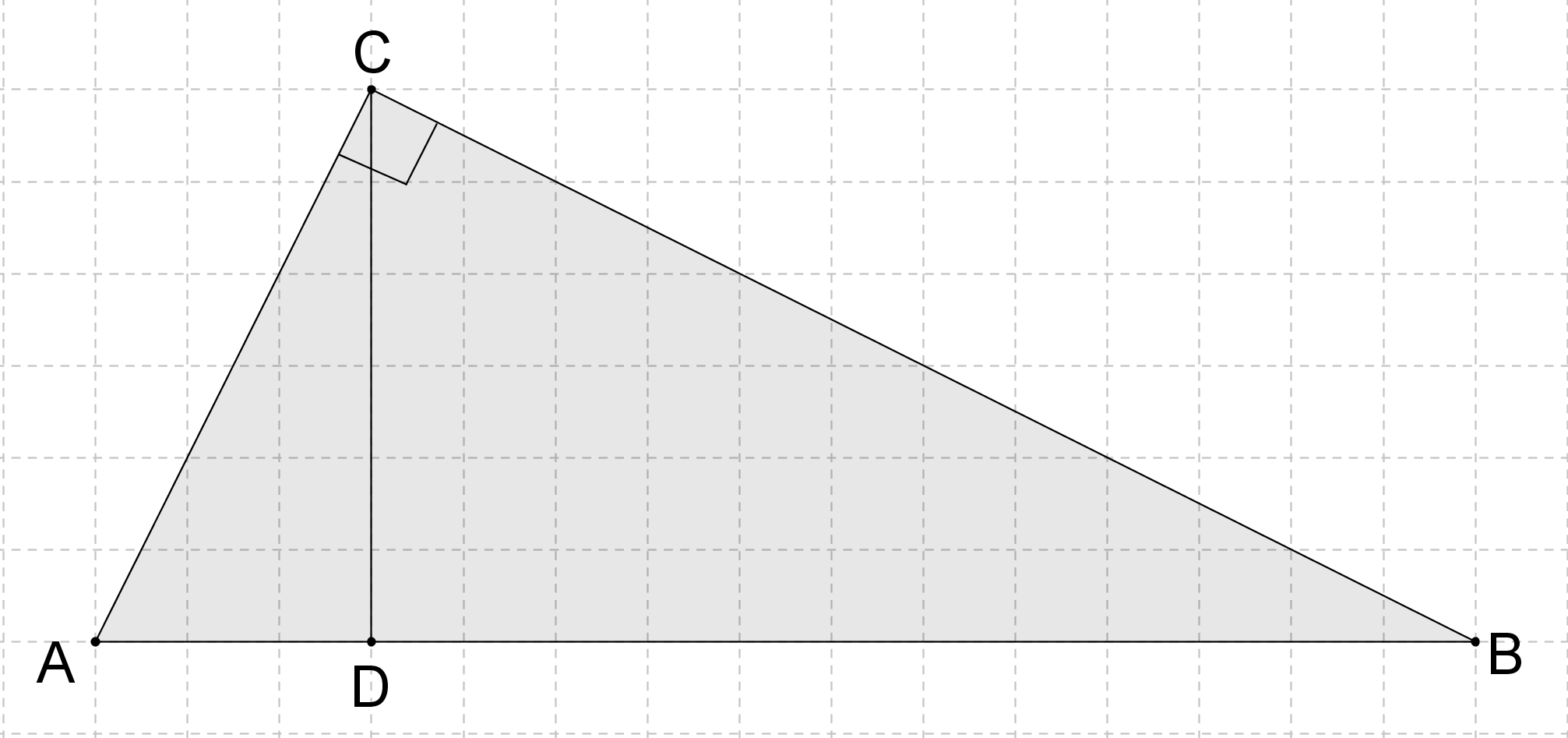
cos A = AC:AB; cos A = AD:AC
AC : AB = AD : AC; АС2 = АВ ∙ AD (1)
cos B = BC : AB; cos B = BD : BC.
BC : AB = BD : BC; BС2 = АВ ∙ BD (2)
АС2+ВС2 = АВ ∙ AD + АВ ∙ BD = AB ∙ (AD + BD) = AB ∙ AB = АВ2.
3 способ. Теорема. В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
П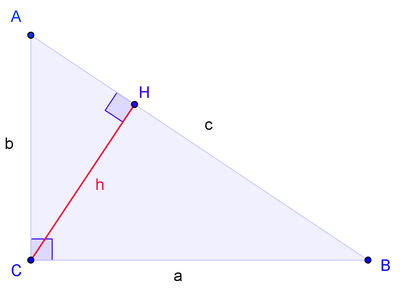 усть ABC есть прямоугольный треугольник с прямым углом C. Проведём высоту из C и обозначим её основание через H. Треугольник ACH подобен треугольнику ABC по двум углам. Аналогично, треугольник CBH подобен ABC. Введя обозначения
усть ABC есть прямоугольный треугольник с прямым углом C. Проведём высоту из C и обозначим её основание через H. Треугольник ACH подобен треугольнику ABC по двум углам. Аналогично, треугольник CBH подобен ABC. Введя обозначения
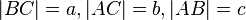
получаем
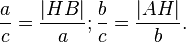
Что эквивалентно
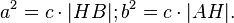
Сложив, получаем
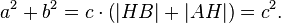
или
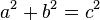 , что и требовалось доказать.
, что и требовалось доказать.
Вывод: Теорема Пифагора позволяет установить следующие соотношения, применяемые при решении задач:
а2 = с2 – b2;
b2 = с2 – а2.
Если дан нам треугольник,
И притом с прямым углом,
То квадрат гипотенузы
Мы всегда легко найдем:
Катеты в квадрат возводим,
Сумму степеней находим -
И таким простым путём
К результату мы придём.
V. Закрепление знаний. Применение теоремы Пифагора для решения практических задач (составление математической модели по условию задачи)
1 группа:
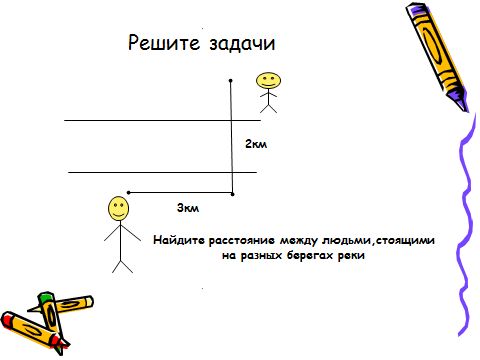
2 группа:

3 группа: Один конец каждого троса должен крепиться на высоте 12 м., другой на земле на расстоянии 5 м. от мачты. Хватит ли 50 м. троса для крепления мачты?
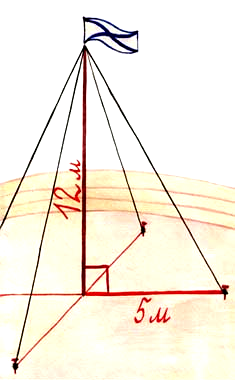
VI. Составление кластера «Теорема Пифагора»
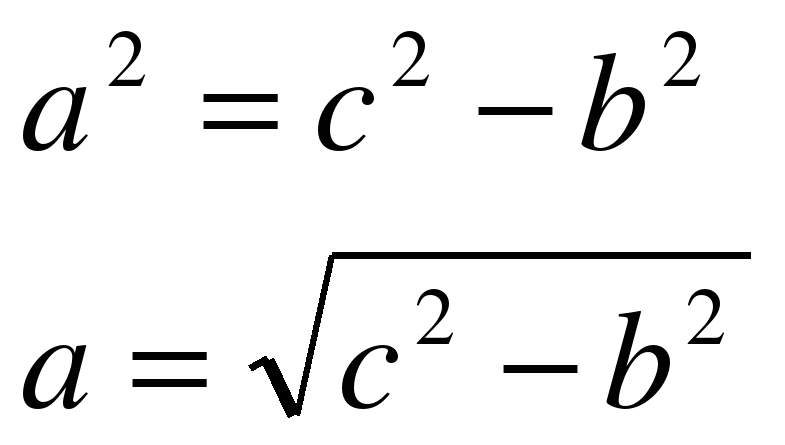


ТЕОРЕМА ПИФАГОРА




Значение История Устройство Алгоритм
Она показывает Установил Условие, Дано,
зависимость древне-греческий заключение доказать,
между гипотенузой учёный Пифагор доказательство
и катетами прямо- (VI век до н.э.)
угольного треугольника
VII. Рефлексивно-оценочный этап
Домашнее задание.
Решить задачу.
1 уровень. Необходимо обнести забором участок имеющий форму прямоугольного треугольника с катетами 8см и 15см. Как найти длину этой изгороди?
2 уровень. На обоих берегах реки растет по пальме, одна против другой. Высота одной 30 локтей, другой -20 локтей. Расстояние между их основаниями - 50 локтей.
На верхушке каждой пальмы сидит птица. Внезапно обе птицы заметили рыбу, выплывшую к поверхности воды между пальмами. Они кинулись к ней разом и достигли её одновременно.
На каком расстоянии от основания более высокой пальмы появилась рыба?
3 уровень. Докажи теорему Пифагора по чертежу
4 уровень. Изучи другие способы доказательства т. Пифагора.
Рефлексия Организация рефлексии на основе метода неоконченных предложений Ответь на 5 любых предложений.
Я почувствовал, что…
Было интересно…
Меня удивило…
Своей работой сегодня я…, потому что...
Мне захотелось…
Мне больше всего удалось…
Заставил задуматься…
Навел на размышления…
Сегодня я узнал…
Было трудно…, потому что...
Я выполнял задания…
Я понял, что…
Теперь я могу…, потому что...
Я приобрёл…
Я научился…
Задания для меня показались…, потому что...
Для меня было открытием то, что…
Мне показалось важным…, потому что...
Выставление оценок.
Учитель благодарит класс за работу и просит учеников поблагодарить друг друга за работу.
Приложение 1
Примеры заданий к уроку по теме «Теорема Пифагора» согласно таксономии Блума.
| Уровень | Навыки | Задания |
| Знание | Повторение или распознавание информации | Назовите …
В каком году …
Где происходит …
Напишите формулу …
Перечислите … |
| Понимание | Схватывание (понимание) смысла информационных материалов | Закончите фразу …
Что вы узнали …
Почему …
Преобразуйте выражение …
Объясните взаимосвязь …
Расскажите своими словами |
| Использование | Применение в сходной ситуации | Объясните цель применения
Решите домашнюю задачу несколькими способами …
Какая теория позволит объяснить данное явление
Проверьте предложенную гипотезу …
Выводы … |
| Анализ | Определить части и структуру | Какова структура …
Классифицируйте …
Что является следствием …
Сравните …
Проанализируйте причины … |
| Синтез | Соединить части по-новому | Найдите собственное решение …
Предложите алгоритм …
Найдите альтернативу …
Каковы возможные изменения …
Систематизируйте …
Исследуйте … |
| Оценка | Оценить значимость на основе критериев | Оцените логику …
Опишите достоинства …
Выделите критерии …
Соответствуют ли …
Что вы думаете о …
Сделайте выводы … |
Уровни АНАЛИЗ, СИНТЕЗ, ОЦЕНКА – соответствуют высокому уровню мышления.
| Знать | -элементы прямоугольного треугольника; -формулировку теоремы Пифагора; -алгебраическую запись теоремы Пифагора. |
| Понимать | - как найти связь между элементами треугольников, -как построить чертёж к решению задачи, -как построить математическую модель по условию задачи, -в чём заключается условие теоремы и её заключение. |
| Применять | -решать задачи на нахождение элементов прямоугольного треугольника |
| Анализировать | -составлять шаги алгоритма при решении заданий на нахождение элементов прямоугольного треугольника. |
| Оценивать | - оценивать свои результаты и результаты одноклассников; -оценивать оптимальность решения практических задач. |
| Творчество | Напишите эссе на тему «Я и теорема Пифагора», «Связь теоремы Пифагора с жизнью» |
Знание:
Вспомни формулировку теоремы Пифагора и сформулируй утверждения:
Катет — это ____________________ прямоугольного треугольника, образующих ___________ угол. (0-3 б)
В прямоугольном треугольнике ______________ катета (0-3 б)
Противоположная прямому углу сторона называется ____________.(0-3 б)
В прямоугольном треугольнике квадрат _____________ равен сумме квадратов катетов. (0-3 б)
Что выражают данные равенства: а) ; б) ;
в) ? (0-3 б)
Понимание:
Изобрази прямоугольный треугольник со катетами 6 см и 8 см. Составь таблицу и запиши на математическом языке связь между его элементами. (0-3 б)
Максимальное кол-во баллов за 1 и 2 уровень – 18 б
Применение:
Решите задачу.
Вертолет поднимается вертикально вверх со скоростью 4 м/с. Определите скорость вертолета, если скорость ветра, дующего горизонтально, равна 3 м/с.
Как далеко видно с маяка данной высоты над уровнем моря?
Вы плывёте на лодке по озеру и хотите узнать его глубину. Нельзя ли воспользоваться для этого торчащим из воды камышом, не вырывая его?
Решение.
Слегка отклонив камыш и держа его в натянутом состоянии, замерим расстояние а между точками А и В, в которых камыш пересекает поверхность воды соответственно в вертикальном и наклоненном положении. Возвратим камыш в исходное положение и определим высоту в над водой, на которую поднимется при этом точка В наклонённого камыша, заняв исходное положение С. Тогда обозначив через D основание камыша, а через х– искомую глубину АD, из прямоугольного  АВD по теореме Пифагора находим
АВD по теореме Пифагора находим
х2 +а2 = (х+в)2,
х2+а2= х2+2хв+в2
2хв=а2 – в2 ,
х= 
Пловец поплыл от берега реки, всё время гребя в направлении по перпендикуляру к берегу (берега реки считаем параллельными). Плыл он, приближаясь к противоположному берегу со скоростью 3 км/ч. Через 5 мин. он был на противоположном берегу. Узнайте, на каком расстоянии от мести начала заплыва он вышел на противоположном берегу, считая скорость течения всюду равной 6 км/ч.
Найдите площадь четырехугольника АВСD
Анализ:
Проанализируй теорему Пифагора и выдели в ней условие и заключение.
Сформулируй теорему обратную теореме Пифагора.
Объясни связь между теоремой Пифагора и теоремой косинусов.
Прямоугольные треугольники с целочисленными сторонами называют египетскими, а тройки целых чисел, для которых выполняется соотношение, связывающее стороны прямоугольного треугольника, – пифагоровыми тройками.
Проверь, являются ли пифагоровыми следующие тройки чисел:
3,4,5
5,12,13
7,24,25?
Придумай два-три примера египетских треугольников, стороны которых образуют пифагоровы тройки.
Синтез:
Напишите эссе на тему «Я и теорема Пифагора», «Связь теоремы Пифагора с жизнью»
Оценка:
Доказать с помощью теоремы Пифагора невиновность или виновность подозреваемого.
Этот эпизод взят из реальной следственной практики. Получив сообщение о краже, следователь выехал на место происшествия. Заявитель утверждал, что преступник проник в помещение, где хранились ценности, через окно. Осмотр показал, что подоконник находится на расстоянии 150 см от земли. Поверхность земли на расстоянии 200 см от стены здания покрыта густой порослью, не имевшей никаких следов повреждений. При осмотре не было найдено никаких технических средств типа лестницы. Возникло предположение, что преступник проникал в помещение через окно, каким-то образом преодолев расстояние между наружным краем поросли и подоконником. Оно было определено с помощью теоремы Пифагора. Следователь выдвинул версию об инсценировке кражи.
1. Проанализируйте ситуацию.
2. Выявите моменты, указывающие на возможность применения теоремы Пифагора.
3. На основании каких фактов следователь выдвинул версию о невиновности подозреваемого? Аргументируйте свой ответ.
4. Какие бы вы сделали выводы на месте следователя?

 Получите свидетельство
Получите свидетельство Вход
Вход







 В С
В С





 усть ABC есть прямоугольный треугольник с прямым углом C. Проведём высоту из C и обозначим её основание через H. Треугольник ACH подобен треугольнику ABC по двум углам. Аналогично, треугольник CBH подобен ABC. Введя обозначения
усть ABC есть прямоугольный треугольник с прямым углом C. Проведём высоту из C и обозначим её основание через H. Треугольник ACH подобен треугольнику ABC по двум углам. Аналогично, треугольник CBH подобен ABC. Введя обозначения












 Разработка урока геометрии по теме "Теорема Пифагора" (1.36 MB)
Разработка урока геометрии по теме "Теорема Пифагора" (1.36 MB)
 2
2 2985
2985 388
388 Нравится
0
Нравится
0


