Урок математики в 11 классе "Логарифмические уравнения"

Цели:

Ввести понятие иррациональных уравнений и показать способы их решений.

Развивать умение выделять главное, существенное в изучаемом материале, обобщать факты и понятия, развивать самостоятельность, мышление, познавательный интерес.

Содействовать формированию мировоззренческих понятий.

Оформление:

на доске плакат:

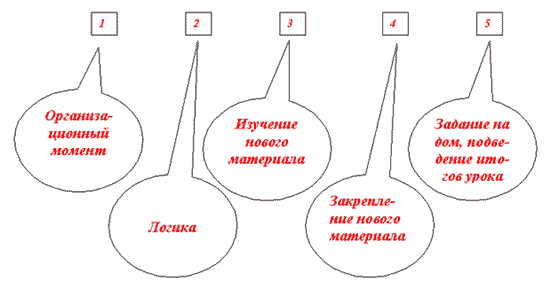
ПЛАН УРОКА:

высказывание: “Уравнение – это золотой ключ, открывающий все математические Сезамы”

вопрос: Подумайте, какой шаг в решении уравнения приводит к появлению лишних корней.

ХОД УРОКА

I. Организация и начало урока

Раз, два, три, четыре, пять

Начинаем мы считать

Бегать, прыгать мы не будем

Будем весь урок решать.

Учитель настраивает на урок и желает высоких результатов.

II. Постановка целей и задач урока, принятие их учащимися

Чтобы ответить на поставленный вопрос учащимся предлагается софизм.

Софизм – доказательство ложного утверждения, причем ошибка в доказательстве искусно замаскирована. Софистами называли группу древнегреческих философов IV-V веков до нашей эры, достигших большого искусства в логике.

Где допущена ошибка в следующей цепочке равенств?

16 – 36 = 25 – 45,

16 – 36 + 20,25 = 25 – 45 + 20,25,

(4 – 4,5)2 = (5 – 4,5)2,

4 – 4,5 = 5 – 4,5,

4 = 5,

2 . 2 = 5.

(Если квадраты двух выражений равны, то их основания либо равны между собой, либо противоположны.)

III. Изучение нового материала.

Уравнения, в которых переменная содержится под знаком корня, называются иррациональными.

Устно: какие из следующих уравнений являются иррациональными:

а) x + = 2,

б) = 11 + x,

в) ,

г) = 3,

д) y2 – 3y = 4.

Посредством уравнений, теорем

Он уйму всяких разрешал проблем.

И засуху предсказывал, и ливни –

Поистине его познания дивны.

Госер

IV. Алгоритм решения уравнений

1. Решение иррациональных уравнений сводится к переходу от иррационального к рациональному уравнению путем возведения в степень обеих частей уравнения или замены переменной.

2. При возведении обеих частей уравнения в четную степень возможно появление посторонних корней. Поэтому при использовании указанного метода следует проверить все найденные корни подстановкой в исходное уравнение.

3. Иногда удобнее решать иррациональные уравнения, определив область допустимых значений неизвестного и используя равносильные переходы.

Является ли число x корнем уравнения:

а) , x0 = 4;

б) , x0 = 2;

в) , x0 = 6;

г) , x0 = 0;

Решим уравнение:

Решение:

возведем обе части уравнения в квадрат:

x + 2 = x2,

x2 – x – 2 = 0,

x1 = – 1,

x2 = 2.

Проверка:

1) x = –1, тогда 1 = – 1 ложно;

2) x = 2, тогда , 2 = 2 верно.

Ответ: x = 2;

Решим уравнение: +1 – 2x = 0

Решение:

= 2x – 1,

x2 + 5x + 1 = (2x – 1)2

x2 + 5x + 4 = 4x2 – 4x + 1,

x (x – 3) = 0,

x1 = 0,

x2 = 3.

Проверка:

x1 = 0, то + 1 – 2 . 0 =/= 0, значит, x1 = 0, не удовлетворяет уравнению.

x2 = 3, тогда +1 – 2 . 3 = 0, значит x2 = 3 корень уравнения.

Ответ: x = 3.

Решим уравнение:

Решение: возведя обе части уравнения в квадрат, получим:

2x – 3 = x – 2, x = 1.

Проверка: – обе части уравнения не имеют смысла

Ответ: корней нет.

Решим уравнение:

Решение: поскольку корни арифметические, то левая часть уравнения неотрицательна, а правая отрицательна, значит, уравнение решений не имеет.

Ответ: уравнение решений не имеет.

V. Закрепление изученного материала.

№ 417 (а);

№ 418 (а; б);

№ 419 (а; г).

VI. Задание на дом.

№ 417 (в);

№ 418 (в; г);

№ 419 (б; в);

№ 422 (а; г).

VII. Подведение итогов урока.