Решение логарифмических уравнений и неравенств (презентация)

Цель:

учиться выбирать соответствующий метод решения логарифмических уравнений и неравенств.

применять выбранный метод

Задачи:

1. Повторить:

Определение логарифма, приемы его использования

Свойства логарифмов

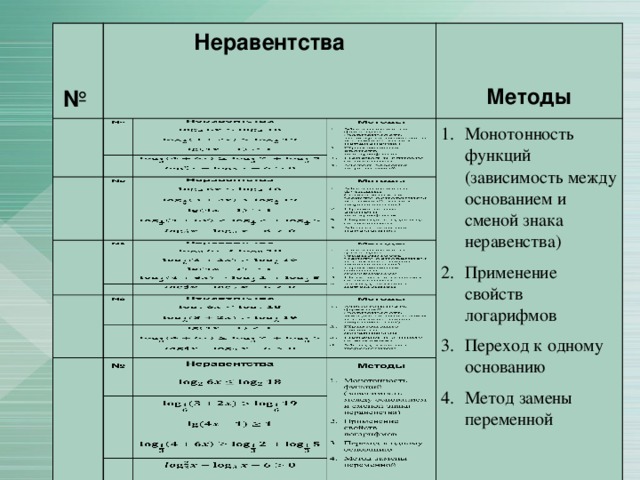
Методы решения логарифмических уравнений и неравенств

2. Решать уравнения и неравенства на основе различных методов

3. Рассмотреть использование логарифмов в природе и в различных сферах жизнедеятельности человека

Средства обучения:

Информационные:

Алгебра. 10 класс: учеб. для общеобразоват. учреждений / [Ю.М. Колягин и др.]. М.: Просвещение, 2015.

Математика, 11 класс, ПОДГОТОВКА К ЕГЭ 2015: учебно-методическое пособие/ под ред. Ф.Ф.Лысенко, С.Ю.Кулабукова. – Ростов-на-Дону: Легион-М,2015.(ЕГЭ-11)

Технические и программные:

компьютер;

мультимедийный проектор;

презентация MS Power Point.

Тип урока: закрепление и совершенствование знаний

Несложный, уровень трудности базовый

Формы учебной работы:

фронтальная,

парная,

индивидуальная работа по уровням сложности заданий.

Резерв: дифференцированные задания.

Содержательно-деятельностный компонент (ход урока):

1. Организационный момент.

Вступительное слово учителя: приветствие, работа по целеполаганию, определение задач урока.

Создание эмоционального настроя.

Организует проблемную ситуацию:

А можно ли решать логарифмические уравнения только на основе определения? Почему?

2. Самостоятельная работа с самопроверкой (тест)

Организует практическую деятельность обучающихся по выявлению ошибок вычисленных логарифмов, представленных на с лайде

Слайд №8

Анализ ошибок, обсуждение решений.

Организует обсуждение результатов практической работы: указание ошибок, обоснование правильного ответа

Слайд №9

3. Экспресс-опрос по методам решения логарифмических уравнений.

Организует обсуждение выбора методов решения логарифмических уравнений с выходом на обобщение в форме алгоритма действий

Слайд №11

Индивидуальная по уровням сложности заданий.

Организует практическую деятельность обучающихся по решению логарифмических уравнений с выбором методов.

4. Экспресс-опрос по методам решения логарифмических неравенств.

Организует обсуждение выбора методов решения логарифмических неравенств с выходом на обобщение в форме алгоритма действий

Слайд №14

5. Фронтальная работа по решению логарифмических неравенств.

Организует практическую деятельность обучающихся по решению логарифмических неравенств с выбором методов, учитывая монотонность функции

Сообщения о применении логарифмов в природе и в различных сферах жизнедеятельности человека.

организует презентации сообщений учеников о применении логарифмов в природе и в различных сферах жизнедеятельности человека, иллюстрируя материал с помощью слайдов

Приложение №1.

К слайдам № 17-30

Подведение итогов урока.

Фиксируется степень соответствия поставленной цели и результатов деятельности;

Приложения

Слайд №8-9

Самостоятельная работа с самопроверкой (тест) на приз Непера

Немного об изобретателе логарифмов и создателе логарифмических таблиц (слайд 10).

Джон Непер – шотландец. В 16 лет отправился на континент, где в течение пяти лет в различных университетах Европы изучал математику и другие науки. Затем он серьезно занимался астрономией и математикой. К идее логарифмических вычислений Непер пришел еще в 80-х годах XVI в., однако опубликовал свои таблицы только в 1614 г., после 25-летних вычислений! Они вышли под названием “Описание чудесных логарифмических таблиц”. Неперу принадлежит и сам термин “логарифм”, который он переводит как “искусственное число”. Таблицы и идеи Непера быстро нашли распространение. “Правило Непера” и “Аналогии Непера” можно встретить в так называемой сферической тригонометрии.

Слайд №11

Задание на нахождение идеи решения уравнения. Необходимо сопоставить уравнение, прием для решения уравнения.

Слайд №14

Экспресс-опрос.

Задание на нахождение идеи решения неравенства. Необходимо сопоставить неравенство, прием для его решения.

Для каждого неравенства с 1 по 5 определить основание и установить зависимость между основанием и сменой знака неравенства

Приложение № 1

Сообщения обучающихся

Логарифмы в природе и в различных сферах жизнедеятельности человека.

Яркость звезд. Астрономы распределяют звезды по степеням видимой яркости на светила первой величины, второй величины, третьей и т.д. Последовательные звездные величины воспринимаются глазом, как члены арифметической прогрессии. Но физическая яркость их изменяется по иному закону: объективные яркости составляют геометрическую прогрессию со знаменателем 2,5. Легко понять, что «величина» звезды представляет собой не что иное, как логарифм ее физической яркости. Оценивая видимую яркость звезд, астроном оперирует с таблицей логарифмов, составленной по основанию 2,5 (по договоренности между астрономами всего мира в настоящее время принимается, что блеск звезды 1-й величины в 2,5 раза превосходит блеск звезды 2-ой величины).

Например, на сетчатку проецировался синий цвет, однако на периферию сетчатки он не попадает, так как там всегда «нуль-цвет». Синий цвет сравнивается с «нуль - цветом» и мгновенно вырабатываются сведения о разности логарифмов чисел – сигналов, и наш мозг выполняет команду выработать синий цвет.

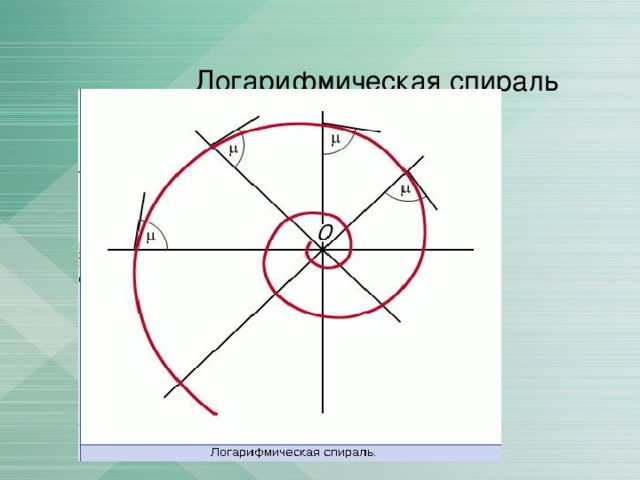
Логарифмическая спираль. В математике существует понятие логарифмической спирали. Спираль – это плоская кривая линия многократно обходящая одну из точек на плоскости, эта точка называется полюсом спирали. Полюсом логарифмической спирали является начало координат. Спираль называется логарифмической, потому что уравнение, описывающее эту спираль, содержит логарифмы. Эта спираль имеет бесконечное множество витков, она не проходит через свой полюс. Логарифмическую спираль называют равноудаленной спиралью, это связано с тем, что в любой точке логарифмической спирали угол между касательной к ней и радиус – вектором сохраняет постоянное значение.

Раковина улитки. Немецкий биолог Румблер в 1910 году выдвинул теорию постоянного краевого угла при построении раковин улиток. Он исходил из того, что материал, из которого строятся раковины, вначале должен быть жидким, и в жидком состоянии попадает на край уже существующей части раковины где, естественно, всегда образуется постоянный краевой угол. Под этим углом жидкость затвердевает, и снова начинается та же игра. Раковина улитки представляет собой логарифмическую спираль.

Полет бабочки. Ночные бабочки, которые пролетают большие расстояния, ориентируясь по параллельным лунным лучам, инстинктивно сохраняют постоянный угол между направлением полета и лучом света.

Если они ориентируются на пламя свечи, то инстинкт их подводит, и бабочки попадают в пламя по скручивающейся логарифмической спирали.

Звездные галактики. 1845 г. английский астроном лорд Росс (Уильям Парсонс) с помощью телескопа со 180-сантиметровым металлическим зеркалом обнаружил целый класс туманностей в виде логарифмической спирали, самым ярким примером которых явилась туманность в созвездии Гончих Псов. Природа этих туманностей была установлена лишь в первой половине XX столетия. Спиральные туманности - это огромные звездные системы, сравнимые с нашей Галактикой. С тех пор их и стали называть галактиками. Немало усилий пришлось приложить астрономам, чтобы описать свойства спиральных галактик с помощью логарифмов. В спиральных ветвях наблюдается повышение плотности, как звезд, так и межзвездного вещества - пыли и газа. Повышенная плотность газа ускоряет образование и последующее сжатие газовых облаков и тем самым стимулирует рождение новых звезд. Поэтому спиральные ветви являются местом интенсивного звездообразования.

Радиоактивный распад. Изменение массы радиоактивного вещества происходит по формуле содержащей логарифм слайд 27

Формула Циолковского. Эта формула, связывающая скорость ракеты V с ее массой m:, где  Vr – скорость вылетающих газов, m₀ – стартовая масса ракеты. слайд 29

Скорость истечения газа при сгорании топлива Vr невелика (в настоящее время она меньше или равна 2 км/с). Логарифм растет очень медленно, и для того чтобы достичь космической скорости, необходимо сделать большим отношение   т.е. почти всю стартовую массу отдать под топливо.

Звукоизоляция стен. Коэффициент звукоизоляции стен измеряется по формуле, слайд 30 где p₀ – давление звука до поглощения, p – давление звука, прошедшего через стену, А – некоторая константа, которая в расчетах принимается равной 20 децибелам.

Если коэффициент звукоизоляции D равен, например 20 децибел, то это означает, что  и p₀ =10p, т.е. стена снижает давление звука в 10 раз. Такую изоляцию имеет деревянная дверь.

Потому-то, словно пена Опадают наши рифмы И величие степенно  Отступает в логарифмы Борис Слуцкий

Логарифмические уравнения и неравенства

Цель:

• учиться выбирать соответствующий метод решения логарифмических уравнений и неравенств
• применять выбранный метод

Задачи:

1. Повторить:

• Определение логарифма
• Свойства логарифмов
• Методы решения логарифмических уравнений и неравенств

2. Выработать алгоритм решения логарифмического уравнения и неравенства

3. Рассмотреть использование логарифмов в природе и в различных сферах жизнедеятельности человека

Определение логарифма

Основные формулы

0,b0,c0, c≠1,n ≠1   " width="640"

Свойства логарифмов .

Основное логарифмическое

тождество

Основные

a0,b0,c0, c≠1,n ≠1

Самостоятельная работа с самопроверкой

1

1

2

2

3

=7

3

4

4

5

5

6

= 0

6

7

7

8

8

9

9

10

10

Самопроверка

1

+

2

-

3

+

4

-

5

+

6

+

7

-

8

+

9

+

10

-

Непер Джон (1550-1617 гг.) - шотландский математик, изобретатель логарифмов.

1

1

2

2

№

№

3

3

1.На основе определения логарифма

Уравнение

1.На основе определения логарифма

Уравнение

2. Применение свойств логарифмов

4

2. Применение свойств логарифмов

4

Методы

Методы

5

5

3. Переход к одному основанию

3. Переход к одному основанию

6

6

4. Метод замены переменной

4. Метод замены переменной

7

7

8

8

9

9

Внимание!

1. Найти ОДЗ

исходного уравнения

2. Выбрать соответствующий метод и решить уравнение

3. Выбрать корни

с учетом ОДЗ

Неравентства

Неравентства

№

№

• Монотонность функций (зависимость между основанием и сменой знака неравенства)
• Применение свойств логарифмов
• Переход к одному основанию
• Метод замены переменной

• Монотонность функций (зависимость между основанием и сменой знака неравенства)
• Применение свойств логарифмов
• Переход к одному основанию
• Метод замены переменной

Методы

Методы

Внимание!

1. Найти ОДЗ

исходного неравенства

2. Выбрать соответствующий метод и решить неравенство, учитывая монотонность функции

3. Выбрать решения с учетом ОДЗ

Логарифмы в природе и в различных сферах жизнедеятельности человека

Логарифмическая спираль

Логарифмическая спираль

Рога таких животных, как архары, закручены по логарифмической спирали.

В подсолнухе семечки расположены по дугам, близким к логарифмической спирали

Бивни слонов и вымерших мамонтов, когти львов и клювы попугаев являют собой логарифмические формы и напоминают форму оси, склонной обратиться в спираль.

Пауки всегда плетут свои паутины в виде логарифмической спирали.

Строение таких микроорганизмов, как планктоны также имеют форму спирали.

Логарифмическая спираль

Раковины морских животных могут расти лишь в одном направлении. Чтобы не слишком вытягиваться в длину, им приходится скручиваться, причем каждый следующий виток подобен предыдущему. А такой рост может совершаться лишь по логарифмической спирали или ее аналогиям. Поэтому раковины многих моллюсков, улиток, закручены по логарифмической спирали.

Полет бабочки

Звездные галактики

По логарифмической спирали формируется и тело циклона

Температурный коэффициент химической реакции в технологии производства оптоволокна равен наибольшему целому решению неравенства

Благодаря распространению оптоволоконной технологии обычные пользователи сегодня могут наслаждаться высокоскоростным интернетом .

Период полураспада

β – частицы в процессе движения по

траектории светоизлучения

равен наибольшему целому решению

неравенства

В сейсмологии:

При вычислении магнитуды.

Магнитуда землетрясения — величина, характеризующая энергию, выделившуюся при землетрясении в виде сейсмических волн .

Формула Циолковского

Эта формула, связывающая

скорость ракеты V с ее массой m

,

Звукоизоляция стен Коэффициент звукоизоляции стен измеряется по формуле, где p 0  – давление звука до поглощения, p – давление звука, прошедшего через стену, А – некоторая константа, которая в расчетах принимается равной 20 децибелам.  Если коэффициент звукоизоляции D равен, например 20 децибел, то это означает, что  и p 0  =10p, т.е. стена снижает давление звука в 10 раз. Такую изоляцию имеет деревянная дверь.

Потому-то, словно пена Опадают наши рифмы И величие степенно  Отступает в логарифмы Борис Слуцкий