Урок математики в 10 классе по теме: «Решение тригонометрических уравнений»

Урок математики в 10 классе по теме: «Решение тригонометрических уравнений» разработала

Зезюлина Лариса Леонидовна, учитель математики МБОУ Витемлянская СОШ

Погарского района Брянской области.

Тема: Решение тригонометрических уравнений

Урок обобщения и систематизации знаний

Цели урока:

- повторить, обобщить и систематизировать материал темы. Выполнить контроль усвоения знаний и умений.

-способствовать формированию умений применять приемы: сравнения, обобщения, выделения главного ,,переноса знаний в новую ситуацию, развитию математического кругозора, мышления и речи, внимания и памяти.

- содействовать воспитанию интереса к математике, ее приложениям, активности, мобильности, общей культуре, умению общаться.

Ход урока:

1.Организационный момент.

Сегодня у нас заключительный урок по теме «Решение тригонометрических уравнений». Мы повторим, обобщим и приводим в систему изученные виды, типы , методы и приемы решения тригонометрических уравнений.

Перед вами стоит задача- показать свои знания и умения по решению тригонометрических уравнений

2. Тест с самопроверкой

1.Каково будет решение уравнения cos x =а при 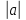˃ 1

2. При каком значении а уравнение cos x =а имеет решение

3.какой формулой выражается это решение

4. В каком промежутке находится аrc cos x а

5. В каком промежутке находится значение а

6. Каким будет решение уравнения cos x =1

7. каким будет решение уравнения cos x = -1

8. Каким будет решение уравнения cos x = 0

9.Чему равняется аrc cos x(- а)

10. Каким будет решение уравнения sin х =1

11.Каким будет решение уравнения sin х = - 1

12. Каким будет решение уравнения sin х = 0

13. Какой формулой выражается решение уравнения tg х = а

14. В каком промежутке находится arctg а

3. Систематизация теоретического материала:

Классификация тригонометрических уравнений.

На доске написаны уравнения и повешена системно обобщающая таблица. У чащиеся определяют тип и методы решения уравнения.

1. 3 sin² х – sinх соsх - 2соs² х =0

2. соs² х - 9 соsх +8 =0

3. sin6х – соs3х = 0

4. 2 соs² х +3sinх = 0

5. 2 sinх соsх = соs2х -2 sin² х

6. Соs2х +соs(π – х)= 0

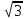7. соsх + sinх = 1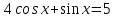

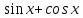8. 

9. = 1

Тригонометрические уравнения

Решение уравнений по известным алгоритмам решение уравнений путем разбиения

на подзадачи

одноименные уравнения и уравнения, решающиеся разложением

сводящиеся к ним на множители

уравнения вида асоsх + bsinх = с, а,b и с ǂ 0, решающиеся методом введения вспомогательного аргумента

4.Рассмотреть блоки уравнений и ответить на вопросы

1) а) sin =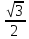

б)соs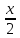 = а² + 1

в) tg(2х - ) =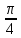

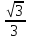
г) сtg3х = -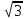

О чем идет речь.

Ответы:1,2,4 – простейшие тригонометрические уравнения

2)а) 2 sin2х + 5 sin2х -3 = 0

б)6sin² х+ 4 sinх соsх = 1

в)3tgх + 5сtgх = 8

г)2 sin²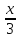 + 5соs 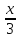+1 = 0

ответ: 1,3,4 – одноименные тригонометрические уравнения и сводящиеся к ним решаются методом подстановки

3) а)sinх +соsх = 0

б) sin² х-5 sinх соsх+ 4соs²х=0

в) 3 sinх соsх- соs²х=0

ответ: 1- однородное уравнение 1 степени решается делением на соsх ( sinх); 2- однородное уравнение второй степени решается делением на соs²х (sin² ); 3- нельзя делить на соs²х, это приведет к потере корней. Можно делить на 6sin² х или разложить на множители.

4) а) 2соs3х + 4sin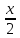 = 7

б) 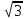соsх + sinх= 2

в) соsх + 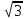sin х = 1

ответ: 2,3 –уравнения, решающиеся методом введения вспомогательного аргумента.

5. дифференцированная самостоятельная работа ( самопроверка)

На доске записаны задания трех уровней. Учащиеся выполняют задания того уровня, который он выбрал.

1 уровень. 1. 2 соs² х + 3sinх = 0

2. sin 2х + sinх = 0

2 уровень. 1. 2 sin² х + соs 2х = sin 2х

2. sin7х + соs4х = sin х

3 уровень. 1. Соs2х соsх = соs3х

2. 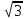соsх+ sinх = 2

Дополнительно: соs² х + соs² 2х + соs² 3х + соs² 4х= 2

Итог урока

Учащиеся отвечают на вопросы

1. Какие уравнения называются тригонометрическими

2. Какие типы и и методы решения тригонометрических уравнений вы знаете

Оценка работы класса

Домашняя работа.

Решить уравнения: sinх+ соsх = 0

3tgх + ctgх = 8

3sinхсоsх – соs² х =0