Цели:
Образовательные:
закрепить у учащихся знания о теле вращения – цилиндре (определение, элементы цилиндра, сечение цилиндра, формулы площади боковой и полной поверхности цилиндра);
сформировать навыки решения типовых задач;
Развивающие:
развитие навыков самоконтроля и взаимоконтроля;
развитие речи учащихся;
развитие творческого мышления учащихся;
личностное саморазвитие учащихся;
Воспитательные:
воспитание нравственных качеств личности, таких как аккуратность, дисциплинированность;
воспитание умения работать в коллективе.
Тип урока: урок - бенефис.
Оборудование: карточки с заданиями
Ход урока.
I. Организационный момент
Приветствие учителем учеников
Учитель: Сегодня весь урок мы посвятим обобщению знаний о площади поверхности цилиндра.
II. Теоретическая разминка.
(Учитель раздает листочки с заданиями, учащиеся заполняют и сверяют свои ответы с правильными, названными учителем)
Пример карточки
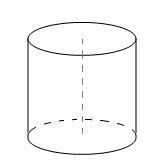
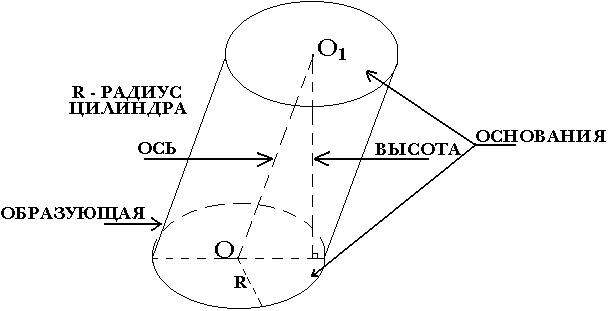
1. Нанесите на рисунок основные элементы цилиндра.
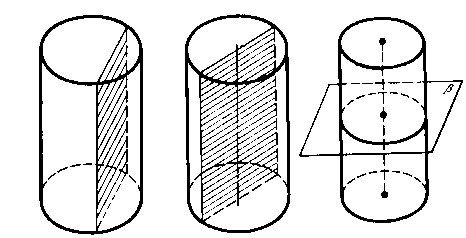
2. Изобразите а) осевое сечение цилиндра; б) сечение цилиндра плоскостью, проходящей перпендикулярно оси цилиндра; в) сечение цилиндра плоскостью, проходящей параллельно оси цилиндра. Какая фигура получается в каждом случае?
III. Математический диктант
(у учеников заранее приготовлены пустые листочки)
Учитель: достаем чистые листочки, подписываем их и приступаем к выполнению математический диктант
(учитель диктует вопросы учащимся)
Учитель: вопрос №1: Дайте определение цилиндра.
Учитель: вопрос №2: Как можно получить эту фигуру?
Учитель: вопрос №3 : Чему равна Sб цилиндра?
Учитель: вопрос №4: Что лежит в основании цилиндра?
Учитель: вопрос№5 : По какой формуле находится площадь круга?
Учитель: вопрос №6: Что получится при вращении прямоугольника вокруг одной из его сторон?
Учитель: вопрос №7:Что называется высотой цилиндра?.
Учитель: Сдаем листочки на проверку. А сейчас мы с вами заслушаем не большое сообщение.
IV. Историческая справка
(заранее подготовленная учеником)
Историческая справка
Слово цилиндр происходит от греческого слова , что означает “валик”, “каток”. Конус в переводе с греческого “konos” означает “сосновая шишка”. С конусом и цилиндром люди знакомы с глубокой древности. В 1906 году была обнаружена книга Архимеда (287–212 гг. до н. э. ) “О методе”, в которой дается решение задачи об объеме общей части пересекающихся цилиндров. Архимед приписывает честь открытия этого принципа – Демокриту (470–380 гг. до н. э. ) – древнегреческому философу - материалисту. С помощью этого принципа Демокрит получил формулу для вычисления объема пирамиды и конуса.
Много сделала для геометрии школа Платона (428–348 гг. до н. э. ). Платон был учеником Сократа (470–399 гг. до н. э. ). Он в 387 г. до н. э. основал в Африке Академию, в которой работал 20 лет. Каждый, входящий в Академию, читал надпись: “Пусть сюда не входит никто, не знающий геометрии”. Школе Платона с частности принадлежит: а) исследование свойств призмы, пирамиды, цилиндра и конуса; б) изучение конических сечений.
Большой трактат о конических сечениях был написан Аполлонием Пергским (260–170 гг. до н. э. ) – учеником Евклида (III в. до н. э. ), который создал великий труд из 15 книг под названием “Начала”. Эти книги издаются и по сей день, а в школах Англии по ним учатся до сих пор.
Цили́ндр (др. - греч. κύλινδρος — валик, каток) — геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими её. Цилиндрическая поверхность — поверхность, получаемая таким поступательным движением прямой (образующей) в пространстве, что выделенная точка образующей движется вдоль плоской кривой (направляющей). Часть поверхности цилиндра, ограниченная цилиндрической поверхностью, называется боковой поверхностью цилиндра. Другая часть, ограниченная параллельными плоскостями - это основания цилиндра. Таким образом, граница основания будет по форме совпадать с направляющей. Цилиндр - это тело полученное в результате вращения прямоугольника, относительно одной из его сторон.
В большинстве случаев под цилиндром подразумевается прямой круговой цилиндр, у которого направляющая — окружность и основания перпендикулярны образующей. У такого цилиндра имеется ось симметрии.
Другие виды цилиндра — (по наклону образующей) косой или наклонный (если образующая касается основания не под прямым углом); (по форме основания) эллиптический, гиперболический, параболический.
Призма также является разновидностью цилиндра — с основанием в виде многоугольника.
Весь материал - смотрите документ.

 Получите свидетельство
Получите свидетельство Вход
Вход


 .а)
.а) 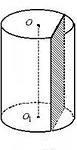









 Урок математики "Цилиндр. Площадь поверхности цилиндра" (0.17 MB)
Урок математики "Цилиндр. Площадь поверхности цилиндра" (0.17 MB)
 0
0 1693
1693 171
171 Нравится
0
Нравится
0




