Открытый урок учителя математики Яблонской З.Н.
11 класс 11.03.2014. г. Степногорск
Тема: Методы решения иррациональных уравнений.
Тип урока: Урок комплексного применения знаний.
Цели:
Образовательные:
повторить определение и основные методы решения иррациональных уравнений,
продемонстрировать нестандартные методы решения иррациональных уравнений,
формировать умение выбирать рациональные способы решения,
систематизировать, обобщить, расширить знания и умения связанные с применением методов решения иррациональных уравнений.
Развивающие: содействовать развитию математического мышления учащихся.
Воспитательные:
формировать гуманные отношения на уроке через работу в коллективе,
добросовестное отношение к учебному труду,
ответственность, честность, сопереживание успехам и неудачам товарищей,
побуждать учащихся к преодолению трудностей в процессе умственной деятельности.
Методы обучения:
Формы организации учебной деятельности:
Оборудование:
ПК
интерактивная доска
карточки для индивидуальной работы
карточки для построения графиков самоанализа своей деятельности на уроке
карточки с условием самостоятельной работы
Ход урока
I. Организационный момент
Основная задача – обеспечить нормальную внешнюю обстановку для работы на уроке и психологически подготовить учащихся к предстоящему занятию.
II. Этап проверки домашнего задания.
Ответы заранее приготовлены на доске, учащиеся самостоятельно проверяют Д/З и выставляют себе оценку на графике самоанализа.
III. Актуализация знаний.
Устная работа. Презентация. Опрос теоретического материала.
Сформулируйте определение иррационального уравнения. (слайд 1)
Определение. Уравнение с одной переменной называют иррациональным, если оно содержит переменную х под знаком корня или дробной степени.
Являются ли данные уравнения иррациональными? (слайд 2)
а) �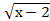 � +8=х
� +8=х
б) 1+х = х�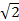 �
�
в) �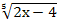 � = х+6
� = х+6
г) �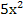 � + х�
� + х�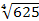 � = 0
� = 0
Что значит решить иррациональное уравнение?(слайд 3)
Решить уравнение – значит найти все его корни или доказать, что оно не имеют корней.
4. Является ли число х корнем уравнения (слайд 4)
�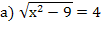 � , х = ± 5 да
� , х = ± 5 да
�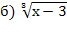 � = �
� = �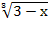 � , х =3 да
� , х =3 да
в) �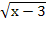 � =�
� =�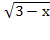 �, х = 5 нет
�, х = 5 нет
5. Какие методы решения иррациональных уравнений вы знаете?
Метод возведения в степень равную показателю корня. Метод выделения квадрата двучлена Метод введения новой переменной Метод разложения на множители. Метод перехода к уравнению с модулем Мы изучили основные методы решения иррациональных уравнений. Методы решения иррациональных уравнений, как правило, основаны на возможности перехода от иррационального уравнения к рациональному уравнению.
6. Какие уравнения называются равносильными?
Два уравнения равносильны на множестве, если они имеют одни и те же корни из этого множества или не имеют корней на этом множестве.
О чем необходимо помнить при решении иррациональных уравнений известными нам методами?
При возведении частей уравнения в четную степень получаем уравнение – следствие, решение которого приводит порой к появлению посторонних корней. Поэтому при использовании данного метода следует проверить все найденные корни подстановкой в исходное уравнение. Иногда удобнее решать иррациональные уравнения, определив область допустимых значений неизвестного и используя равносильные переходы. Возводя обе части уравнения в нечетную степень, переходим к равносильному уравнению.
При возведении частей уравнения в нечетную степень - проверка не нужна.
При разложении на множители надо помнить, что произведение равно нулю, когда хотя бы один из множителей равен нулю, а другой при этом не теряет смысла.
Используя, при решении иррациональных уравнений, метод выделения квадрата двучлена, мы получаем уравнение, содержащее модуль. (Оценка на графике самоанализа)
IV. Работа в парах. Работа по карточкам. Определить соответствие.
Соедините линиями, соответствующие части математических высказываний (слайд 5)
| При возведении обеих уравнений в четную степень |     
| Получается уравнение равносильное данному. |
| При возведении обеих уравнений в нечетную степень | Получается уравнение – следствие данного. |
| Уравнение вида
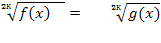
| 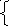 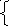 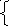 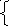 Равносильно системе вида Равносильно системе вида f(х) =�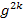 �(x) �(x) g(x) »0 |
| Уравнение вида
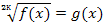 | Равносильно уравнению f(x)=g(x) |
| Уравнение вида
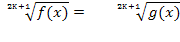
| 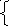  Равносильно системам Равносильно системам f(x)=g(x) f(x)=g(x) g(x) »0 или f (x) »0 |
После выполнения задания, выполняем самопроверку: учащиеся по очереди комментируют свои ответы, на экране с помощью анимации появляются правильные ответы.
Однако при решении иррациональных уравнений не всегда следует сразу приступать к «слепому» применению алгоритма решения.
V. Метод анализа уравнения.
Среди иррациональных уравнений встречаются такие, которые не решаются с помощью методов, которые мы изучили. В подобных случаях иногда может оказаться полезным анализ области определения функций, входящих в уравнение, а также использование свойства корней степени n.
Отметим следующие свойства корней, которыми мы будем постоянно пользоваться при решении уравнений этим методом:
Все корни четной степени являются арифметическими, т.е.,
если подкоренное выражение отрицательное, то корень лишен смысла:
если подкоренное выражение равно нулю, то корень также равен нулю
если подкоренное выражение положительно, то значение корня положительно.
Все корни нечетной степени определены при любом значении подкоренного выражения.
Функция у =� � и у =�
� и у =� � являются возрастающими на своей области определения.
� являются возрастающими на своей области определения.
В ряде случаев можно установить, что уравнение не имеет решения.� �
�
� � +�
� +� � = �
� = � �
�
� � = -�
� = -� �
�
арифметический корень не может быть отрицательным числом, поэтому уравнение не имеет решения.
б)� � +�
� +� � =4 �� Уравнение не имеет решений.
� =4 �� Уравнение не имеет решений.
в)� � = 1 �
� = 1 � ��
�� �
�
Уравнение не имеет решений.
�
 � -�
� -� � =2
� =2
4-х ≥ 0� � х ≤ 4, х ≥ 6 уравнение не имеет решений. �
� х ≤ 4, х ≥ 6 уравнение не имеет решений. � �≥ 0
�≥ 0
Использование монотонности и ограниченности функции.
Использование монотонности функций, входящих в уравнение, порой значительно упрощает техническую часть решения. Сформулируем два свойства монотонных функций и теорему о корне.
1. Сумма возрастающей (убывающей) функции – функция возрастающая (убывающая) на их общей области определения.
2. Разность возрастающей и убывающей функции – функция возрастающая (соответственно убывающей и возрастающей) функций – функция возрастающая (убывающая) на их общей области определения.
3. Теорема о корне. Пусть у = f(x) – монотонная на некотором промежутке функция. Тогда при любом значении а, уравнение f(x) = а имеет на этом промежутке не более одного корня.
Примеры.
� � -�
� -� � =2
� =2
Данное уравнение можно решать стандартным способом, но задача допускает иное решение. Левая часть уравнения – возрастающая в своей области определения функция. Разность между возрастающим и убывающим значением радикала возрастает. Следовательно, уравнение имеет не более одного корня. Его легко найти подбором: это х=1
VI. Этап всесторонней проверки знаний.
Классификация логарифмических уравнений по методам.
Учащимся предлагается провести классификацию иррациональных уравнений по методам решения и заполнить средний столбец (см. таблицу). Таблица изображена на слайде 4 и на карточках у каждого ученика на парте. .(слайд 6)
| № | Уравнения | № метода | № | Методы |
| 1 | 
| 5 | 1 | Метод разложения на множители. |
| 2 | � � +� � +� � =8 � =8 | 3 | 2 | Метод введения новой переменной |
| 3 | � � +� � +� � =2 � =2 | 5 | 3 | Метод анализа уравнения |
| 4 | 2� �+3х +� �+3х +� � =33 � =33
| 2 | 4 | Метод выделения квадрата двучлена. |
| 5 | � � –� � –� � =1 � =1
| 2 | 5 | Метод возведения в степень обеих частей уравнения
|
| 6 | (2х-15)� � =� � =� � � | 1 |
|
|
| 7 | � �+� �+� �=11 �=11
| 4 |
|
|
После того, как учащиеся заполнили средний столбец на местах, заполняем его в таблице на доске, проверяем правильность заполнения на местах.
2) Следующая работа на этом этапе - решение уравнений из таблицы.
Четыре ученика решают уравнение №4, №5, №6 ,№7, остальные на местах решают любой из этих номеров, с последующей проверкой и оценкой. Оценка отмечается на графике самоанализа.
� � Ответ:3
� Ответ:3
� � +�
� +� � =8 Ответ: 10
� =8 Ответ: 10
� � +�
� +� � =2 Ответ: -15, 13
� =2 Ответ: -15, 13
2� �+3х +�
�+3х +� � =33 Ответ: -4,5; 3
� =33 Ответ: -4,5; 3
� � –�
� –� � =1 Ответ: 2,5
� =1 Ответ: 2,5
6) (2х-15)� � =�
� =� � Ответ: 9
� Ответ: 9
7) � �+�
�+� � =11 Ответ: -6; 5
� =11 Ответ: -6; 5
VII Этап решения проверочной работы
I вариант
Решить уравнения:
� � =2
� =2
в)�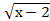 � +8 = х
� +8 = х
c) � � = 2�
� = 2� �
�
2.вариант.
Решить уравнение:
� � =5
� =5
в)� � +2=х
� +2=х
c) � � + �
� + � � = 4
� = 4
VIII Этап подведения итогов. Рефлексия
Подводим итог урока.
По итогам этапов урока, учащиеся выставляют оценки на графике самоанализа. В конце урока выставляют итоговую оценку.
Кто оценил себя на «5»?на «4»? Почему вы уверены, что оценили себя верно?
Чем удовлетворены на уроке? Чем неудовлетворены?
Что получилось? Что не получилось?
� �. Этап домашнего задания.
�. Этап домашнего задания.
Домашнее задание предусматривает уровневую дифференциацию.
1-й уровень – задание репродуктивного характера – решить уравнения из таблицы №1 и №2
2-й уровень – задание поискового плана:
Подобрать уравнения, решаемые методом 1-4.
3-й уровень: При каких значениях параметра a имеются решения уравнения
Найти эти решения.
Приложение №1
Анализ проверочной работы
11 «Б» класс. 27.02.13 г. Тема «Решение иррациональных уравнений» (VII этап)
| № |
Фамилия, имя |
|
|
|
Оценка |
|
|
| 1 уравнение | 2 уравнение | 3 уравнение |
|
| 1 | Бисенбаева Г | + | + | + | 5 |
| 2 | Борисова Д | + | + | + | 5 |
| 3 | Бухаров Е | + | - | + | 3 |
| 4 | Власов Д | + | + | + | 4 |
| 5 | Гаврилов М | + | - | + | 3 |
| 6 | Гимадова М | + | + | + | 5 |
| 7 | Джанбырбаев А | + | + | + | 4 |
| 8 | Есиркепова Г | + | + | + | 4 |
| 9 | Жукова Л | + | + | + | 5 |
| 10 | Жумабеков Д | + | + | - | 4 |
| 11 | ЗвигенцеваЕ | + | + | + | 5 |
| 12 | Калачиков А | - | + | + | 4 |
| 13 | Манапов Д | + | + | + | 4 |
| 14 | Муратбек У | + | + | + | 4 |
| 15 | Наби Н | + | + | + | 5 |
| 16 | Немченко С | + | + | + | 4 |
| 17 | Малышко В | - | + | + | 4 |
| 18 | Семакин А | + | + | + | 5 |
| 19 | Серафимчик М | + | + | + | 4 |
| 20 | Панфилов Д | + | - | + | 3 |
| 21 | Черепанова Т | + | + | + | 4 |
| 22 | Финк Артем | + | - | + | 3 |
Успеваемость – 100% «5» - 7 «4» - 11 «3» - 4
Качество – 82%
Приложение №2.
Карточка для построения графика деятельности учащегося на уроке
Образец построения графика
 Оценка
Оценка
5
4
3
2

 1
1
II III IV VI VII Этапы
 Оценка
Оценка
5
4
3
2

 1
1
II III IV VI VII Этапы
В ыполнил: Наби Н.
ыполнил: Наби Н.
9


 Получите свидетельство
Получите свидетельство Вход
Вход
















 Урок математики на тему "Методы решения иррациональных уравнений" (1.22 MB)
Урок математики на тему "Методы решения иррациональных уравнений" (1.22 MB)
 0
0 919
919 49
49 Нравится
0
Нравится
0


