| "Решение иррациональных, показательных и логарифмических уравнений. Подготовка к ЕНТ" (11-й класс) («Что учиться можно только весело… Чтобы переварить знания, надо поглощать их с аппетитом» французский писатель Анатоль Франс) |
| Цели урока | Показать практическую значимость решение иррациональных, показательных и логарифмических уравнений |
| Задачи урока | Образовательные: повторить, обобщить и систематизировать знания об иррациональных, показательных и логарифмических уравнениях и их решений; сформировать у учащихся умения и навыки по решению уравнений; активизировать познавательную деятельность, раскрыв эффективность и практическую пользу в применении метода подстановки в условиях ограниченного времени при сдаче ЕНТ по математике. Развивающие: развивать умение применять ранее изученное на уроках математики в новой ситуации при решении тестовых задач по математике; обеспечить условия для совершенствования мыслительных умений учащихся: сравнивать, анализировать, обобщать. Воспитательная: содействовать воспитанию интереса к математике. |
| Ожидаемый результат обучения | Учащиеся умеют: - применять зависимости между компонентами арифметических действий, готовых формул, свойств соответствующих функции и т.д. - преобразовывать исходные уравнения для приведения их к уравнениям-следствиям; - находить корни уравнений; - применять основные способы решения уравнений (возведение уравнения в натуральную степень, логарифмирование и потенцирование уравнений, освобождение уравнения от знаменателей, применение нескольких преобразований) - анализировать, комментировать, давать оценку. |
| Основные понятия урока | «уравнения-следствия», иррациональные уравнения, показательные уравнения, логарифмические уравнения возведение уравнения в натуральную степень, логарифмирование и потенцирование уравнений, освобождение уравнения от знаменателей, применение нескольких преобразований. |
| Основная идея урока (ключевая идея) | Умение применить основные способы решения уравнений различных видов |
| Ресурсы | Учебник, компьютер, презентация, карточки с задачами по математике |
| Тип урока | урок проверки, оценки и коррекции знаний, навыков и умений |
| Оборудование | Интерактивная доска |
| Формы работы на уроке | самостоятельная, фронтальная работа, работа в группах. |
| Методический комментарии | данный урок проводится в рамках подготовки к ЕНТ по математике |
| Содержание урока | Деятельность учителя | Деятельность ученика |
| Организационный момент. Психологический настрой. 2 мин | Приветствие, проверка подготовленности к учебному занятию, организация внимания детей. Положительный настрой на работу. Приветствие “Здравствуйте!” Потрите ладошки, предвкушая интересную работу
| Включаются в деловой ритм урока. Настрой на работу. Приветствие “Здравствуйте!” Приветствие “Здравствуйте!” Учащиеся поочередно касаются одноименных пальцев рук своего соседа, начиная с больших пальцев и говорят: . |
| Совместное целеполагание. 5 мин Устный опрос | Чтобы определить тему урока давайте проверим а) теоретические знания; б) практические умения А) Теоретические знания (Учитель читает вопрос, учащийся отвечает, на слайде появляется правильный ответ) Что такое уравнение? (Уравнение – равенство двух алгебраических выражений). Что называется корнем уравнения? (Корень уравнения – такое значение переменной, при котором уравнение обращается в верное числовое равенство). Какие уравнение называются равносильными? (Уравнения называют равносильными, если они имеют одни и те же корни или не имеют корней вообще). Что значит решить уравнение? (Решить уравнение – это значит найти все его корни или доказать, что корней нет).
В) Практические умения Какие из чисел 5, 0 и -3 являются корнями уравнения? | Уравнение | Ответ | | 53х = 35х | 0 | | 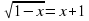
| 0 | | 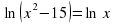
| Ни одного из чисел | Будем на уроке активны, внимательны, будем «поглощать» знания с большим желанием, ведь они скоро вам понадобятся. Определим цели нашего сегодняшнего урока.
|
Читают вопрос, с места отвечаю, на слайде появляется правильный ответ
Записывают дату и тему в тетрадь, определяют цель урока Задача урока: Повторить типы, методы и особенности решения иррациональных, показательных и логарифмических уравнений.
|
| Актуализация опорных знаний. 5 мин
| На уроках математики мы познакомились с решениями иррациональных, показательных и логарифмических уравнений. Сегодня на уроке мы поговорим о том, как можно рационально решить уравнения значительно упростив решение и сократив тем самым его время, увидим эффективность и поймем практическую пользу такого способа решения в условиях ограниченного времени при сдаче ЕНТ. Но прежде чем приступить к решению тестовых задач предложенных на ЕНТ, решим уравнение различных видов. Учащимся раздаются карточки. Решают по вариантам, через 3 минуты собрать. | С/ Р Вариант 1 Решите уравнение 1. 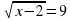 (83) (83) 2. 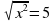 (±5) (±5) 3. 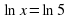 (5) (5) 4. 2х = 7 (log27) 5.  (±3) (±3) 6. 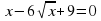 (9) (9) 7. 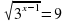 (5) (5) 8. log9 (x-1)2 = 1 (4, -2) 9. 4x – 2x = 0 (0) 10. x logax – log3 2x = 0 (2) | С/ Р Вариант 2 Решите уравнение 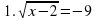 (корней нет) (корней нет)
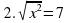 (±7) (±7)
3.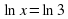 (3) (3) 4. 2х = 9 (log29) 5.  (±3) (±3) 6. 051-х = 16х (-1/3) 7. 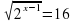 (5) (5) 8. log16 (x-1)2 = 1 (5, -3) 9. 5x – 3x = 0 (0) 10. 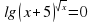 (0) (0) | Время вышло, оцените свою работу по следующим критериям «5» - 10-9 (+), «4» - 8-7 (+), «3» - 5-6 (+),
Обменяйтесь карточками и проведите взаимопроверку. | Решают уравнения и оценивают свои работы Самопроверка, После выполнения задания, проверка работы с помощью интерактивной доски (взаимопроверка)
|
| Работа в группах 3+2 мин | Каждой группе учитель выдает конверт. В этом конверте карточки, на которых задания. Решить более рациональным способом. 1группа Укажите, какому промежутку принадлежит корень уравнения log4(x +12) logx 2 = 1: (-4; -2); 2) (5; 6); 3) (3;5); 4) [-5; -3] 2 группа Укажите, какому промежутку принадлежит корень уравнения  = 243 = 243
[0; 1]; 2) [3; 4]; 3) (-3; -2); 4) (2; 3); 3 группа Решите уравнение 
(-12; 7) 2) (12) 3) (12; 7) 4) (7 ) | Правила работы в группах (повторить) Взаимодействуют друг с другом, сообща выполняют учебную задачу, приводят аргументы, анализируют их значимость. Представлений решений:
Вывод: |
| Физкульминутка(2 мин) | Пальчиковая гимнастика | Ученики выполняют гимнастику |
| 5 мин | Еще один пример: Укажите, какому промежутку принадлежит корень уравнения 4х+1 – 22х = 24 (1; 2); 2) (2; 4); 3) (0; 1); 4) (4; 6) | Традиционный способ решения | Рациональный способ решения | | 22(х+1) – 22х = 24 22х *22 – 2х =24 22х (4 -1) =24 22х = 24:3 22х = 8 22х = 23 2х =3 Х = 1,5 Ответ: (1;2)
| 4х+1 – 22х = 24 42,5 – 23 = 24 32-8=24
| Какое решение вам больше нравится? Почему? | К доске выходят двое равносильных учеников, ребята на местах следят за временем решения каждого из них Выводы учащихся:
|
| Закрепление. Работа в группах. 12 мин | Каждая группа получает задание, решить уравнения двумя способами: традиционным способом и способом подстановки Сделать выводы, какой способ сокращает время решения задачи? Критерий оценок: «5» - 6 выполненных заданий; «4» - 4-5 заданий; «3» -3 задания; «2» - менее 3заданий Задания 1 варианта 1.Укажите промежуток, которому принадлежит корень уравнения Log3(1-x) = 4 А) (62; 64) В) (79; 81) С) (-81; -79) Д) (-12; -10) 2.Сколько корней имеет уравнение 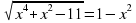 А) 0 В) 1 С) 2 Д) 4 3.Найдите сумму корней уравнения  А) -13 В) -5 С) 5 Д)9 4. Укажите промежуток, которому принадлежит корень уравнения  А) (-4; -2) В) (1; 2) С) (2; 4) Д) (4; 6) 5.Решите уравнение 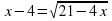 А) 5 В) -1 С) 5; -1 Д) -5 6.Найдите наименьший корень уравнение 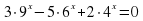 А) -1 В) 0 С) 1 Д) 2 Задания 2 варианта 1.Укажите промежуток, которому принадлежит корень уравнения 4х+1 – 22х = 24 А) (1; 2); В) (2; 4); С) (0; 1); Д) (4; 6) 2. Найдите произведение корней уравнения 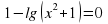 А) -99 В) -9 С) 33 Д) -33 3. Найдите сумму корней уравнения 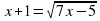 А) -1 В) 1 С) 4 Д) 5 4. Укажите промежуток, которому принадлежит корень уравнения  А)(19; 21) В) (-1; 1) С) (-11; -9) Д) (9; 11) 5. Найдите корень уравнения  А) 0 В) нет корней С) 0; 1 Д) 2 6.Найдите корень уравнения  А) 0 В) -3 С) 0; -3 Д) нет корней Задания 3 варианта 1. Найдите сумму корней уравнения  А) -1 В) 1 С) 4 Д) 5 2. Укажите промежуток, которому принадлежит корень уравнения  А) (-7; -5) В) (-5; -3) С) (2; 4) Д) (5; 7) 3. Укажите промежуток, которому принадлежит корень уравнения 
А) (-4; -2) В) (-2; -1) С) (-1; 0) Д) (1; 2) 4.При каких значениях аргумента значение функции f(x) =3*2x+1 равно96? А) 5 В) таких значений нет С) -7 Д) 4 5.Найдите корень уравнения А) 0.1 В) 2.5*520 С) 0.1 и 2.5*520 Д) нет решений 6.Сколько решений имеет уравнение А) 1 В) 2 С) 3 Д) 4
| Самопроверка (количество выполненных заданий) Взаимопроверка (на экране слайд с ответами |
| Домашняя работа. 2 мин | Дифференцированная домашняя работа: 1. Задачи из сборников по ЕНТ: Подобрать уравнения (иррациональные, показательные и логарифмические) из сборника ЕНТ – 2015 | Записывают задания в дневник. Оценки за урок |
| Итог урока. 3 мин | Мы сегодня повторили применений различных способов решения уравнений. Те вопросы, которые мы сегодня рассмотрели, помогут вам при решении задач по математике на государственных экзаменах и на ЕНТ. Были ли достигнуты цели урока? |
|
| Рефлексия. 2 мин | Ребята, выходя из класса, сделайте для себя вывод об уроке, прикрепив красный кружок к соответствующей фразе.  Урок был полезным и плодотворным для меня. Я получил заслуженную оценку, и понял весь материал Урок был полезным и плодотворным для меня. Я получил заслуженную оценку, и понял весь материал
Урок был интересен и полезен, я принимал активное участие, мне было легко и комфортно.  Пользы от урока я получил мало, я не очень понимаю материал, мне это не интересно и не понятно Пользы от урока я получил мало, я не очень понимаю материал, мне это не интересно и не понятно
Спасибо за плодотворную работу. Всего вам доброго. |
|
| Заключение 1 мин | А закончить наш урок хотелось бы высказыванием академика, математика Алексея Николаевича Крылова «Рано или поздно всякая правильная математическая идея находит применение в том или ином деле». |
|

 Получите свидетельство
Получите свидетельство Вход
Вход



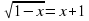
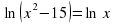
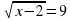 (83)
(83)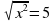 (±5)
(±5)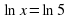 (5)
(5) (±3)
(±3)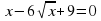 (9)
(9)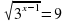 (5)
(5)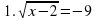 (корней нет)
(корней нет)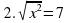 (±7)
(±7)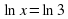 (3)
(3)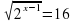 (5)
(5)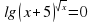 (0)
(0) = 243
= 243
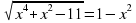


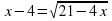
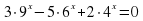
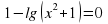
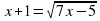











 Конспект урока по математике на тему "Решение иррациональных, показательных и логарифмических уравнений" (46.92 КB)
Конспект урока по математике на тему "Решение иррациональных, показательных и логарифмических уравнений" (46.92 КB)
 0
0 772
772 83
83 Нравится
0
Нравится
0


