Урок математики "Конус"

ПЛАН

Открытого урока по математике

Тема: КОНУС

Подготовила преподаватель математики

Кузьмина Марина Юрьевна

Нижнекамск 2013

Формируемые компетенции

ОК 1. Понимать сущность и социальную значимость своей будущей профессии, проявлять к

ней устойчивый интерес

ОК 2. Организовывать собственную деятельность , исходя из цели и способов её достижения,

определённых руководителем

ОК 3. Анализировать рабочую ситуацию , осуществлять текущий и итоговый контроль , оценку

и коррекцию собственной деятельности , нести ответственность за результаты своей

работы.

ОК 4. Осуществлять поиск информации, необходимой для эффективного выполнения

профессиональных задач

ОК 5. Использовать информационно- коммуникационные технологии в профессиональной

деятельности

ОК 6. Работать в команде, эффективно общаться с коллегами, руководством, клиентами.

Цели урока

Образовательные:

-формирование знаний о конусе, о конусообразных телах в окружающем мире, истории развития представлений о конусе;

- формирование компетенции в сфере самостоятельной познавательной и практической деятельности,

Развивающие :

-развитие умения по нахождению элементов конуса и площади поверхности конуса;

- развитие математически грамотной речи, логического мышления, сознательного восприятия учебного материала; умения структурировать и анализировать полученную информацию;

Воспитательные цели:

- воспитание навыков эстетического оформления записей в тетради и выполнения чертежей, умения работать в парах , прививать интерес к предмету

Тип урока: изучение нового материала

Вид урока :

Материально-техническое оснащение : плакаты, карточки с кроссвордом, карточки-задания для самостоятельной работы.

Ход урока

I. Организационный момент.

Приветствие. Проверка присутствующих на уроке. Проверка готовности обучающихся к уроку.

II. Актуализация опорных знаний.

Тема сегодняшнего урока важна , она непосредственно связанна с нашей жизнью .

-Мы продолжаем с вами изучать тела вращения и сегодня на уроке вы узнаете о ещё одном теле вращения , где оно встречается. И прежде , давайте кое-что вспомним . Разгадаем кроссворд.

- Какое ключевое слово у вас получилось : Сосновая шишка.

- Как вы думаете , какое отношение к нашему уроку имеет сосновая шишка? ( ответы обучающихся)

Историческая справка. Сообщение обучающегося.

Конус в переводе с греческого “konos” означает “сосновая шишка”. С конусом люди знакомы с глубокой древности.

В 1906 году была обнаружена книга Архимеда (287-212 гг. до н.э.) “О методе”, в ней рассказывается о методе решения задачи об объеме общей части пересекающихся цилиндров. Архимед приписывает честь открытия этого принципа Демокриту (470-380 гг. до н.э.) – древнегреческому философу-материалисту. С помощью этого принципа Демокрит получил формулу для вычисления объема пирамиды и конуса.

Много сделала для геометрии школа Платона (428-348 гг. до н.э) среди прочего в этой школе занимались а) исследованием свойств конуса; б) изучением конических сечений.

Большой трактат о конических сечениях был написан Аполлонием Пергским (260-170 гг. до н.э.) – учеником Евклида (III в. до н.э.).

Итак , следующее тело вращение, которое мы будем изучать –это конус.

Запишите тему урока –«Конус»

Сегодня мы рассмотрим , что такое конус, изучим элементы конуса, рассмотрим способ получения конуса, виды конусов и порешаем задачи.

III. Изучение нового материала.

1. Понятие конуса.

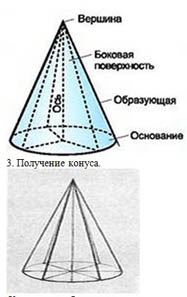
Рассмотрим окружность L с центром О и прямую ОР. Перпендикулярную к плоскости ά этой окружности. Через точку Р и каждую точку окружности проведём прямую. Поверхность, образованная этими прямыми , называется конической поверхностью, а сами прямые –образующими конической поверхности. Точка Р называется вершиной, а прямая ОР-осью конической поверхности.

Определение: Тело, ограниченное конической поверхностью и кругом с границей L, называется конусом.

2.Элементы конуса.

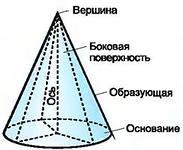
3. Получение конуса .

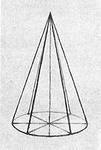
Конус может быть получен вращением прямоугольного треугольника вокруг одного из его катетов

4. Сечение конуса.

Рассмотрим сечение конуса различными плоскостями.

Если секущая плоскость проходит через ось конуса, то сечением будет равнобедренный треугольник, основание которого-диаметр основания конуса, а боковые стороны- образующие конуса. Это сечение называют осевым.

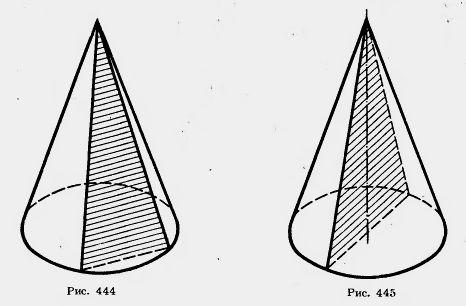
Если секущая плоскость перпендикулярна к оси Ор конуса, то сечение представляет собой круг с центром О1, расположенным на оси конуса.

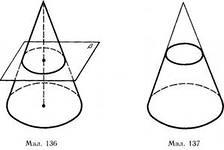
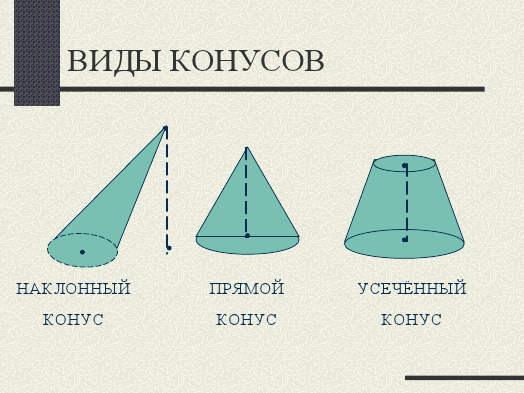
5 Виды конусов.

6. Конусы в нашей жизни. Сообщение обучающегося.

IV. Закрепление изученного материала.

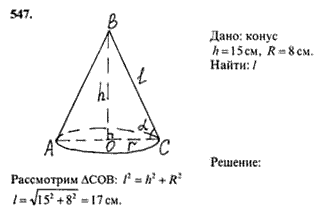
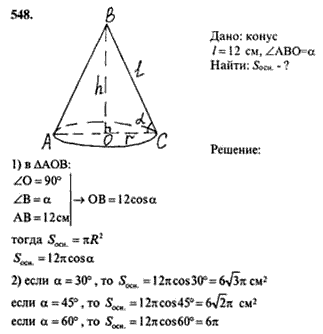
1. Решение задач из учебника

№ 547, №548.

2. Самостоятельная работа

1. какое из изображённых тел является конусом?

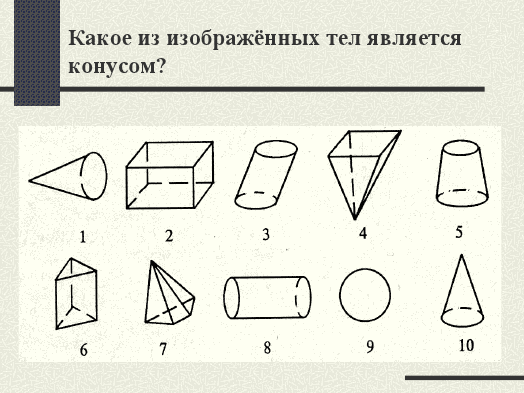
2. Заполните пропуски.

а). Тело , полученное вращением прямоугольного треугольника вокруг одного из катетов, это-..

б). Основанием конуса является - ….

в)Отрезок, заключённый между вершиной и основанием конуса называется…

3. Радиус основания конуса равен 3 см, а высота 4 см. Найти образующую и площадь осевого сечения

V. Подведение итогов. Д/З

Итак, мы с вами познакомились ещё с одним телом вращения -конусом . Вопрос о конусе важен, и на следующем уроке мы с вами продолжим изучение конуса.

Д.З. Повторить всё что узнали о конусе. Сделать свою модель конуса из бумаги , для работы на следующем уроке.

Применение конуса

Знания о конусе широко применяются в жизни - в быту, на производстве, в науке. Например, в быту мы часто используем вёдра, имеющие форму усечённого конуса, служащие нам ёмкостью для различных жидкостей и сыпучих веществ. Наши растения, благоприятно развиваются в цветочных горшках. А эти предметы чаще всего имеют форму либо прямого кругового конуса, либо форму усечённого конуса. 

Для переливания жидкостей из более крупной посуды, в более мелкую мы используем воронку. Если присмотреться к её форме, мы заметим, что она похожа на усечённый конус.

Идя по улице, мы можем увидеть человека с интересным приспособлением в руках. Это рупор. Он служит для усиления звука, то есть он является громкоговорителем. В жизни мы нередко встречаемся с конусами. Ночная лампа в виде конуса. Лампа с абажуром отбрасывает пучок света в виде конуса.

Спортивный инвентарь или ограждения тоже принимают форму конуса.

Очень часто мы встречаем конус в элементах архитектуры. Ярким примером этого наблюдения является конус, который лежит в основании крыш домов. некоторые жилища имеют форму конуса.

В природе мы тоже можем встретить конус. Например, в песчаной пустыне Сахаре, где сами холмы представляют собой конус.
В биологии есть понятие “конус нарастания. Это верхушка побега и корня растений, состоящая из клеток образовательной ткани.

“Конусами” называется семейство морских моллюсков подкласса переднежаберных.

Любимое лакомство детей мороженное и конфеты- тоже имеют форму конуса.

По статистике на Земле ежегодно гибнет от разрядов молний 6 человек на 1 000 000 жителей (чаще в южных странах). Этого бы не случалось, если бы везде были громоотводы, так как образуется конус безопасности. Чем выше громоотвод, тем больше объем такого конуса. некоторые люди пытаются спрятаться от разрядов под деревом, но древо не проводник, на нем заряды накапливаются и дерево может быть источником напряжения.

Конические детали имеются во многих машинах и механизмах. В автомобилях– конические шестерни : носовая часть самолетов и ракет имеет коническую форму.

В физике встречается понятие “телесный угол. Это конусообразный угол, вырезанный в шаре. Свет от киноаппарата, прожектора распространяется в виде конуса.

Ну и конечно же у нас студентов всегда при себе ручка. Если посмотреть внимательно, конец ручки тоже имеет коническую форму.

.

Конус в переводе с греческого “konos” означает “сосновая шишка”. С конусом люди знакомы с глубокой древности.

В 1906 году была обнаружена книга Архимеда (287-212 гг. до н.э.) “О методе”, в ней рассказывается о методе решения задачи об объеме общей части пересекающихся цилиндров. Архимед приписывает честь открытия этого принципа Демокриту (470-380 гг. до н.э.) – древнегреческому философу-материалисту. С помощью этого принципа Демокрит получил формулу для вычисления объема пирамиды и конуса.

Много сделала для геометрии школа Платона (428-348 гг. до н.э) среди прочего в этой школе занимались а) исследованием свойств конуса; б) изучением конических сечений.

Большой трактат о конических сечениях был написан Аполлонием Пергским

(260–170 гг. до н. э.) – учеником Евклида (III в. до н. э.), который создал

великий труд из 15 книг под названием «Начала». Эти книги издаются и по сей

день, а в школах Англии по ним учатся до сих пор.

1. какое из изображённых тел является конусом?

2. Заполните пропуски.

а). Тело , полученное вращением прямоугольного треугольника вокруг одного из катетов, это-..

б). Основанием конуса является - ….

в)Отрезок, заключённый между вершиной и основанием конуса называется…

3. Радиус основания конуса равен 3 см, а высота 4 см. Найти образующую и площадь осевого сечения

1. какое из изображённых тел является конусом?

2. Заполните пропуски.

а). Тело , полученное вращением прямоугольного треугольника вокруг одного из катетов, это-..

б). Основанием конуса является - ….

в)Отрезок, заключённый между вершиной и основанием конуса называется…

3. Радиус основания конуса равен 3 см, а образующая 5 см. Найти высоту и площадь осевого сечения

1. Прямая , соединяющая центры двух оснований цилиндра.

2. Отрезки, заключённые между основаниями цилиндра.

3. Отрезок, соединяющий центр основания О с точкой на окружности основания

4. Тело, полученное вращением прямоугольника вокруг одной из его сторон.

5. Длина образующей.

6. 2 круга цилиндра с границами L и L 1.

7. Фигура, полученная вращением полуокружности вокруг её диаметра

8.При вращение этой фигуры получается цилиндр.

9. Тело, полученное вращением полукруга вокруг его диаметра.

10 Известный древне-греческий учёный

11. Какая фигура лежит в основании цилиндра

12. Что не имеет ни начала ни конца

1. Прямая , соединяющая центры двух оснований цилиндра.

2. Отрезки, заключённые между основаниями цилиндра.

3. Отрезок, соединяющий центр основания О с точкой на окружности основания

4. Тело, полученное вращением прямоугольника вокруг одной из его сторон.

5. Длина образующей.

6. 2 круга цилиндра с границами L и L 1.

7. Фигура, полученная вращением полуокружности вокруг её диаметра

8.При вращение этой фигуры получается цилиндр.

9. Тело, полученное вращением полукруга вокруг его диаметра.

10 Известный древне-греческий учёный

11. Какая фигура лежит в основании цилиндра

12. Что не имеет ни начала ни конца

12