Цели:
Образовательные: познакомить учащихся с решениями некоторых типов иррациональных уравнений; способствовать развитию навыка решения иррациональных уравнений., научить учащихся решать данные уравнения.
Развивающие: развитие активности учащихся, формирование учебно – познавательных действий при решении уравнений.
Воспитательные: способствовать формированию трудовых навыков и воспитанию аккуратности.
Тип: урок типовых задач
Форма урока: практическое занятие
Оборудование: проектор, слайды для сопровождения урока, карточки
Ход у рока
I. - Здравствуйте, дети! Садитесь. Проверим нашу готовность к уроку (проверка отсутствующих).
II. Проверка домашнего задания.
- Сегодня мы проведем урок практического характера. Цель нашей работы научиться упрощать, решать некоторых типов иррациональных уравнений. Но прежде чем решать уравнения давайте с вами сделаем небольшую разминку «Устная работа».
II. Устная работа
1) Какие из следующих уравнений являются иррациональными:
2) Является ли число х0 корнем уравнения:
3) Найти область определения функции:
III. Решение иррациональных уравнений (подготовка учащихся к активному усвоению знаний)
Рассмотрим решение некоторых типов иррациональных уравнений.
1. Уравнения, в которых одно или несколько подкоренных выражений точные квадраты.
2. Уравнения, содержащие несколько квадратных радикалов.
3. Уравнения, содержащие корни третьей степени.
4. Иррациональные уравнения, решаемые способом замены.
IV. Основная часть
Обобщающее и системное изучение ( работа с учебником №132,133,134нечетные)
V. Выполнение заданий в парах индивидуально.
VI. Итоги. Рефлексия
VII. Домашнее задание №132-134(2.4).
Весь материал – смотрите документ.

 Получите свидетельство
Получите свидетельство Вход
Вход


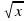
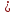 2; б)х
2; б)х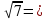 11+х; в)у+
11+х; в)у+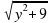
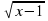
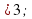 д)
д)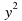 -3у
-3у 4 Ответы: а,в,г
4 Ответы: а,в,г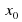 корнем уравнения:
корнем уравнения: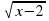
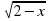 ,
, 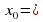 4; б)
4; б)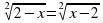 ,
, 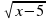
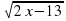 ,
, 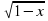
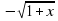 ,
, 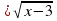 ; б)у
; б)у








 Урок математики "Иррациональные уравнения" (23.91 КB)
Урок математики "Иррациональные уравнения" (23.91 КB)
 0
0 498
498 12
12 Нравится
0
Нравится
0







