На первом этапе мы рассмотрим, что из себя представляет иррациональные уравнения. На втором этапе урока мы попробуем решить ряд иррациональных уравнений. Затем рассмотрим и решим задачу на иррациональные уравнения на материале краеведения.
Тип консультации: ознакомление с новым материалом и первичное закрепление.
Цель: ввести понятие иррациональных уравнений и показать способы их решений.
Задачи:
Предметные – сформировать у учащихся умение решать иррациональные уравнения, отработать навыки решения иррациональных уравнений различными способами
Регулятивные - определять и формулировать цель деятельности; учиться планировать учебную деятельность на ГК; работать по плану, сверять свои действия с целью; соотносить результат своей деятельности с целью и оценивать его; учиться вырабатывать критерии оценки и определять степень успешности выполнения своей работы, исходя из имеющихся критериев.
Коммуникативные – доносить свою позицию до других, владея приёмами монологической и диалогической речи; оформлять свои мысли в устной и письменной речи с учетом учебной речевой ситуации; высказывать свою точку зрения и пытаться её обосновать, приводя аргументы, задавать уточняющие вопросы.
Познавательные – ориентироваться в своей системе знаний и осознавать необходимость нового знания.
Личностные - воспитывать самостоятельность, находчивость, стремление к самосовершенствованию
Материалы разработаны применительно к учебнику «Алгебра и начала анализа, 10 - 11» под редакцией А. Н. Колмогорова.
План групповой консультации
- Проверка домашнего задания, повторение пройденного материала
- Объяснение нового материала
- Закрепление изученного
- Подведение итогов
- Домашнее задание
- Самостоятельная работа.

Ход групповой консультации:
I. Проверка домашнего задания (задание написано на боковой доске)
1) Вычислить
2) Примените формулы сокращенного умножения
Дополнительный вопрос: какие еще виды уравнений вы знаете?
4) Найдите область определения функции:
Дополнительный вопрос: Из заданного промежутка найдите наименьшее целое число
Дополнительный вопрос: Как называются такие уравнения?
II. Объяснение нового материала
Определение. Уравнение, в которых под знаком корня содержится переменная, называют иррациональными
Решить уравнение: (записано на боковой доске) Решается с объяснением учителя
Учащиеся записывают уравнение в тетрадь с комментариями учителя
III. Закрепление изученного
а) Из истории знака квадратного корня
Знак квадратного корня знаком всем. Его используют школьники и студенты, преподаватели по математике, доктора наук и академики. Однако не все знают, что современная форма появилась не сразу. Эволюция знака радикала длилась почти пять веков, начиная с в далекого XIII в. , когда итальянские и некоторые европейские математики впервые называли квадратный корень латинским словом Radix (корень) или сокращенно R.
Современный знак корня произошел от обозначения, примяемого немецкими математиками XV - XVI вв. , называвшие алгебру — наукой «Косс», а математиков - алгебраистов «коссистами». (Математики XII - XV вв. писали все свои труды исключительно на латинском языке. Они называли неизвестное — res (вещь). Итальянские математики перевели словоres как cosa. Последний термин заимствовали немцы, от которых и появилось коссисты и косс. )
В XV в. некоторые немецкие коссисты для обозначения квадратного корня пользовались точкой перед выражением или числом. В скорописи эти точки заменялись черточками.
Скорее всего, в последствии от таких обозначений как раз и образовался знак ü, близкий по записи к знакомому школьникам современному знаку, но без верхней черты. Впервые этот знак был замечен в немецкой алгебре «Красивый и быстрый счет при помощи искусных правил алгебры»
Автором этого труда был преподаватель математики из Вены, уроженец Чехии Криштоф Рудольф. Книга пользовалась большим успехом и постоянно переиздавалась на протяжении всего XVI в. и после аж до 1615г. Знаком корня, предложенного Криштофом пользовались А. Жирар, С. Стевин (он писал показатель корня справа от знака радикала в кружке: V (2) или V (3).
В 1626г. нидерландский математик А. Жирар и видоизменил знак корня Рудольфа и ввел совсем близкое к современному обозначение.
И только в 1637 году Рене Декарт соединил горизонтальную черту с галочкой, применив новое обозначение в своей книге «геометрия».

 Получите свидетельство
Получите свидетельство Вход
Вход






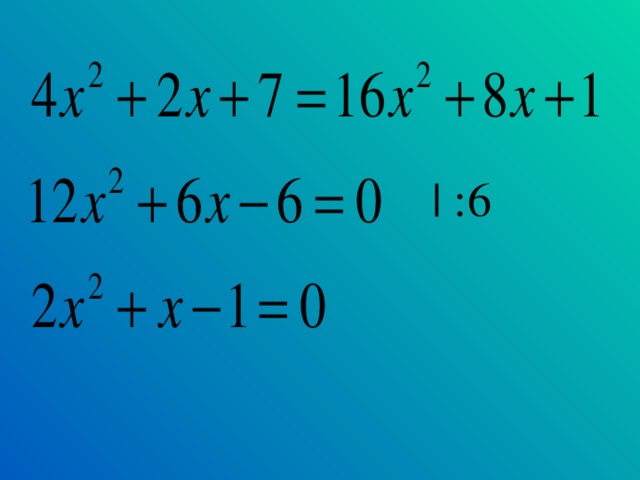
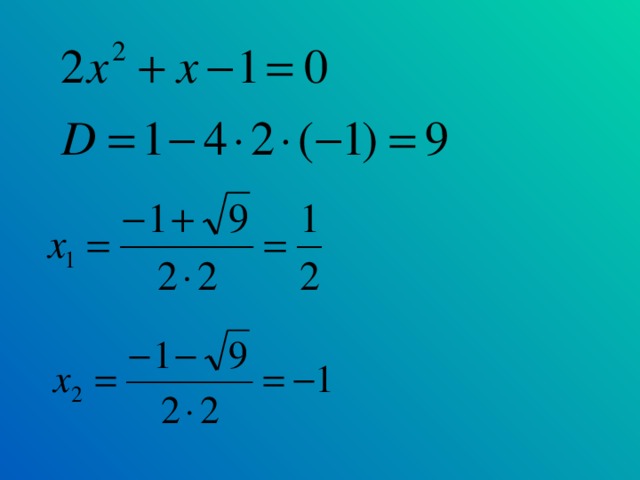
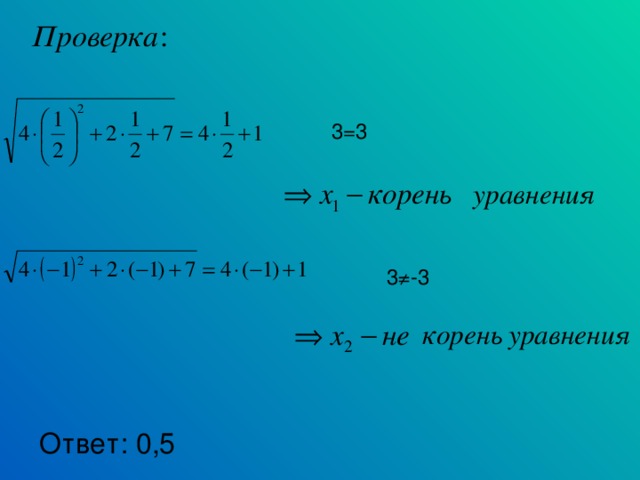

















 Презентация по математике "Иррациональные уравнения" (0.56 MB)
Презентация по математике "Иррациональные уравнения" (0.56 MB)
 0
0 474
474 47
47 Нравится
0
Нравится
0


