Цели урока:
Обучающая – обобщить знания о системах счисления; познакомиться с общим алгоритмом перевода чисел из одной системы счисления в другую.
Развивающая – развивать умение качественно оценивать поставленную задачу для правильного выбора способа решения задачи; развивать самостоятельность; логическое мышления учащихся.
Воспитательная – формировать интерес к предмету, навыки контроля и самоконтроля; чувство ответственности, деловые качества учащихся.
Оборудование: доска, маркер, карточки - памятки, справочный материал.
Тип урока: комбинированный: объяснение нового материала с выполнением практической работы.
Ход урока
I. Организационный момент.
II. Актуализация знаний.
Ребята на прошлом уроке мы с вами вспомнили, что такое система счисления? Давайте сейчас повторим основные моменты:
дайте определение понятия система счисления?
назовите основные системы счисления?
в чем отличие позиционной от непозиционной системы счисления?
определите основные понятия систем счисления: традиционные и нетрадиционные системы; цифра, алфавит системы, основание системы?
почему развернутую форму записи числа называют разложением по базису?
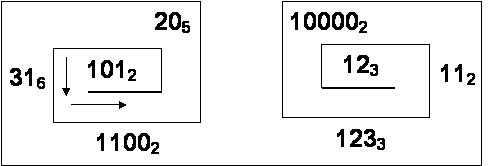
А сейчас решим простое задание: Переведите числа, записанные в различных системах счисления, в десятичную систему счисления; затем полученные после вычисления числа замените буквами русского алфавита, которые имеют соответствующие порядковые номера; запишите полученное слово.
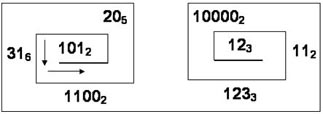
(Ответ: ДИСКОВОД)
Следующая задача, «В саду росло 63q фруктовых деревьев, из них 30q яблони, 21q груши, 5q сливы, 4q вишни. В какой системе счисления ведется счет, и сколько было деревьев?»
В ходе решений, ученики приходят к выводу, что в дано случае семеричная система счисления.
Решение:
63q = 30q + 21q + 5q + 4q
Составим уравнение, согласно правилам записи чисел в позиционных системах счисления
6q + 3 = 3q + 2q + 1 + 5 + 4
q = 7
всего деревьев – 6 * 7 + 3 = 45
яблонь – 3 * 7 = 21
груши – 2 *7 + 1 = 15
слив – 5
вишен – 4
Ответ: Система счисления – семеричная, яблонь – 21, груш – 15, слив – 5, вишен – 4, всего – 45.
III. Изучение нового материала.
Существуют различные системы счисления 2, 3, 4, 5, 6, 7, и т. д. И для все систем счисления существует один алгоритм для перевода из десятичной в n - ую систему счисления и обратно. Рассмотри это на примерах.
Пример 1.
Перевести число 5810 в троичную систему счисления.
Ответ: 5810=20113
Если мы вспомним перевод из десятичной системы счисления в двоичную систему счисления, то мы также десятичное число делили на основание системы, на двойку, если нужно перевести число в троичную систему счисления, то мы делим на три и т. д. Сформулируем общее правило:
Перевод чисел из десятичной системы счисления в другую.
Правило перевода целых чисел из десятичной системы счисления в систему с основанием q:
Последовательно выполнять деление исходного числа и получаемых частных на q до тех пор, пока не получим частное, меньшее делителя.
Полученные при таком делении остатки – цифры числа в системе счисления q – записать в обратном порядке (снизу вверх).
Решить самостоятельно:
Перевести десятичное число 315 в восьмеричную систему счисления и в шестнадцатеричную.
Перевести десятичное число 542 в пятеричную систему счисления и в семеричную.
Теперь рассмотрим перевод десятичной дроби в систему счисления с основанием p.
Весь материал – смотрите документ.

 Получите свидетельство
Получите свидетельство Вход
Вход



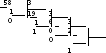


 Решение:
Решение: 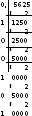









 Урок информатики на тему "Перевод чисел из одной системы счисления в другую" (30.83 КB)
Урок информатики на тему "Перевод чисел из одной системы счисления в другую" (30.83 КB)
 0
0 1838
1838 304
304 Нравится
0
Нравится
0


