20.11.2018. математика Урок № 53.
Преподаватель Рачкова Н. В.
Тема: Решение задач по теме «Метод координат».
Форма урока: Урок практического закрепления знаний по теме «Метод координат» (урок – игра).
Цели:
Обучающая: обобщение и систематизация знаний по теме.
Развивающие: способствовать развитию мышления, познавательной и творческой активности;
развивать умение работать с учебной информацией; навыки самостоятельной работы и работы в группах; умения выполнять задания в отведённое на него время; интерес к предмету.
Воспитательные: учить доводить до конца начатую работу; оценивать свой труд и труд своих товарищей; воспитывать чувство ответственности перед коллективом.
Ожидаемый результат: подтверждение имеющихся у обучающихся базовых знаний по теме;
выявление группы обучающихся, проявляющих интерес к предмету.
Оборудование: таблицы с заданиями; раздаточный материал; учебно - письменные принадлежности.
Организационный момент.
Построение. Рапорт. Перекличка.
Рассадка по командам.
Сообщение темы, задач и целей.
Разминка.
(капитаны команд отвечают на вопросы и получают бонусы для команды).
А.
Вектор это - … (направленный отрезок).
Сколько векторов, равных данному, можно отложить от заданной точки? (один)
В каком случае несколько векторов можно обозначить одинаково? (если векторы равны)
Какой вектор коллинеарен любому вектору? (нулевой вектор)
Как называются два коллинеарных вектора, направленных в одну сторону? (сонаправленные)
На каких сторонах трапеции можно обозначить противоположно направленные векторы? (на её основаниях)
Чем отличаются противоположные векторы от противоположно направленных векторов? (противоположные векторы равны по длине)
Что такое модуль вектора? (длина вектора)
Может ли при сложении двух противоположно направленных векторов получиться нулевой вектор?
Единичные векторы _ это векторы … (координатные векторы
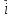 и
и 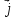 )
)Если координаты двух векторов пропорциональны, то эти векторы … (коллинеарны)
Б.
Установить соответствие между левым и правым столбцами (работа в командах).
|
Дано: А(х1; у1), В(х2; у2) | |
| А координаты вектора Б координаты середины отрезка АВ… В длина отрезка АВ … |
|
А – 2; Б – 1; В – 3 (213)
Решение задач.
На координатной плоскости даны точки: А, В, С, D.
А) Сколько различных векторов (с началом и концом в этих точках) может получиться? (12).
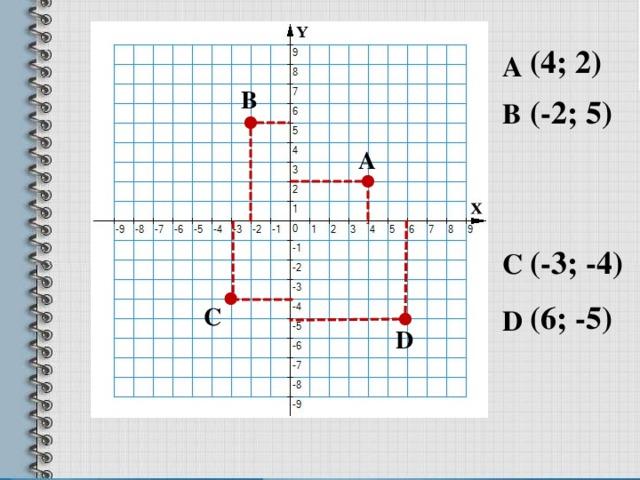
Б) Найдите длину меньшего вектора. (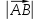 =
= 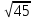 )
)
В) Найдите координаты вектора 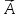 D ( 2; -7).
D ( 2; -7).
2. Р(3; -6) – центр окружности, радиус которой равен модулю ординаты этой точки. Постройте эту окружность.
А. Составьте уравнение окружности. (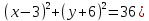
Б. Сколько общих точек имеет окружность с осью Ох? (1)
В. . Сколько общих точек имеет окружность с осью Оу? (2)
Конкурс «Что прячет осень?»
На доске рисунки грибов, на каждом из которых написан номер от 1 до 8. На обратной стороне рисунка – задание. Выполнив задание, игроки выбирают осенний листок с ответом. На обратной стороне каждого листка написано по одной букве. Выполнив правильно все задания, игроки смогут составить слово «листопад».
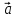
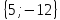 и
и 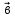
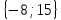 . Найдите координаты вектора
. Найдите координаты вектора 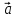 +
+ 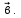 (-3; 3)
(-3; 3)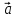
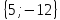 и
и 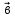
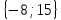 . Найдите координаты вектора
. Найдите координаты вектора 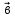 -
- 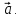 (-13; 27)
(-13; 27)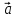
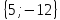 и
и 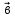
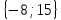 . Найдите координаты вектора -8
. Найдите координаты вектора -8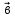 (64; -120)
(64; -120)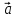
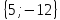 и
и 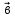
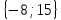 . Найдите координаты вектора
. Найдите координаты вектора (1,25; -3)
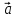
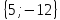 и
и 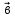
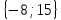 . Найдите модуль вектора
. Найдите модуль вектора 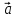 (13)
(13)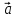
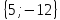 и
и 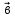
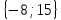 . Найдите 2
. Найдите 2(9)
Каковы координаты вектора
= 1,2
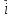 - 0,5
- 0,5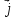 ? (1,2; -0,5)
? (1,2; -0,5)= 1,2
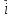 - 0,5
- 0,5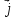 . Найдите
. Найдите . (1,3)
Дополнительная задача.
Определить вид треугольника АВС, если его вершины заданы координатами: А(-7; 2), В(-3; 9), С(1; 2).
Найдите высоту, поведённую из вершины В и площадь треугольника.
(остроугольный, равнобедренный, высота – 7, площадь - 28). Ответы на дубовых листочках.
Итог урока.
Оцените свои знания.
Оцените свою работу.
Подсчёт бонусов по командам. Определение победителя. Выставление отметок.

 Получите свидетельство
Получите свидетельство Вход
Вход


 и
и  )
) …
… ;
; 



 =
=  )
) D ( 2; -7).
D ( 2; -7).

 и
и 
 . Найдите координаты вектора
. Найдите координаты вектора  (-3; 3)
(-3; 3) (-13; 27)
(-13; 27) (1,25; -3)
(1,25; -3) (9)
(9) = 1,2
= 1,2 . (1,3)
. (1,3)

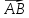 …
…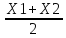 ;
; 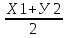
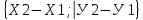
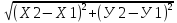









 Урок - игра "Метод координат" (1.86 MB)
Урок - игра "Метод координат" (1.86 MB)
 0
0 517
517 39
39 Нравится
0
Нравится
0


