
Решение уравнений
с модулем.
6 класс.
п.Софиевка
Ярось Ольга Владимировна

Решите уравнение:
4(х - 3) - 18 = 5(х - 5)
4х - 12 - 18 = 5х - 25
4х - 5х = 30 - 25
- х = 5
х = -5

Решите устно рациональным способом:
1
5
(-2,5 + 2,5)
0,7
6,4
-5
1
_
.
.
.
.
_
3
6
0
2
1
17
-5
(-
)
17
3
.
.
.
_
_
17
3
0,3 (-0,6) - (-0,7) (-0,6)
-0,6

Что общего в этих уравнениях?
Чем отличаются эти уравнения?

Разделите уравнения на группы.
По какому принципу можно разделить уравнения?

Повторим определение модуля.
Продолжите фразу:
Модулем положительного числа…
Модулем отрицательного числа…
Модулем нуля…
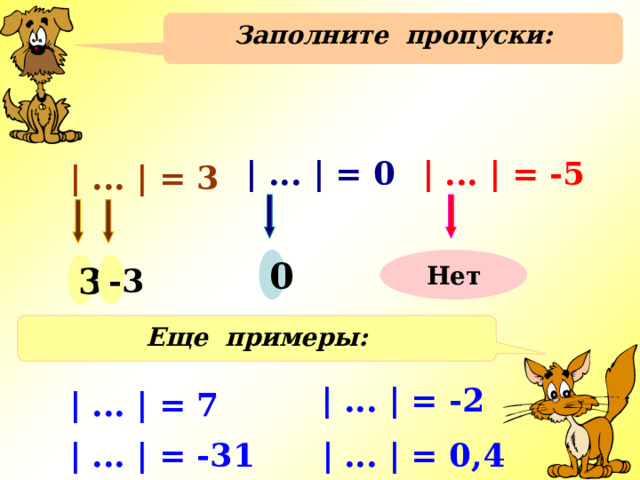
Заполните пропуски:
| ... | = 0
| ... | = -5
| ... | = 3
0
Нет
3
-3
Еще примеры:
| ... | = -2
| ... | = 7
| ... | = 0,4
| ... | = -31
 0 t = a t = -a | x - 6 | = 3 Пример: x - 6 = -3 x - 6 = 3 или x = 3 x = 9 Ответ: 3; 9. " width="640"
0 t = a t = -a | x - 6 | = 3 Пример: x - 6 = -3 x - 6 = 3 или x = 3 x = 9 Ответ: 3; 9. " width="640"
Уравнения с переменной под знаком модуля решаются так:
I
| t | = a;
a 0
t = a
t = -a
| x - 6 | = 3
Пример:
x - 6 = -3
x - 6 = 3
или
x = 3
x = 9
Ответ:
3; 9.

Решите уравнения:
-6; 2
| 2 + x | = 4
-16; 8
| 4 + x | = 12
-1; 0,5
| 4x + 1 | = 3
0,5; 3,5
| 2x - 4 | = 3

Уравнения с переменной под знаком модуля решаются так:
II
| t | = 0
t = 0
| 2 + x | = 0
Пример:
2 + x = 0
x = -2
Ответ:
-2

Решите уравнения:
0,5
| 1 - 2x | = 0
-3,5
| 7 + 2x | = 0
-4
| x + 4 | = 0
0,375
| 8x - 3 | = 0

Уравнения с переменной под знаком модуля решаются так:
III
| t | = a;
a
Нет корней
Пример:
| 6 - x | = -5
Нет корней

Решите уравнения:
Нет корней
| 2x - 5 | = -7
Нет корней
| 0,5 + х| = -5
Нет корней
| 10х - 3 | = -8
Нет корней
| x - 75 | = -3

 Получите свидетельство
Получите свидетельство Вход
Вход











 Уравнения с модулем (165.97 KB)
Уравнения с модулем (165.97 KB)
 0
0 961
961 45
45 Нравится
0
Нравится
0


