Урок алгебры в 9 А классе
Тема: «Решение уравнений с переменной под знаком модуля ».
Тип урока по дидактической цели: изучение и первичное закрепление нового материала.
«Мало знать, надо и применять, мало хотеть, надо и делать».
И. Гете
ЦЕЛИ:
Предметные: 1. Помочь учащимся целостно представить проект изучения новой темы.
2.Организовать деятельность учащихся по изучению и первичному закреплению всех типов уравнений под модулем и схем их решений.
Направленные на развитие ребенка: 1. Актуализировать личностный смысл учащихся к изучению темы.
Помочь учащимся осознать социальную, практическую и личностную значимость учебного материала.
Создать условия для развития у школьников интеллектуальной культуры.
Содействовать развитию у детей умений осуществлять самоконтроль, самооценку и самокоррекцию УД;
Содействовать развитию у детей умений общаться
Форма организации образовательного процесса: лекция.
ХОД УРОКА:
Организационный этап.
Мотивация учебной деятельности, сообщение цели и задач урока, знакомство с планом лекции.
У: существенной характеристикой числа является его абсолютная величина ( или модуль). Это понятие широко применяется в различных разделах школьного курса математики, физики. Вспомним, где применяется модуль числа?
1). Математика.
Модуль – это расстояние от точки О до точки, изображающей это число на координатной прямой (геометрический смысл модуля).
2).Геометрия и физика:




![]() а |а| F |F|
а |а| F |F|
3). Алгебра. Теория приближенных вычислении:
а = 1.5436 b = 1,5. А.П. приближенного значения называется модуль разности точного и приближенного значений. А.п. = | точное значение – приближенное значение|
Кроме того, мы строили графики функций, содержащие модуль числа, решали простейшие уравнения вида | х | = а.
В курсе высшей математики модуль встречается в определении таких основных понятий, как предел функции, ограниченная функция. В углубленном курсе математики мы с вами будем решать серьезные уравнения и неравенства, содержащие переменную под знаком модуля.
Задача нашего урока: рассмотреть основные типы уравнении с модулями и методы их решения. Тема сегодняшней лекции: «Решение уравнений с переменной под знаком модуля ».
Лекция у нас будет активная. Вы не только будете конспектировать, но и отвечать на мои вопросы, формулировать свои вопросы, выполнять задания, искать ошибки и их исправлять. Тема очень серьезная, нужная. Вы сами будете контролировать себя, в листке самоконтроля будете отмечать, что вы хорошо усвоили, а что плохо поняли.
3. Актуализация субъектного опыта учащихся.
Что такое модуль числа?
Устная работа.
1. Найти
|-3,5| | 3,5| | -3,5| - |-3,5| |- | -3,5| |
2. Освободиться от знака модуля:
|√ 2 – 1|; | √ 2 - √ 3|; | - 4| .
Из определения и геометрического смысла модуля вытекают свойства модуля. Расскажет про них ___________________.
Свойства:
1. | а | ≥ 0.
2. | а – b| есть расстояние между точками а и b числовой оси.
3. | -а | = а.
4. |b| = |а| |b|, | а/b| = | а| / |b| ( b ≠ 0)
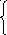 5. | а| = b b≥ 0,
5. | а| = b b≥ 0,
а = b,
а = -b.
6. |а|2 = а2 = | а2|
А теперь проверим, хорошо ли вы понимаете определение.
Работа с сигнальными картами.
Задание: верно ли раскрыт модуль. Если да, то поднимаем зеленую карточку, если нет - красную.
Карточку поднимаете только по моему сигналу. Если ответ верный, ставим «+» в карте самоконтроля напротив номера задания, если нет – знак «-» .
|
| Примеры
| Верно или нет |
| 1.
| |-17 | = 17 | + |
| 2.
| - | -5| = 5 | - |
| 3.
| | - | - | -П | | | = П
| + |
|
4.
|
| √3 - 2 | = √3 - 2 | - |
| 5.
| |-а | = а | - |
| 6.
| |а | = - а | - |
Организация восприятия и осмысления нового материала и первичная проверка материала.
Из определения и свойств модуля вытекают основные методы решения уравнений с модулями. Это:
- «раскрытие модуля по определению;
- использование геометрического смысла модуля;
- использование равносильных преобразований;
- замена переменной;
- универсальный метод.
Сущность всех этих методов состоит в том, чтобы избавиться от знака модуля, заменяя данное уравнение равносильной системой или совокупностью уравнений.
1.Уравнение вида |х| = а (а - действительное число).
Решение данного типа уравнений вытекает из определения модуля.
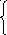 |х| = а х = + а, если а 0;
|х| = а х = + а, если а 0;
х = 0 , если а = 0;
х € 0 , если а
Звездный час (На столах у каждого карточки с номерами 1,2,3,4,5)
Попробуйте решить несколько уравнений непосредственно по определению модуля.
Выбрать верный ответ из предложенных вариантов. (По сигналу поднимаем карточку с номером правильного ответа)
1) | х | = 7; 2) | х | = -7; 3). | -х | = -7 4). | х - 7 | = 7 - х;
7;
-7;
7; -7
нет решений
другой ответ.
х ≤ 1
Поясним решение уравнений:
2,3 уравнения, очевидно, не имеют решений, так как модуль числа не может быть отрицательным;
в правой части 4-го уравнения стоит выражение, взятое из-под знака модуля со знаком « - ». Прямо из определения модуля следует, что такое возможно лишь тогда, когда это выражение неположительное, т.е. х - 7 ≤ 0 , значит, х ≤ 7.
Обратите внимание: ответ здесь не совсем обычный для уравнений – целая полупрямая |
2. Уравнение вида | f(х) | = а (а - действительное число)
 если а 0, то | f(х) | = а f(х) = а,
если а 0, то | f(х) | = а f(х) = а,
f(х) = - а
если а =0, то | f(х) | = а f(х) = 0,
если а
Пример №1. Решить уравнение: | х2 – 2х -4 | = 4;
 | х2 – 2х -4 | = 4 х2 – 2х -4 = 4;
| х2 – 2х -4 | = 4 х2 – 2х -4 = 4;
х2 – 2х -4 = -4.
1). х2 – 2х -4 = 4 2) х2 – 2х -4 = -4.
х = 4; х = 0;
х = -2. х = 2.
Ответ: 4; -2; 0; 2.
Задание: «Звездный час». «Выбираем равносильности».
Уравнения: а). | х2 – х + 1 | = 3; б) | х2 – х + 1 | = 0; в) | х2 – х + 1 | = -3.
Из предложенных вариантов выбираем соответствующие равносильности для каждого уравнения:
х 2 – х + 1 = 0;
2 – х + 1 = 0;
х2 – х + 1 = 3;
х2 – х + 1 = -3.
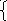 х2 – х + 1 = 3;
х2 – х + 1 = 3;
х2 – х + 1 = -3.
Другой ответ.
3. Уравнение вида | f(х) | = g(х)
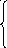 Из определения модуля следует, что корни уравнения должны удовлетворять условию g(х) ≥ 0. При соблюдении этого условия искомые корни уравнения должны удовлетворять совокупности f(х) = g(х) или f(х) = - g(х). Значит, уравнение равносильно
Из определения модуля следует, что корни уравнения должны удовлетворять условию g(х) ≥ 0. При соблюдении этого условия искомые корни уравнения должны удовлетворять совокупности f(х) = g(х) или f(х) = - g(х). Значит, уравнение равносильно
g(х) ≥ 0.
| f(х) | = g(х) f(х) = g(х)
f(х) = - g(х).
Пример №2.
| х2 –4 х + 3 | = 2х – 5.
|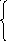
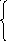 х2 –4 х + 3 | = 2х – 5. 2х -5 ≥ 0, х ≥ 2,5,
х2 –4 х + 3 | = 2х – 5. 2х -5 ≥ 0, х ≥ 2,5,
х2 –4 х + 3 = 2х – 5, х2 –6 х + 8 = 0,
х2 –4 х + 3 = -2х + 5, х2 –2 х - 2 = 0.

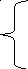 1). х2 –6 х + 8 = 0
1). х2 –6 х + 8 = 0
Х = 4 х ≥ 2,5,
Х = 2 х = 4
2). х2 –2 х - 2 = 0. х = 2
Д = 12 х = 1 + √3
х = 1 + √3 ( 2,7) х = 1 - √3
х = 1 - √3 ( - 0,7)


-0,7 2 2,5 4
Ответ: 4; 1 + √3
4. Уравнение вида |f(х) | = |g(х)|
Можно избавиться от модуля по определению, но есть более короткий путь решения.
Очевидно, что если равны модули двух чисел, то сами числа либо равны, либо противоположны, т.е. это уравнение равносильно совокупности уравнений:

|f(х) | = |g(х)| f(х) = g(х)
f(х) = - g(х).
Пример №3.
| х2 + 2 х - 1 | = |х + 1|.

| х2 + 2 х - 1 | = |х + 1| х2 + 2 х - 1 = х + 1 х2 + х - 2 = 0
х2 + 2 х - 1 | = |х + 1| х2 + 2 х - 1 = х + 1 х2 + х - 2 = 0
х2 + 2 х - 1 = - х – 1 х2 + 3 = 0
1) х2 + х - 2 = 0 2). х2 + 3 = 0
х = 1 х = 0
х = -2 х = -3.
Ответ: -3; -2; 0; 1.
Задание:
Найти ошибку:
|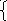 х + 3 | = |х2 - 1| х + 3 = х2 – 1
х + 3 | = |х2 - 1| х + 3 = х2 – 1
х + 3 = - х2 – 1.
5.Уравнения вида ах2 +b|х| +с =0
Пример № 5.
х2 - 3|х| +2 = 0
Предлагаю вам найти способ решения таких уравнений.
у=|х| , тогда у2 - 3у + 2 = 0
у = 1, у=2.
Значит, |х| = 1 или |х| = 2
х = 1 х = 2
х= -1 х= -2
Ответ: -2; -1; 1; 2.
6.Уравнения вида |х –а| + |х – b| = m
Решаются такие уравнения методом интервалов.
Находим корни подмодульных выражений, отмечаем их на координатной прямой.
На каждом из получившихся интервалов двучлены х-а и х-b сохраняют знак. Поэтому каждый из модулей раскрывается со своим знаком.
Рассмотрим исходное уравнение на каждом из промежутков и найденные решения объединяем.
Пример № 6.
| |х + 1| + |х – 4| =6
1. х+1 =0 х – 4 = 0
х = -1 х = 4
2.

 х – 4 - - +
х – 4 - - +

х + 1 - + +


 - 1 4
- 1 4
1). х
2). -1 ≤ х ≤ 4.В этом промежутке уравнение принимает вид х + 1 –х-4 =6, т.е. 0х =6. Следовательно, в данном интервале уравнение решений не имеет.
3) х4. Здесь имеем х + 1 + х – 4 =6, т.е. 2х = 9, х=4,5 . Это решение принадлежит рассматриваемому промежутку.
Объединение полученных решений дает ответ.
Ответ: 4,5; -1,5.
5. Организация первичного закрепления.
Итак, мы рассмотрели 6 типов уравнений и способы их решения (таблица).
|
| Типы уравнений
| Схемы решений |
| 1. | | х | = а (а - действительное число).
| 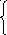 х = + а, если а 0; х = + а, если а 0; |х| = а х = 0 , если а = 0; х € 0 , если а
|
| 2. | | f(х) | = а (а - действительное число). |  если а 0, то | f(х) | = а f(х) = а, если а 0, то | f(х) | = а f(х) = а,
f(х) = - а если а =0, то | f(х) | = а f(х) = 0, если а
|
| 3. | | f(х) | = g(х)
| 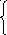 f(х) = g(х) f(х) = g(х) | f(х) | = g(х) f(х) = - g(х). g(х) ≥ 0.

|
| 4. | |f(х) | = |g(х)| | |f(х) | = |g(х)| f(х) = g(х) f(х) = - g(х).
|
| 5. | ах2 +b|х| +с =0 | Подстановка у = | х |
|
| 6. | |х –а| + |х – b| = m
| Метод интервалов. |
«Звездный час»
Задание: К какому типу относится каждое уравнение? (Таблица на доске и такие же карточки у учащихся)
Ребята отвечают на вопрос и заполняется столбец «Тип»
|
| Уравнения | Тип | Схема решения
|
| 1 | |х| + | х-1 | + | х-2| = 2
|
|
|
| 2 |
| х2 - х - 6 | = | 2х2 + х - 1|.
|
|
|
| 3 | | х2 –7 х + 1 | = х +1. |
|
|
| 4 | | х2 – 5х +1| = 5;
|
|
|
| 5 | х2 - 4|х| = - 3
|
|
|
6. Анализ. Прием «Пчелиный улей».
В парах обменяться мнениями о том, кто что узнал и не понял, учесть листок самоконтроля. Сформулировать вопросы, которые хотели бы задать. На карточках написать схемы решения каждого уравнения.
Каждая пара по очереди задает свой вопрос, на которые отвечает учитель или кто-то из учеников.
7. Постановка задания на дом.
Выучить лекцию, разобрать опорные задачи. Решить уравнения из карточки в тетрадях.
Подведение итогов, рефлексия.
Учащиеся сдают заполненный лист самоконтроля
Лист самоконтроля Ф.И. _________________________
|
| Задания | 1 | 2 | 3 | 4 | 5 | Кол-во правильн ответов |
| 1. | Определение модуля |
|
|
|
|
|
|
| 2. | Уравнение | х | = а |
|
|
|
|
|
|
| 3. | Уравнение | f(х) | = а |
|
|
|
|
|
|
| 4. | Уравнениие | f(х) | = |g(х)| |
|
|
|
|
|
|
| 5. | Определение типов уравнений |
|
|
|
|
|
|
Оценка _______
Этап рефлексии.
У каждого ученика карточки трех цветов на клейкой основе:
Карточка зеленого цвета обозначает: « Я удовлетворен уроком, урок был полезен для меня, я много с пользой работал на уроке, получил заслуженную оценку».
Карточка желтого цвета обозначает: «Урок был интересен, и я принимал в нем посильное участие, урок был в определенной степени полезен для меня, я сумел выполнить ряд заданий».
Карточка красного цвета обозначает: «Пользы от урока я получил мало, я не очень понимал, о чем идет речь, мне это не очень нужно, домашнее задание я не понял, к ответу на уроке я был не готов».
При выходе из класса учащиеся по желанию прикрепляют на доске карточку соответствующего цвета. Получается цветовой индекс урока.

 Получите свидетельство
Получите свидетельство Вход
Вход







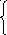 5. | а| = b b≥ 0,
5. | а| = b b≥ 0, если а 0, то | f(х) | = а f(х) = а,
если а 0, то | f(х) | = а f(х) = а,  | х2 – 2х -4 | = 4 х2 – 2х -4 = 4;
| х2 – 2х -4 | = 4 х2 – 2х -4 = 4;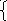 х2 – х + 1 = 3;
х2 – х + 1 = 3; Из определения модуля следует, что корни уравнения должны удовлетворять условию g(х) ≥ 0. При соблюдении этого условия искомые корни уравнения должны удовлетворять совокупности f(х) = g(х) или f(х) = - g(х). Значит, уравнение равносильно
Из определения модуля следует, что корни уравнения должны удовлетворять условию g(х) ≥ 0. При соблюдении этого условия искомые корни уравнения должны удовлетворять совокупности f(х) = g(х) или f(х) = - g(х). Значит, уравнение равносильно

 1). х2 –6 х + 8 = 0
1). х2 –6 х + 8 = 0 














 Урок математики "Решение уравнений с переменной под знаком модуля" (96 КB)
Урок математики "Решение уравнений с переменной под знаком модуля" (96 КB)
 0
0 2232
2232 334
334 Нравится
0
Нравится
0


