Пояснительная записка
За основу взято учебное пособие «Абсолютная величина» кафедры математики гимназии № 40 и учебное издание Голубева В.И. «Эффективные методы решения задач по теме «Абсолютная величина»» и книга «Абсолютная величина», автор- И.И. Гайдуков; издательство «Просвещение» 1964г.
Данная программа курса по выбору своим содержанием сможет привлечь учащихся 9 классов, которым интересна математика и которым хочется глубже и основательнее познакомиться с ее методами и идеями.
Программа курса предназначена для углубления знаний по математике, для поддержки основного базового курса, не нарушая его целостности, а также для ориентации учащихся в выборе профиля обучения и индивидуального образовательного пути.
Программа курса предусматривает изучение темы «Абсолютная величина», позволяет подробно познакомить учащихся с понятием модуля, детально разобрать алгоритмы построения модульных графиков, научить решать уравнения, содержащие знак абсолютной величины.
Выбранный данный курс предполагает рассмотреть примеры и задачи доступные школьникам 9 классов и затрагивает одну из самых популярных тем «абитуриентской» математики «Абсолютная величина».
Популярность этой темы обусловлена удивительными свойствами модуля числа, многие из которых совершенно не отражены как в учебниках, так и в многочисленных пособиях для поступающих в вузы.
«Приоткрыть завесу» тайны, увлечь девятиклассников эффективными методами решения задач по теме «Абсолютная величина» и составляет основную цель данного курса.
Курс рассчитан на 34 часа. Программой предусмотрено изучение теоретических вопросов, практикума по решению задач
Цель курса
Научить учащихся строить модульные графики и решать уравнения и неравенства, содержащие знак абсолютной величины.
Задачи курса
Формирование умения оперировать понятием модуля
Формирование способов самостоятельного приобретения знаний
Формирование способов логических рассуждений
Развитие графических навыков
Формирование навыков решения уравнений и неравенств.
Ожидаемые результаты
Учащиеся должны знать:
определение понятия «модуль»;
геометрическую интерпретацию понятия | а |;
основные свойства модуля;
эффективные методы решения задач, содержащих модуль.
алгоритмы построения модульных графиков
алгоритмы решения уравнений с модулем
алгоритмы решения неравенств с модулем
Учащиеся должны уметь:
упрощать выражения, содержащие модуль;
применять свойства модуля к решению задач;
применять алгоритмы для построения графиков;
строить модульные графики;
решать уравнения с модулем;
решать неравенства с модулем;
решать задачи, содержащие модуль.
Содержание курса
Определение. Геометрическая интерпретация понятия модуля. Основные свойства модуля. (1ч)
График функции у =f | х |. (2ч)
График функции у = |f(х)|. (2ч)
График функции у = |f(|х|)|. (2ч)
График функции |у| = f(х), где f(х) ≥ 0. (2ч)
График функции |у| = |f(х)|. (2ч)
Графики некоторых простейших функций, содержащих модуль. (2ч)
Построение графиков функции вида у = ||||х-а|-в|-с|-d|. (2ч)
Уравнения вида │f(х)│= а, а ≥ 0 (2ч)
Уравнения вида f│х│= а(2ч)
Уравнения вида │f(х)│= h(х) (2ч)
Эффективные методы решения задач, содержащих абсолютную величину.(3ч)
Неравенства с одним неизвестным.(2ч)
Неравенства с двумя неизвестными.(3ч)
Системы уравнений и неравенств.(4ч)
Итоговое занятие. Зачетная работа. (1ч).
Методические рекомендации по изучению курса.
Занятие №1
Понятие абсолютной величины. Абсолютная величина функции. Геометрическая интерпретация модуля. Основные свойства модуля. Приложение №1.
Занятие №2, 3,4
Графики функций, аналитическое выражение которых содержит знак абсолютной величины. График функции у = f(|х|). Симметричность графика функции относительно оси ординат. Приложение №2.
Занятие №5,6,7
График функции у =| f(х)|. Симметричность графика функции относительно оси абсцисс. Приложение №3
Занятие №8,9
График функции у =| f(|х|)|. Алгоритм построения. Преобразование участков графика, расположенных в нижней полуплоскости, в верхнюю полуплоскость симметрично относительно оси абсцисс. Приложение №4
Занятие №10-12
График функции |у| = f(х). Порядок построения графика. Симметричность относительно оси ОХ. Приложение №5
Занятие №13-16
График функции |у| = | f(х)|. Алгоритм построения графика. Симметричность относительно оси абсцисс. Приложение №6
Занятие №17-19
График функции у = | кх + в |. Определение абсолютной величины данной функции. Порядок построения графика. Симметричность относительно прямой х = -в/к. Приложение №7.
Занятие №20,21
График функции у = |||| х-а| - в| - с|-d|. Два способа построения графика (по определению модуля и использование преобразование графиков). Приложение №8.
Занятие №22-24
Уравнения с модулями. Уравнение вида | f(х)| = а, где а – число. Уравнение вида | f(х)| = |g(х)|.
Уравнение вида | f1(х)| +| f2(х)| +…| fn(х)| = g(х), (вместо знаков «+» могут стоять знаки «-»).
Свойства модуля и их обобщения. Разные эффективные методы решения задач. Приложение №9.
Занятие №25,26
Неравенства с одним неизвестным | f(х)| < а, | f(х)| > в, где а и в –неотрицательные числа, а f(х) - функция одного аргумента.
Занятие №27-29 Неравенства с двумя переменными. Графическое представление решений неравенств.
Занятие №30-33 Системы уравнений и неравенств. Графическое решение систем.
Весь материал - в документе.

 Получите свидетельство
Получите свидетельство Вход
Вход


 0
0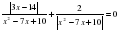
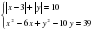









 Абсолютная величина (40.34 КB)
Абсолютная величина (40.34 КB)
 0
0 814
814 38
38 Нравится
0
Нравится
0




