1. Дробно-линейная функция и ее график.
Функция вида y = P(x) / Q(x) , где P(x) и Q(x) – многочлены, называется дробно-рациональной функцией.
С понятием рациональных чисел вы уже наверняка знакомы. Аналогично рациональные функции – это функции, которые можно представить как частное двух многочленов.
Если дробно-рациональная функция представляет собой частное двух линейных функций – многочленов первой степени, т. е. функцию вида y = (ax + b) / (cx + d) , то ее называют дробно-линейной.
Заметим, что в функции y = (ax + b) / (cx + d) , c ≠ 0 (иначе функция становится линейной y = ax/d + b/d) и что a/c ≠ b/d (иначе функция константа) . Дробно-линейная функция определена при всех действительных числах, кроме x = -d/c. Графики дробно-линейных функций по форме не отличаются от известного вам графика y = 1/x.
Кривая, являющаяся графиком функции y = 1/x, называется гиперболой. При неограниченном увеличении x по абсолютной величине функция y = 1/x неограниченно уменьшается по абсолютной величине и обе ветки графика приближаются к оси абсцисс: правая приближается сверху, а левая – снизу. Прямые, к которым приближаются ветки гиперболы, называются ее асимптотами.
Пример 1.
y = (2x + 1) / (x – 3) .
Решение.
Выделим целую часть: (2x + 1) / (x – 3) = 2 + 7/(x – 3).
Теперь легко видеть, что график этой функции получается из графика функции y = 1/x следующими преобразованиями: сдвигом на 3 единичных отрезка вправо, растяжением вдоль оси Oy в 7 раз и сдвигом на 2 единичных отрезка вверх.
Любую дробь y = (ax + b) / (cx + d) можно записать аналогичным образом, выделив «целую часть». Следовательно, графики всех дробно-линейных функций есть гиперболы, различным образом сдвинутые вдоль координатных осей и растянутые по оси Oy.

Для построения графика какой-нибудь произвольной дробно-линейной функции совсем не обязательно дробь, задающую эту функцию, преобразовывать. Поскольку мы знаем, что график есть гипербола, будет достаточно найти прямые, к которым приближаются ее ветки – асимптоты гиперболы x = -d/c и y = a/c.
Пример 2.
Найти асимптоты графика функции y = (3x + 5) /(2x + 2) .
Решение.
Функция не определена, при x = -1. Значит, прямая x = -1 служит вертикальной асимптотой. Для нахождения горизонтальной асимптоты, выясним, к чему приближаются значения функции y(x) , когда аргумент x возрастает по абсолютной величине.
Для этого разделим числитель и знаменатель дроби на x:
y = (3 + 5/x) / (2 + 2/x) .
При x → ∞ дробь будет стремиться к 3/2. Значит, горизонтальная асимптота – это прямая y = 3/2.
Пример 3.
Построить график функции y = (2x + 1) /(x + 1) .
Решение.
Выделим у дроби «целую часть»:
(2x + 1) / (x + 1) = (2x + 2 – 1) / (x + 1) = 2(x + 1) / (x + 1) – 1/(x + 1) = 2 – 1/(x + 1).
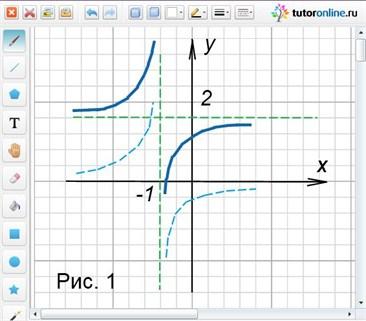
Теперь легко видеть, что график этой функции получается из графика функции y = 1/x следующими преобразованиями: сдвигом на 1 единицу влево, симметричным отображением относительно Ox и сдвигом на 2 единичных отрезка вверх по оси Oy.
Область определения D(y) = (-∞; -1) ᴗ(-1; +∞) .
Область значений E(y) = (-∞; 2) ᴗ(2; +∞) .
Точки пересечения с осями: c Oy: (0; 1) ; c Ox: (-1/2; 0). Функция возрастает на каждом из промежутков области определения.
Весь материал - в документе.

 Получите свидетельство
Получите свидетельство Вход
Вход











 Материал по математике на тему "Графики и их функции" (0.11 MB)
Материал по математике на тему "Графики и их функции" (0.11 MB)
 0
0 1106
1106 34
34 Нравится
0
Нравится
0





