Уравнения и неравенства с модулем в курсе 9 класса

Программа курса: « Уравнения и неравенства с модулем в курсе 9 класса»

Цель курса: Создание целостного представления о теме “Модуль», подготовить учащихся к успешному решению уравнений и неравенств с модулем, содержащих в заданиях ЕГЭ

Задачи курса:

Систематизировать ранее полученные знания о модуле.

Расширить спектр задач, посильных для учащихся.

Научить оценивать свои возможности по математике, и более осознано выбирать профиль дальнейшего обучения.

Совершенствовать и развивать математические знания и умения, повышать интерес к математике.

№ п/п

Тема

1

2

Количество часов

Модуль числа (понятие, определение, применение в других областях науки и техники). Простейшие уравнения с модулем (решение уравнений по определению

Решение уравнений с модулем (продолжение). Уравнения, содержащие два модуля

1ч

3

4

Уравнения, содержащие два модуля и более модуля

1ч

Неравенства с модулем

2ч

5

1ч

Графики функций, содержащие модуль

6

Простейшие системы уравнений и неравенств с модулем

7

1ч

2ч

Решение простейших уравнений и неравенств с модулем

2ч

Тема 1. Модуль числа (понятие, определение, применение в других областях науки и техники). Простейшие уравнения с модулем (решение уравнений по определению). Решение простейших уравнений с модулем вида:

Определение : абсолютной величиной (или модулем)

числа, называется:

.

Задачи для самостоятельной работы.

Решите уравнения, используя определение модуля.

.

.

|

.

.

.

Решите уравнение.

.

При решении уравнений вида традиционным способом, в несложных случаях можно возвести обе части уравнения в квадрат, избавившись от модуля и получив равносильное уравнение

Задачи для самостоятельной работы.

Решите уравнение:

2

При решении уравнений, содержащих два или более модулей можно использовать, кроме обычных способов, метод интервалов.

Решение. 1. Найдем значения переменной, при которых подмодульные

выражения обращаются в нуль:

Пример 1 : Решить уравнение

Определим знаки подмодульных выражений на трех образовавшихся промежутках :

+ +

+ -

- -

-4/3 3 х

3. Оба модуля раскрываются со знаком «+»

Первый модуль раскрываем со знаком « + » , а второй – со знаком « - »

система не имеет решений

Оба модуля раскрываются со знаком «-»

Ответ:

Пример 2. Решить уравнение

Решение. 1. Раскрываем внутренний модуль со знаком «+»

или

.

  Раскрываем внутренний модуль со знаком «-»

или

система не имеет решений. система не имеет решений.

Ответ: нет решений

Решите уравнение:

Найдите разность между наибольшим и наименьшим корнем уравнения:

Решите уравнение:

Найдите сумму корней уравнения:

Решите уравнение:

Решение неравенств вида:

Принцип решения неравенств, содержащих модули, аналогичен решению соответствующих уравнений. Отличие состоит в том, что при решении уравнений широко используется проверка, а при решении неравенств это часто вызывает затруднения. Следовательно, при решении неравенств необходимо использовать равносильные переходы, некоторые неравенства решаются с помощью замены переменной. Но более рационально - перейти к двойному неравенству или к равносильной системе двух неравенств

а также переходя к равносильной совокупности двух неравенств

Решит e неравенство и для каждого укажите наименьшее положительное число:

Решит e неравенство:

Тема 5. Построение графиков функций

Построение графика функции :

части графика функции

лежащие выше оси ОХ и на оси ОХ, остаются без изменения, а лежащие ниже оси ОХ – симметрично отражаются относительно этой оси (вверх) .

неотрицательна (ее график расположен в

верхней полуплоскости).

Замечание: функция

Построение графика функции :

часть графика функции

лежащая левее оси ОУ , удаляется, а часть, лежащая правее оси ОУ - остается без изменения и, кроме того, симметрично отражается относительно оси ОУ (влево). Точка графика, лежащая на оси ОУ, остается неизменной.

Замечание: функция

четная (её график симметричен относительно оси ОУ).

Пример 1. Построить график функции у =

Построение. 1. Построим график функции у = 2 х.

у

3

-3

2

-2

1

-1

0

-1

1

-2

2

-3

3

х

Построим график функции, у =

: часть графика функции

лежащая выше оси О х и на оси О х , остается без изменения, а лежащая ниже оси О х – симметрично отражаются относительно этой оси (вверх).

у

-3

3

-2

2

1

-1

0

1

-1

2

-2

3

-3

х

Построить график функции: у =

У=

У=

У =

У =

У =

У=

Система уравнений и неравенств с модулем решаются традиционным способом. Часто решение “одиночных” уравнений сводится к решению равносильных им систем, содержащих как уравнения, так и неравенства при этом может использоваться и графический метод решения систем уравнений и неравенств.

Пример 1. Решить систему двух неравенств с одной переменной

Решение .

Ответ: (-4;4).

Часто решение « одиночных » уравнений сводится к решению равносильных им систем, содержащих как уравнения, так и неравенства при этом может использоваться и графический метод решения систем уравнений и неравенств.

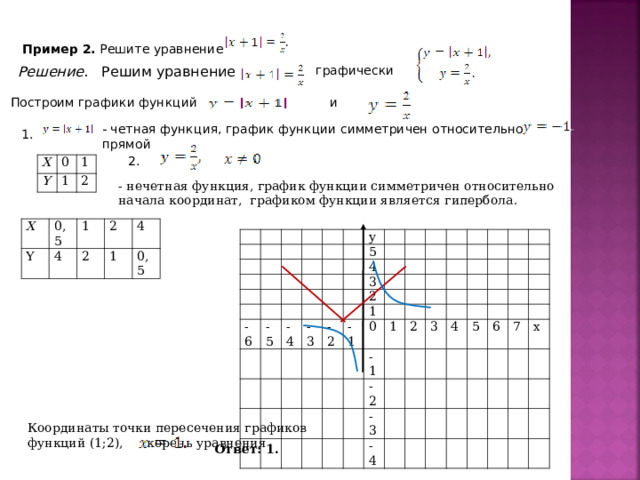
Пример 2. Решите уравнение

Решение . Решим уравнение

графически

и

Построим графики функций

- четная функция, график функции симметричен относительно прямой

1.

2.

X

0

Y

1

1

2

- нечетная функция, график функции симметричен относительно начала координат, графиком функции является гипербола.

X

Y

0,5

4

1

2

2

1

4

0,5

-6

у

5

-5

4

-4

-3

3

-2

2

1

-1

0

-1

1

2

-2

3

-3

4

-4

5

6

7

х

Координаты точки пересечения графиков функций (1;2), корень уравнения

Ответ: 1.

Решите систему уравнений:

Решите систему неравенств:

Решите уравнение графически:

3 |2х+1| |3х-2| (х-1)|х|-2х+2≤0 х-3|х-1|-1≤0 (х+4)|х|-3х-60 х-2|х|-3≥0 3х|2х-3|+7х-8 х-|5х+1|+50 " width="640"

Задачи для самостоятельной работы.

  Решить уравнение:

1. |3х+2|=1 7. |х-4х|=3х-6

2. |4х-1|=1 8. |х-8х+12|=3х-12

3. |5х-2|=2 9. |х-2х-8|=8х-8

4. 3х-5 = 1 10. |х+8х|=6х+24

|х-1|-4

5. |х-2|+1 = -1

2х+1 11. |х-2х-3|=3х-3

6. 7+ 3 х = -1

|х+1|-6 12. |х-3х|=4х-6

Решить неравенство:

• |х-1|3
• |2х+1|
• |3х-2|
• (х-1)|х|-2х+2≤0
• х-3|х-1|-1≤0
• (х+4)|х|-3х-60
• х-2|х|-3≥0
• 3х|2х-3|+7х-8
• х-|5х+1|+50