Получите свидетельство
Вход
Теорема Пифагора.
Решение задач
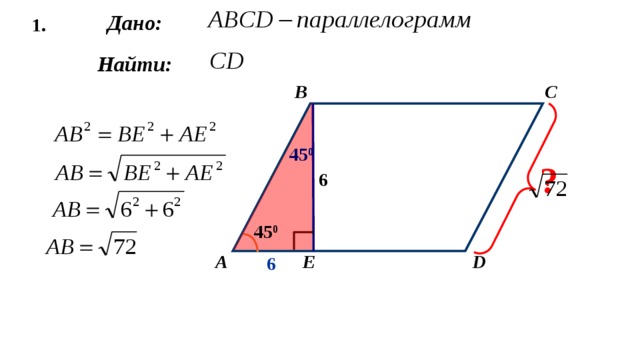
1.
Дано:
Найти:
C
B
45 0
?
6
45 0
Е
D
А
6
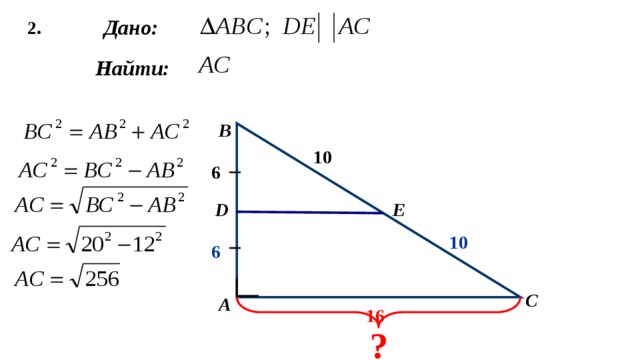
2.
Дано:
Найти:
B
10
6
Е
D
10
6
C
А
16
?
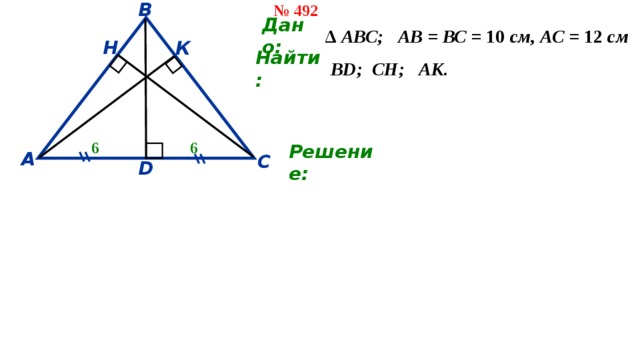
№ 492
В
∆ АВС; АВ = ВС = 10 см, АС = 12 см
Дано:
Н
К
Найти:
ВD; СН; АК.
6
6
А
С
Решение:
D
ВD – высота и медиана, = АD = DC = 6 см. 2. ∆АВD – прямоугольный ( L D = 90º), = по т. Пифагора: " width="640"
№ 492
В
Дано:
∆ АВС; АВ = ВС = 10 см, АС = 12 см
Н
К
ВD; СН; АК.
Найти:
10
6
6
А
С
Решение:
D
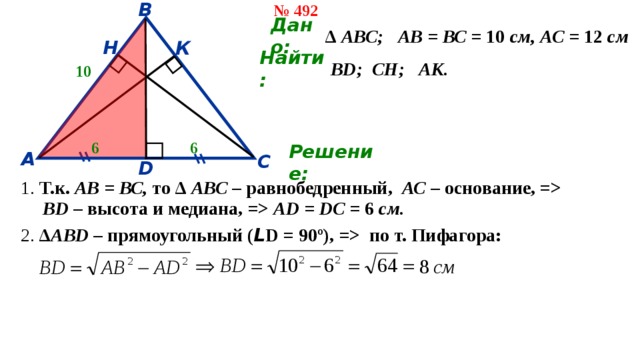
1. Т.к. АВ = ВС, то ∆ АВС – равнобедренный, АС – основание, =
ВD – высота и медиана, = АD = DC = 6 см.
2. ∆АВD – прямоугольный ( L D = 90º), = по т. Пифагора:
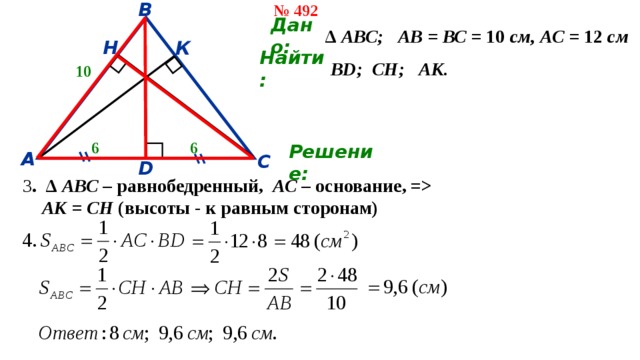АК = СН (высоты - к равным сторонам) " width="640"
№ 492
В
∆ АВС; АВ = ВС = 10 см, АС = 12 см
Дано:
Н
К
Найти:
ВD; СН; АК.
10
6
6
А
С
Решение:
D
3 . ∆ АВС – равнобедренный, АС – основание, =
АК = СН (высоты - к равным сторонам)
КЕ = 10 см, 3. ∆ АDК – прямоугольный,= " width="640"
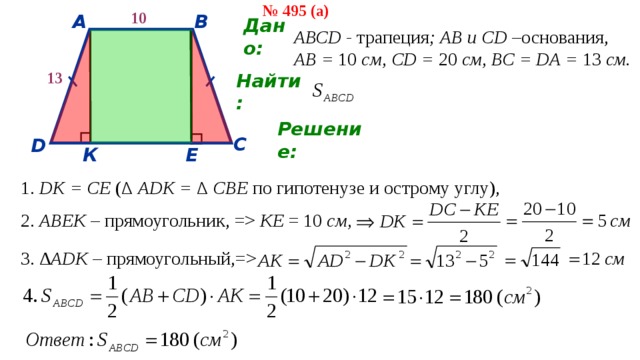
№ 495 (а)
10
В
А
АВСD - трапеция ; АВ и СD – основания, АВ = 10 см, СD = 20 см, ВС = DA = 13 см.
Дано:
13
Найти:
Решение:
С
D
К
E
1. DK = СE ( ∆ АDK = ∆ СВE по гипотенузе и острому углу),
2. АВЕК – прямоугольник, = КЕ = 10 см,
3. ∆ АDК – прямоугольный,=
Теорема Пифагора. Решение задач (140.07 KB)
0
1529
78
Нравится
0
