Теорема о трех перпендикулярах

«Теорема о трех перпендикулярах, ее применение при решении задач»

«Расскажи мне, и я забуду, покажи мне, и я запомню, дай мне сделать самому, и я пойму» О. Хайям

ЦЕЛЬ УРОКА

ОБУЧАЮЩАЯ

• обосновать необходимость теоремы о трех перпендикулярах
• сформировать видение изученной закономерности в различных ситуациях: при решении задач на доказательство или задач, требующих найти численное (или буквенное значение) какого-либо элемента .
• учиться умению читать чертеж,
• учить умению объяснять, комментировать выполняемое упражнение в виде цельного связного рассказа.

РАЗВИВАЮЩАЯ :

• способствовать развитию общения как метода научного познания, аналитико-синтетического мышления, смысловой памяти и произвольного внимания, развитие навыков исследовательской деятельности (планирование, выдвижение гипотез, анализ, обобщение).
• способствовать развитию общения как метода научного познания, аналитико-синтетического мышления, смысловой памяти и произвольного внимания,
• развитие навыков исследовательской деятельности (планирование, выдвижение гипотез, анализ, обобщение).

ВОСПИТАТЕЛЬНАЯ :

• развивать у учащихся коммуникативные компетенции,
• способствовать развитию творческой деятельности учащихся, потребности к самообразованию.

ПЛАН УРОКА

1. . Организационный момент.

Проверка домашнего задания.

2.

3. Актуализация знаний.

4. Применение теории на практике.

5. Самостоятельное выполнение учащимися заданий

6. Подведение итогов.

7 . Домашнее задание.

Суть метода отпративного состоит в следующем:

1. Сначала делается, предположение противоположное тому, что требуется доказать. 2. Затем выясняется, что следует из сделанного предположения на основании уже приобретенных теоретических знаний (теорем, аксиом и т.д.). 3. Устанавливается несоответствие (противоречие) предположения с теоретическими данными. 4. Делается вывод о том, что наше предположение не верно , а верно у тверждение ему противоположное, т.е. то, что требуется доказать.

SB. Из прямоугольных треугольников SOA и SOB: Получаем: ОАOB. Между тем ОА S В А О С t " width="640"

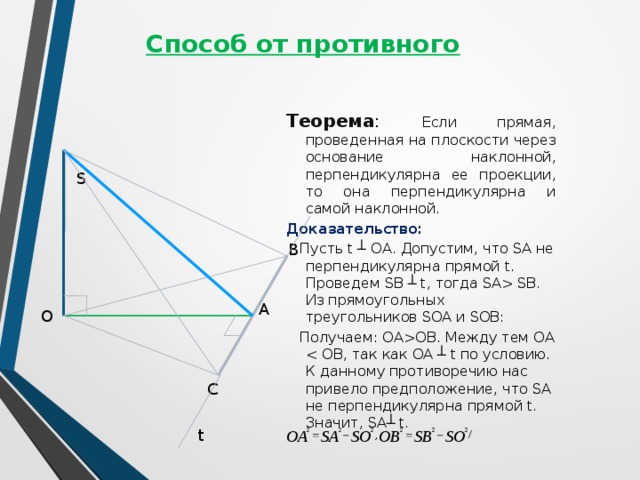
Способ от противного

Теорема : Если прямая, проведенная на плоскости через основание наклонной, перпендикулярна ее проекции, то она перпендикулярна и самой наклонной.

Доказательство:

Пусть t ┴ ОА. Допустим, что SA не перпендикулярна прямой t. Проведем SB ┴ t, тогда SA SB. Из прямоугольных треугольников SOA и SOB:

Получаем: ОАOB. Между тем ОА

S

В

А

О

С

t

Способ -свойства равнобедренного треугольника

Доказательство:

От точки А отложим равные отрезки: АМ= АN. Точки М и N соединим с точками O и S. В ОА есть одновременно высота и медиана, этот треугольник равнобедренный: ОМ = ОN. Прямоугольные треугольники OSM и OSN равны (по двум катетам). Из их равенства следует, что SM= SN и SA- медиана равнобедренного треугольника MSN. Значит, SA одновременно и высота этого треугольника, т. е. SA┴MN.

S

M

O

A

t

N

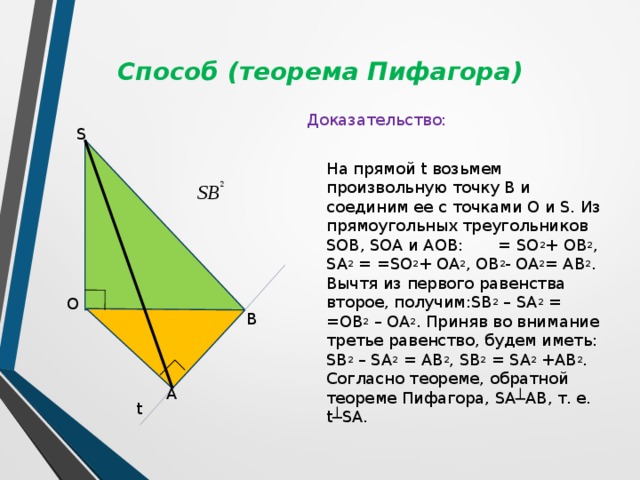
Способ (теорема Пифагора)

Доказательство:

На прямой t возьмем произвольную точку В и соединим ее с точками О и S. Из прямоугольных треугольников SOB, SOA и AOB: = SO 2 + OB 2 , SA 2 = =SO 2 + OA 2 , OB 2 - OA 2 = AB 2 . Вычтя из первого равенства второе, получим:SB 2 – SA 2 = =OB 2 – OA 2 . Приняв во внимание третье равенство, будем иметь: SB 2 – SA 2 = AB 2 , SB 2 = SA 2 +AB 2 . Согласно теореме, обратной теореме Пифагора, SA┴AB, т. е. t┴SA.

S

O

B

A

t

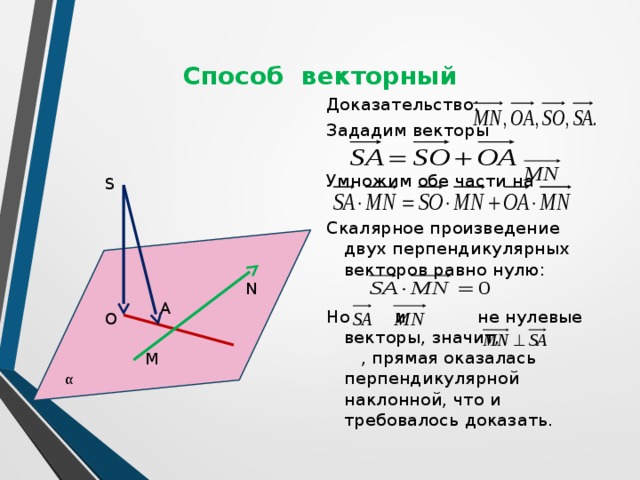
Способ векторный

Доказательство:

Зададим векторы

Умножим обе части на

Скалярное произведение двух перпендикулярных векторов равно нулю:

Но и не нулевые векторы, значит, , прямая оказалась перпендикулярной наклонной, что и требовалось доказать.

S

N

A

O

M

α

Актуализация опорных знаний.

1. Угол между прямыми равен 90˚. Как называются такие прямые?

Ответ : перпендикулярные.

2. Верно ли утверждение: «прямая называется перпендикулярной плоскости, если она перпендикулярна некоторой прямой, лежащей этой плоскости»

Ответ: да.

3. Сформулируйте признак перпендикулярности прямой и плоскости.

Ответ: если пряма перпендикулярна к двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна к этой плоскости.

4. Как определяется расстояние от точки до прямой на плоскости?

Ответ: как длина перпендикуляра, проведённого из точки к данной прямой.

5. По рисунку назовите:

перпендикуляр, основание

перпендикуляра, наклонную к

плоскости α, основание

наклонной и её проекцию на

плоскость α.

6. Сформулируйте теорему о трёх перпендикулярах .

P

D

K

α

А

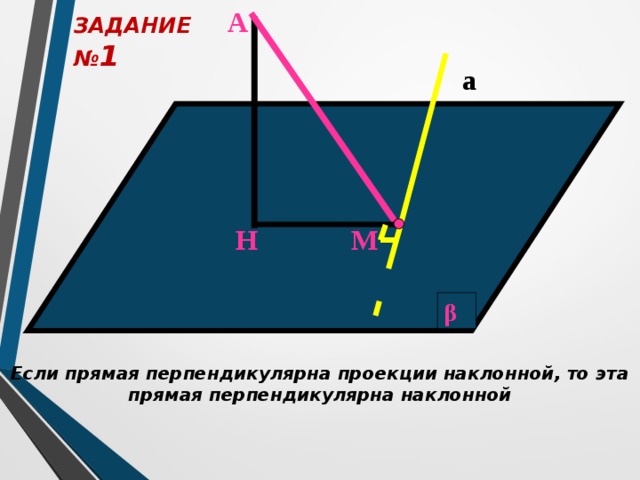
ЗАДАНИЕ № 1

а

Н

М

β

Если прямая перпендикулярна проекции наклонной, то эта прямая перпендикулярна наклонной

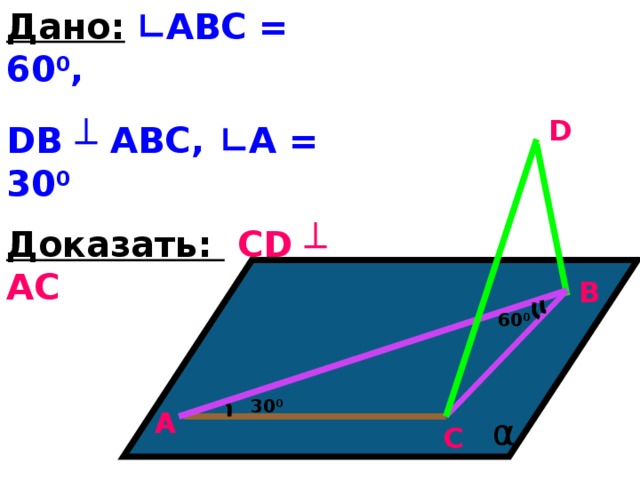
Дано: ∟АВС = 60 0 ,

DB ┴ ABC, ∟A = 30 0

Доказать: CD ┴ AC

D

B

60 0

30 0

A

α

C

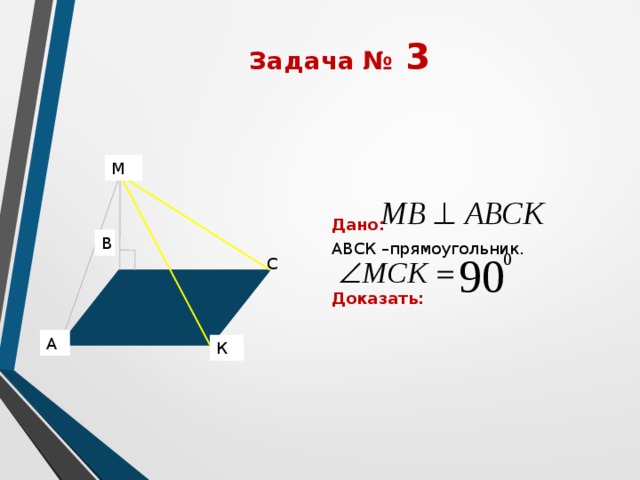
Задача № 3

Дано:

АВСК –прямоугольник.

Доказать:

М

В

С

А

К

C

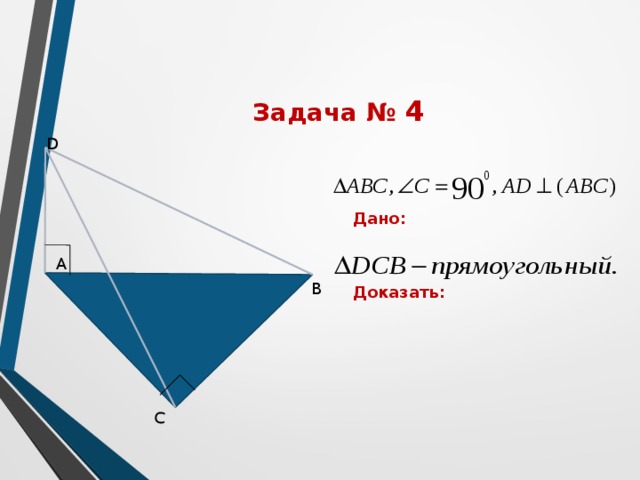
Задача № 4

D

Дано:

Доказать:

A

B

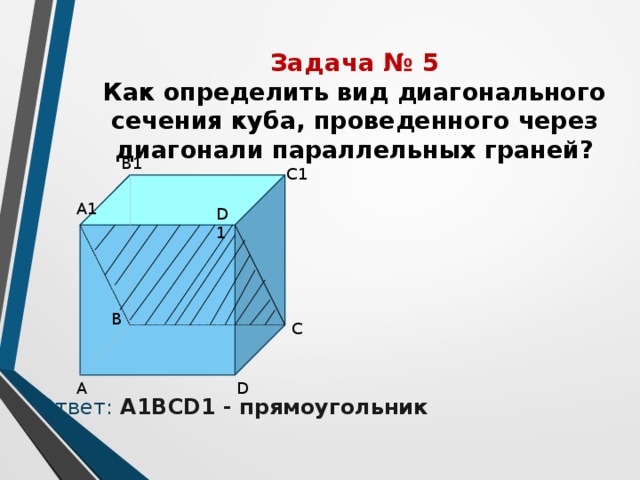
Задача № 5 Как определить вид диагонального сечения куба, проведенного через диагонали параллельных граней?

Ответ: А1ВСD1 - прямоугольник

В1

С1

А1

D1

В

C

D

А

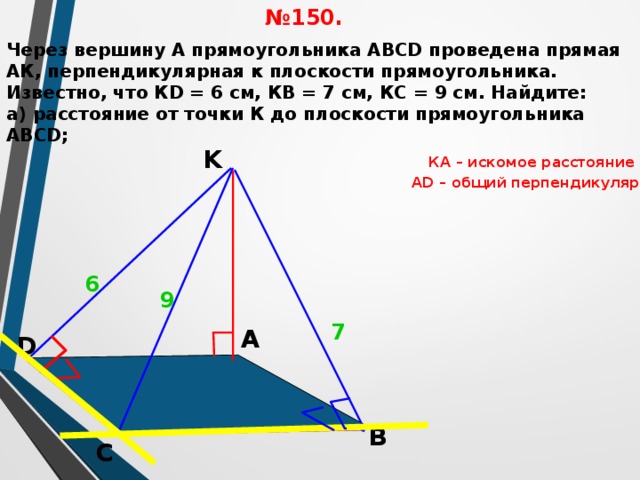
№ 150.

Через вершину А прямоугольника АВСD проведена прямая АК, перпендикулярная к плоскости прямоугольника. Известно, что КD = 6 см, КВ = 7 см, КС = 9 см. Найдите:

а) расстояние от точки К до плоскости прямоугольника АВСD;

K

КА – искомое расстояние

АD – общий перпендикуляр

6

9

Л.С. Атанасян №150.

7

А

D

В

С

17

• Руководитель одного из учреждений, прежде чем заасфальтировать дорожку ведущую к остановке. Оставил газоны нетронутыми.

Изучить местность по рисунку и сделать заключение об эффективности строительства дорожки от здания к остановке и определить место где удобно будет садиться в автобус.

Домашняя работа

• П. 20
• № 149

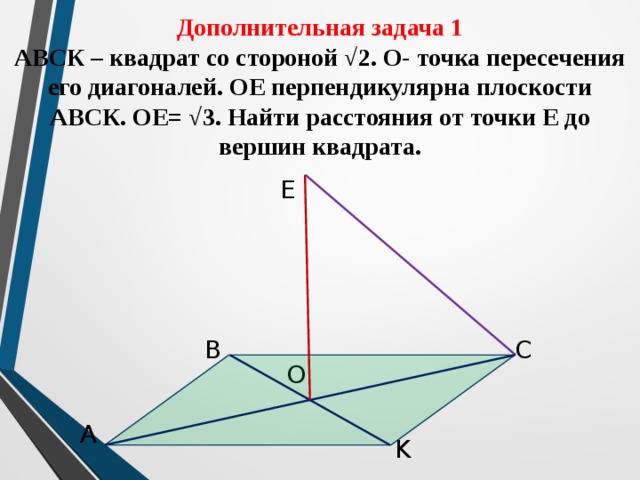
Дополнительная задача 1 АВСК – квадрат со стороной √2. О- точка пересечения его диагоналей. ОЕ перпендикулярна плоскости АВСК. ОЕ= √3. Найти расстояния от точки Е до вершин квадрата.

Е

В

С

О

А

K

D

1.вариант

2.-вариан

D

В

В

А

А

С



С



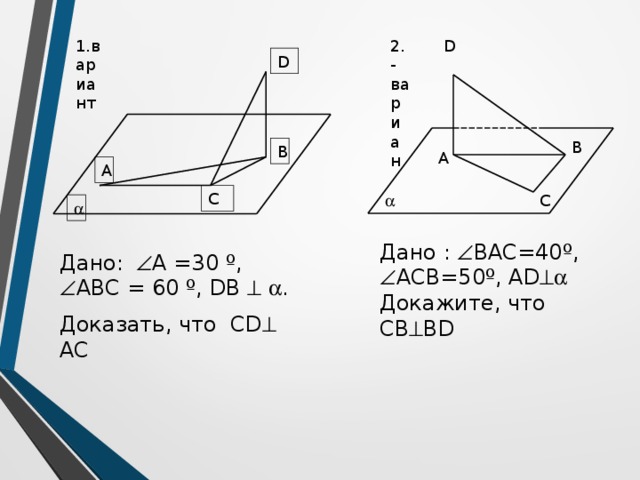
Дано :  BAC=40º,  ACВ=50º, АD 

Докажите, что СВ  BD

Дано:  А =30 º,  АВС = 60 º, DB   .

Доказать, что CD  AC