Урок геометрии в 10 классе
учитель Грабок С.А.
Республика Казахстан г. Актобе ОСШ № 25
Тема урока: Перпендикулярность прямой и плоскости в пространстве.
Цель урока:
-Закрепить изученный теоритический материал на практике.
-Уметь применять знание признаков перпендикулярности прямой и плоскости; наклонной и перпендикуляра к плоскости; теоремы о трех перпендикулярах при решении задач
- Учиться умению читать чертеж
- Учиться умению объяснять, комментировать .
- Развивать логическое мышление, пространственное изображение, вычислительные навыки.
- Развивать у учащихся коммуникативные компетенции (умение работать в группах, парах, элементы ораторского искусства)
-Обеспечение психологической комфортности, самостоятельной деятельности и инициативе учащегося
План урока
I Организационный момент.
II Актуализация знаний.
III Применение теории на практике.
IV Работа в парах.
V Самостоятельная работа.
VI Работа в группах с задачами различного уровня.
VII Подведение итогов.
VIII Домашнее задание.
Оснащение урока: компьютер, мультимедийный проектор, карточки для групповой работы, карточки для работы в парах.
Методы обучения: словесный, наглядный, практический.
Формы организации познавательной деятельности учащегося: фронтальная работа с классом, парная работа, самостоятельная работа.
Ход урока.
Учитель: Работа, вы думаете, что важнее в геометрии теория или практика? Ответы уч-ся.
Учитель: Так как мнения разделились, то я предлагаю вам ответить, но этот вопрос в конце урока. А сейчас повторим теоретический материал, выполнив тест.
1. Актуализация знаний (тест).
1.Если угол между двумя прямыми равен 90°, то эти прямые:.......
2. Прямая называется перпендикулярной к плоскости, если она ....... к любой прямой, лежащей в
этой плоскости.
3. Если две прямые перпендикулярны к плоскости, то они .........
4. Если прямая перпендикулярна к двум ......прямым, лежащим в плоскости, то она
перпендикулярна к этой плоскости.
5. Перпендикуляр, проведенный из данной точки к плоскости, меньше любой......проведенной из
этой же точки к этой плоскости.
6. Длина перпендикуляра, проведенного из точки к плоскости, называется...... от точки до
плоскости.
7. Прямая, проведенная в плоскости через основание наклонной перпендикулярна к ее .......
перпендикулярна и самой наклонной.
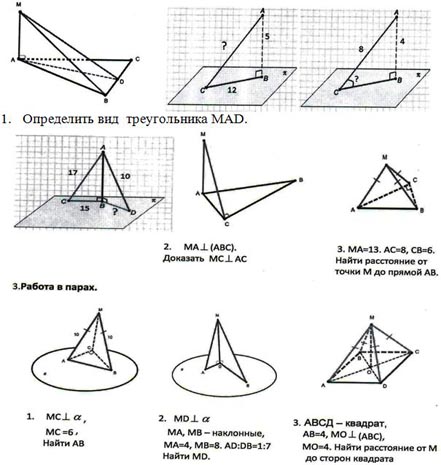
2. Применение теории на практике.
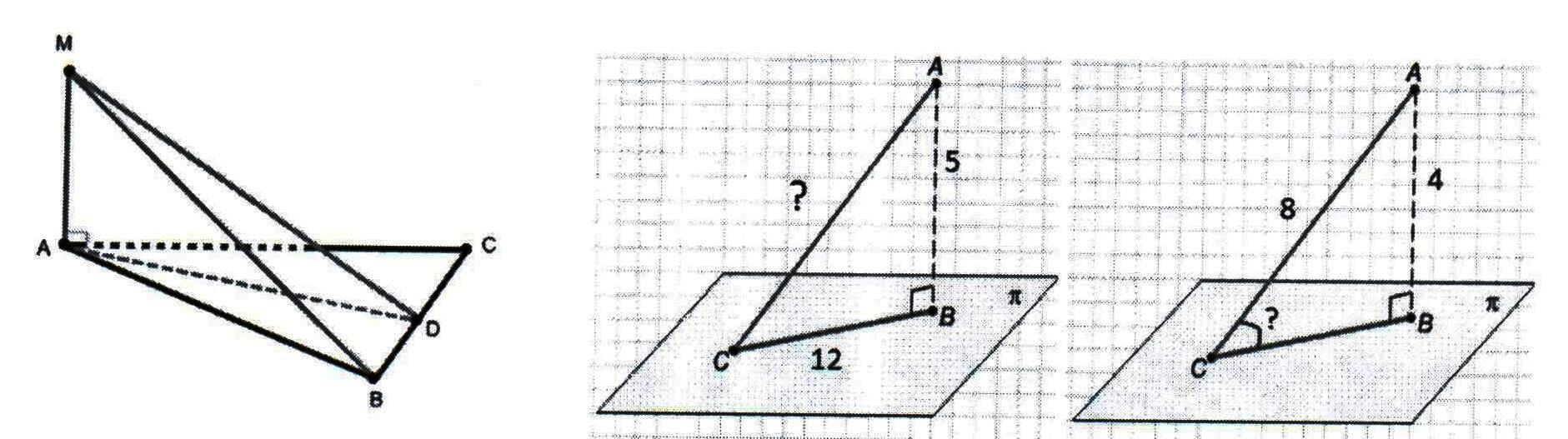
1. Определить вид треугольника MAD.
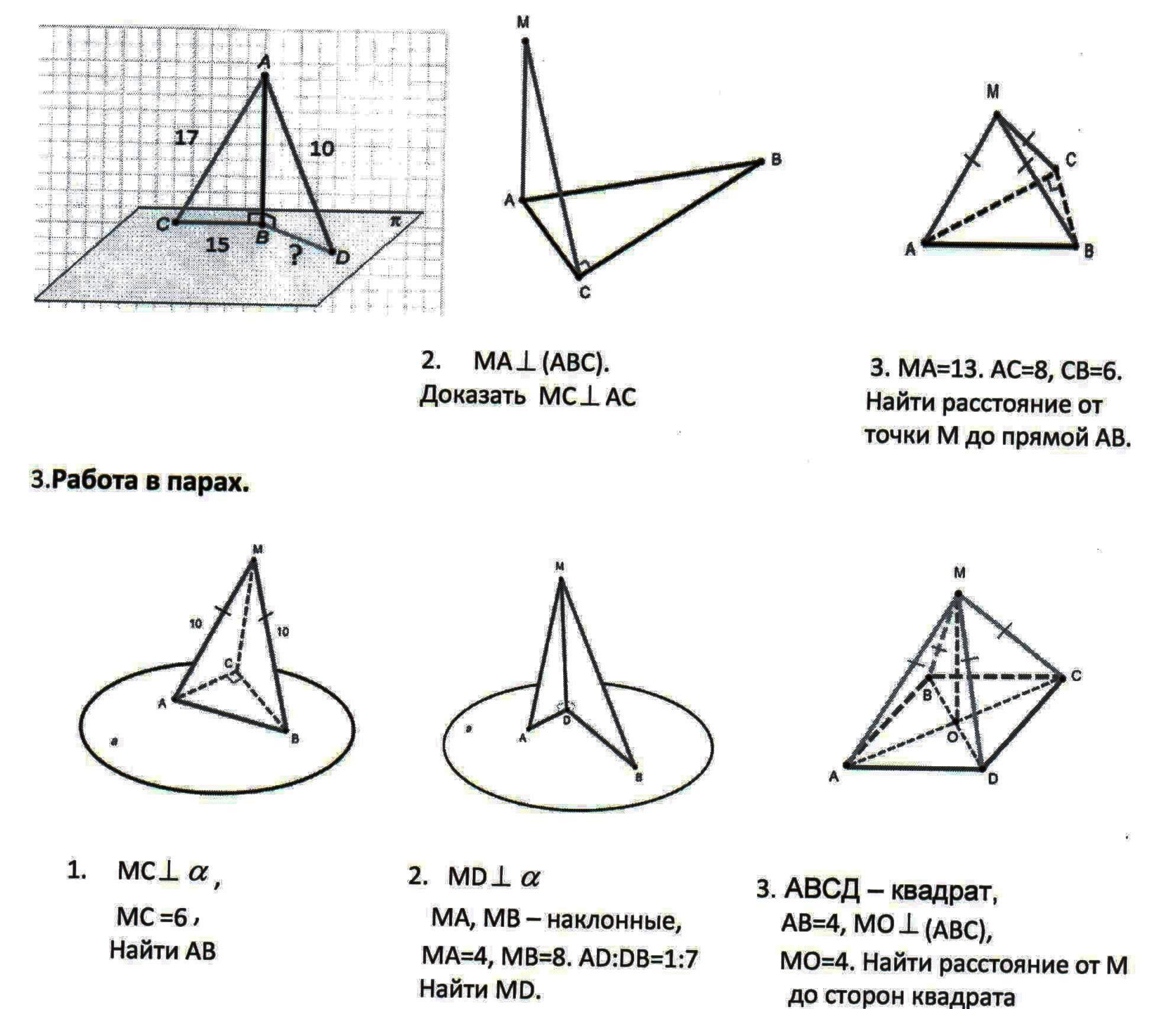
В парах один из учеников помогает решать задачи второму ученику, если пара равносильная, то ей может помочь учитель.
4.Самостоятельная работа предлагается некомпетентным учащимся и имеющим минимальный или общий уровень подготовки.
1 вариант.
1.Из точки плоскости проведены две наклонные. Найти длины наклонных, если они относятся как 1: 2, а соответствующие им проекции равны 1см и 7см.
2.Треугольник ABC равносторонний со стороной, равной 18см. Точка М удалена от вершин треугольника на 12см. Найти расстояние отточки М до плоскости ABC.
3. Дан равнобедренный треугольник ABC с основанием АС= 10см и боковыми сторонами АВ=ВС= 13см. Из вершины В проведен перпендикуляр ВМ= 2см к плоскости треугольника. Найти расстояние от точки М до стороны АС треугольника ABC.
2 вариант.
1. Из точки к плоскости проведены две наклонные, которые относятся как 5:6. Найдите расстояние отточки до плоскости, если соответствующие проекции наклонных равны 4см и 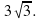
2. Треугольник ABC равносторонний со стороной, равной 6см. Точка М удалена от вершин треугольника на 4см. Найти расстояние отточки М до плоскости ABC.
3. Дан равнобедренный треугольник ABC с основанием АС= 40см и боковыми сторонами АВ=ВС=25см. Из вершины В проведен перпендикуляр ВМ= 5см к плоскости треугольника. Найти расстояние отточки М до стороны АС треугольника ABC.
5.Работа в группах (с учащимися имеющими общий уровень планируемых результатов и учеников, вышедших на продвинутый уровень и совершенствующееся в нем)
Уровень А
1. Через точки А и В проведены прямые, перпендикулярные к плоскости  , пересекающие ее в точках С и D соответственно. Найти расстояние между точками А и В, если АС= 21,5см, BD= 33.5см, CD= 9см и отрезок АВ не пересекает плоскость
, пересекающие ее в точках С и D соответственно. Найти расстояние между точками А и В, если АС= 21,5см, BD= 33.5см, CD= 9см и отрезок АВ не пересекает плоскость  .
.
2. Из точки К к плоскости проведены две наклонные, одна из которых равна 12см и образует с плоскостью угол 60°. Найти длину второй наклонной, если ее проекция на плоскость равна 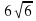 см.
см.
3. Из центра О правильного треугольника KLB со стороной 4см проведен перпендикуляр ОМ к плоскости треугольника. Вычислите расстояние отточки М до одной из сторон треугольника, если ОМ= 2см.
Уровень В.
Точка S не принадлежит плоскости треугольника ABC; AC┴ВС; SA=SB=SC= 10см; СМ= 5см- медиана;
Найти: расстояние от точки S до плоскости треугольника ABC.
2. Из вершины В треугольника ABC проведен перпендикуляр BD к плоскости этого треугольника. Вычислите расстояние отточки D до прямой АС и площадь треугольника ACD, если BD= 9см, ВА=ВС= 13см; АС= 10см.
3. Стороны треугольника равны 13см, 14см и 15см. Точка М, расположенная вне плоскости треугольника, удалена от всех сторон треугольника на 5см. Определите расстояние отточки М до плоскости треугольника.
Уровень С.
1. Из данной точки М к данной плоскости проведены две наклонные, образующие с этой плоскостью углы 30° и 60° градусов, а между собой угол 90°. Расстояние отточки М до плоскости равно 4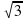 см. Найти расстояние между основаниями наклонных.
см. Найти расстояние между основаниями наклонных.
2. Из вершины М треугольника МКС проведен перпендикуляр MN к плоскости этого треугольника. Вычислите расстояние отточки N до прямой КС и площадь треугольника NKC, если КМ=МС= 10см; КС= 16см;
MN= 3 см.
3. Диагонали ромба равны 30 и 40см и пересекаются в точке М. Длина перпендикуляра ВМ к плоскости ромба =5см. Найти расстояние от точки В до каждой стороны ромба.
б.Подведение итогов урока. Рефлексия.
Учитель: Сегодня на уроке мы повторили перпендикулярность прямых в пространстве, прямой и плоскости; перпендикуляр и наклонную, теорему о трех перпендикулярах, а это очень важный материал. На их применении основывается решение многих задач, и мы в этом убедились. Как вы думаете, что же все-таки важнее теория или практика? Да, действительно они неотделимы. Как говорил А.Н. Крылов «Теория без практики мертва или бесплодна; практика без теории невозможна или пагубна. Для теории нужны знания, для практики, сверх всего того, - умение»
7. Домашнее задание. 1. В треугольнике ABC AC=BC=4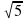 см, АВ =4
см, АВ =4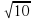 см. К плоскости треугольника проведен перпендикуляр ВК, равный 2
см. К плоскости треугольника проведен перпендикуляр ВК, равный 2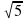 см. Найдите расстояние отточки К до прямой АС.
см. Найдите расстояние отточки К до прямой АС.
2. Стороны треугольника равны 10 см, 17 см и 21 см. Из вершины большего угла этого треугольника к его плоскости проведен перпендикуляр, равный 15 см. Найдите расстояние от его концов до прямой, которой принадлежит наибольшая сторона.

 Получите свидетельство
Получите свидетельство Вход
Вход





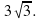
 , пересекающие ее в точках С и D соответственно. Найти расстояние между точками А и В, если АС= 21,5см, BD= 33.5см, CD= 9см и отрезок АВ не пересекает плоскость
, пересекающие ее в точках С и D соответственно. Найти расстояние между точками А и В, если АС= 21,5см, BD= 33.5см, CD= 9см и отрезок АВ не пересекает плоскость 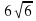 см.
см.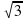 см. Найти расстояние между основаниями наклонных.
см. Найти расстояние между основаниями наклонных.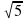 см, АВ =4
см, АВ =4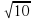 см. К плоскости треугольника проведен перпендикуляр ВК, равный 2
см. К плоскости треугольника проведен перпендикуляр ВК, равный 2








 Конспект урока по математике "Перпендикулярность прямой и плоскости в пространстве" (0.41 MB)
Конспект урока по математике "Перпендикулярность прямой и плоскости в пространстве" (0.41 MB)
 0
0 1839
1839 380
380 Нравится
0
Нравится
0




