Угол между прямой и плоскостью

Цели урока:

Образовательная: обобщить, систематизировать знания учащихся об углах между прямой и плоскостью; продолжить формирование умений и навыков в в решении  задач по данной теме.

Развивающая: углубление знаний, умений и навыков, знакомство с различными методами (геометрическим, векторно-координатнм, методом дополнительных построений); развитие творческой деятельности: интуиции, пространственного воображения, смекалки.

Воспитательная: приучать к эстетическому оформлению записи в тетради, прививать аккуратность и трудолюбие.

Устная работа

Какая прямая называется перпендикулярной к плоскости?

Сформулируйте теорему о трёх перпендикулярах.

Найдите диагональ куба, ребро которого равно 1.

Вычислите угол между диагональю куба и диагональю плоскости основания.

Воспроизведение и коррекция опорных знаний

2.Определение.                                                                               

Углом между наклонной и плоскостью называется угол между наклонной и ее орто­гональной проекцией на эту плоскость.

III . Решение опорных задач

Назовите плоскости перпендикулярные ребру куба?

Доказательство. Докажем, что

При доказательстве перпендикулярности прямой и плоскости,

как правило, используется теорема о трех перпендикулярах.

IV. III . Решение задач по готовым чертежам

В кубе A…D1 найдите угол между прямой и плоскостью

AA1 и AB1C1.

В кубе A…D1 найдите угол между прямой и плоскостью

AA1 и BC1D.

В кубе A…D1 найдите угол между прямой и плоскостью

AB1 и BCC1.

В кубе A…D1 найдите угол между прямой и плоскостью

AB1 и ABC1.

В кубе A…D1 найдите угол между прямой и плоскостью

AB1 и BC1D.

В кубе A…D1 найдите угол между прямой и плоскостью

AB1 и BB1D1.

В кубе A…D1 найдите угол между прямой и плоскостью

AC1 и BCC1.

В кубе A…D1 найдите угол между прямой и плоскостью

AC1 и BB1D1.

В кубе A…D1 найдите угол между прямой и плоскостью

AC1 и BA1D.

 V . Решение задач типовых вариантов реальных заданий ЕГЭ 2013 математика, используя различные методы решения.

 Векторно-координатный метод решения  задач.

Вектор N _┴ β,  угол α, угол между

прямой  l и плоскостью β.

Устный диктант.

Назвать общее уравнение плоскости. (Ax + By + Cz + D = 0?

Геометрический  смысл коэффициентов общего уравнения плоскости?

( N(A,B,C)  перпендикулярен плоскости.)

Задача  1.  (С2.10. стр.74 «Универсальные материалы для подготовки учащихся  к ЕГЭ»  математика 2010.)

В кубе  A…D1  точка  Е - середина ребра   A ₁B ₁.                                                  

Найдите синус угла между прямой АЕ  и  плоскостью B D D₁.  А₁

Задача 2.  (самостоятельное решение) С 2 из варианта №1 типовых вариантов заданий ЕГЭ 2010 математика.

В кубе  A…D1  найдите угол между прямой   A B ₁ и плоскостью A BС _1.

Домашнее  задание  (карточки с разно уровневыми задачами, которые нужно решить различными методами: координатно-векторным методом,   методом дополнительных построений и геометрическим).

Карточки с домашнем заданием.

Уровень А.

В кубе  A…D1  найдите угол между прямой   СD ₁ и плоскостью ADD _1.

Уровень В.

В кубе A-D₁ найдите угол между прямой AС и плоскостью BCD_1.

В правильной шестиугольной призме A-F₁ все ребра которой равны 1, найдите угол между  прямой AB и  BCC₁ плоскостью BCC₁.

Уровень С.

В кубе A…D₁- найдите косинус угла между прямой DB ₁ и плоскостью ADD₁.

Весь материал - в документе.

Введение

Основным направлением модернизации школьного образования является отработка механизмов итоговой аттестации через введение единого государственного экзамена. В типовых вариантах реальных заданий ЕГЭ 2013 математика, задания С2 и С4 - геометрические задачи. Возникает вопрос: как подготовить учащихся к экзамену и научить решать задачи?

Казалось бы, для этого нужно решать задачи, предлагавшиеся на экзаменах в прошлые годы. Однако, если следовать только этому рецепту, то результат может оказаться вовсе не тем, который ожидается.

В каждом новом году экзаменационные задачи отличаются от задач прошлых лет, и из того, что узнали, как решаются задачи, предлагавшиеся на экзаменах в прошлые годы, не следует, что возможно решить другие задачи.

Важно, чтобы задачи, которые решаем, готовясь к экзамену, носили развивающий, системный характер, создавали базу для решения других задач.

Основные трудности решения задач по стереометрии связаны не столько с недостатками, вызванными незнанием формул и теорем или неумением их применять, сколько с недостаточно развитыми пространственными представлениями, неумением правильно изобразить пространственную ситуацию, установить взаимное расположение точек, прямых и плоскостей, указанных в задаче.

На уроке рассматривала задачи на нахождение углов между прямой и плоскостью и плоскостями. Они не только развивают пространственные представления, но и лежат в основе решения многих других задач на вычисление площадей и объемов пространственных фигур, позволяют сформировать и отработать необходимые навыки решения этих задач. От того, как обучающиеся научатся решать эти базовые задачи, овладеют различными методами решения геометрических задач, во многом зависит успешность решения многих других задач.

Большую пользу для развития пространственных представлений оказывают размышления над задачей, анализ ее условия, выяснение взаимного расположения точек, прямых и плоскостей, указанных в условии задачи, и даже просто исследование чертежа.

На повторение темы «Угол между прямой и плоскостью. Угол между плоскостями», отводится 2 часа.

Урок по математике

Учитель. Назарова Л.В. Школа: МОУ СОШ п. Индустриальный Екатериновского района

Предмет: геометрия.

Учебный план – 6 часов в неделю (из них 4часа – алгебра и начала анализа, 2 часа геометрия).

Класс 11.

Тема: «Угол между прямой и плоскостью».

Тип урока: повторение, обобщение и систематизация знаний.

Цели урока:

Образовательная: обобщить, систематизировать знания учащихся об углах между прямой и плоскостью; продолжить формирование умений и навыков в в решении задач по данной теме.

Развивающая: углубление знаний, умений и навыков, знакомство с различными методами (геометрическим, векторно-координатнм, методом дополнительных построений); развитие творческой деятельности: интуиции, пространственного воображения, смекалки.

Воспитательная: приучать к эстетическому оформлению записи в тетради, прививать аккуратность и трудолюбие.

1. Устная работа

2. Какая прямая называется перпендикулярной к плоскости?

3. Сформулируйте теорему о трёх перпендикулярах.

4. Найдите диагональ куба, ребро которого равно 1.

5. Вычислите угол между диагональю куба и диагональю плоскости основания.

Воспроизведение и коррекция опорных знаний

2.Определение.

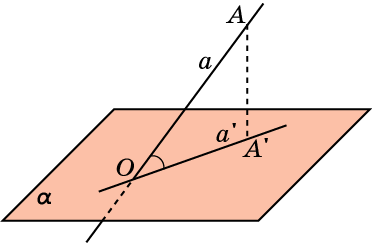Углом между наклонной и плоскостью называется угол между наклонной и ее орто­гональной проекцией на эту плоскость.

III . Решение опорных задач

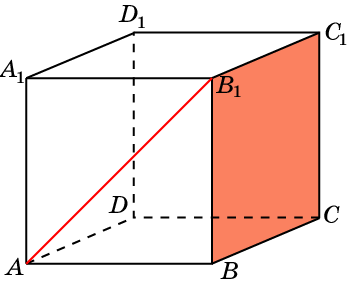
1. Назовите плоскости перпендикулярные ребру куба?

(AD DD₁C₁C, AD 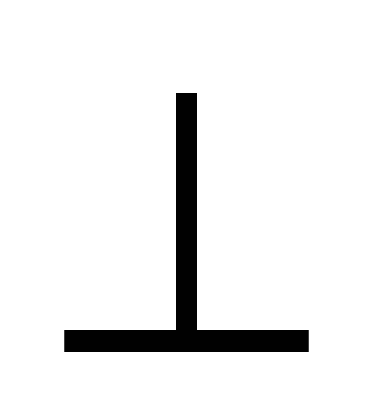ABB₁A₁₎

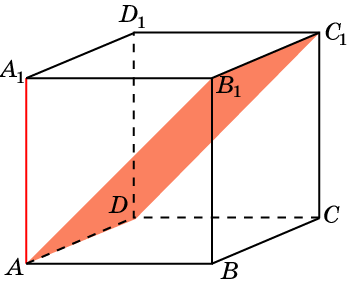
1. Докажите, что A₁C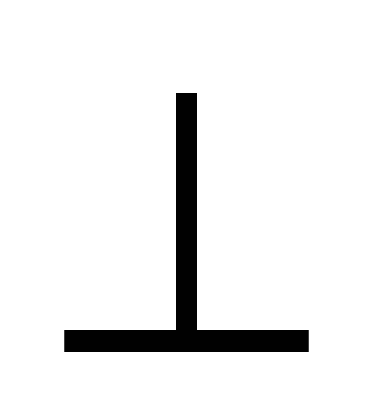 B₁D₁A

Доказательство. Докажем, что

а)A₁C 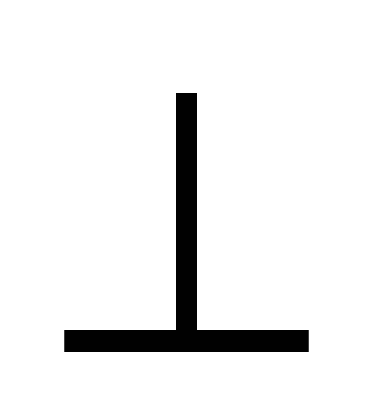AD₁

б)A₁C 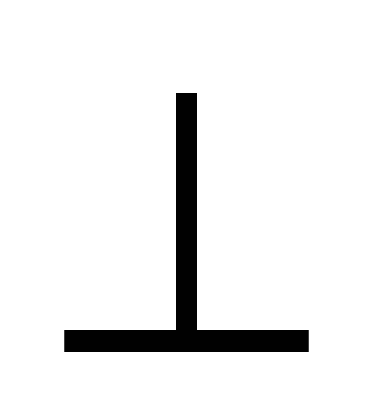B₁D₁

При доказательстве перпендикулярности прямой и плоскости,

как правило, используется теорема о трех перпендикулярах.

а)Спроектируем A₁C на плоскость AD₁D. Пр A₁C= A₁D, т.к.

A₁D AD₁ = A₁C AD₁

б)Докажем, что A₁C B₁D_{1 :} β= (A₁B₁C₁D₁) Пр _β A₁C= A₁C_1, т.к.

A₁C₁ B₁D₁ = A₁C B₁D₁

IV. III . Решение задач по готовым чертежам

В кубе A…D1 найдите угол между прямой и плоскостью

AA1 и AB1C1.

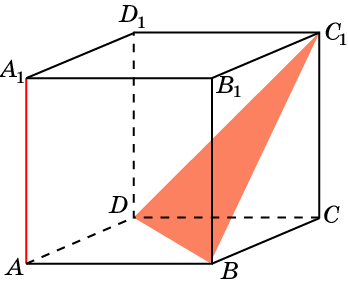В кубе A…D1 найдите угол между прямой и плоскостью

AA1 и BC1D.

В кубе A…D1 найдите угол между прямой и плоскостью

AB1 и BCC1.

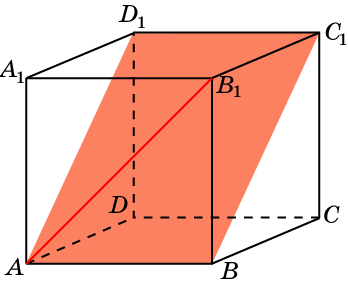В кубе A…D1 найдите угол между прямой и плоскостью

AB1 и ABC1.

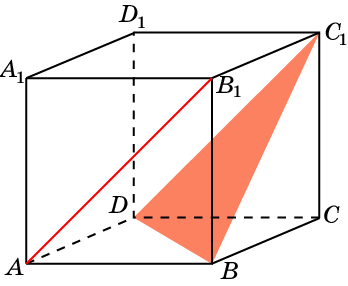В кубе A…D1 найдите угол между прямой и плоскостью

AB1 и BC1D.

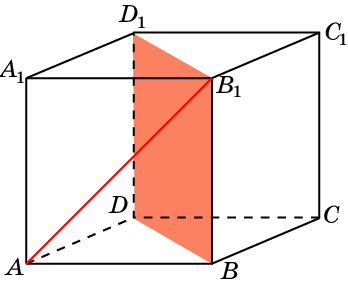В кубе A…D1 найдите угол между прямой и плоскостью

AB1 и BB1D1.

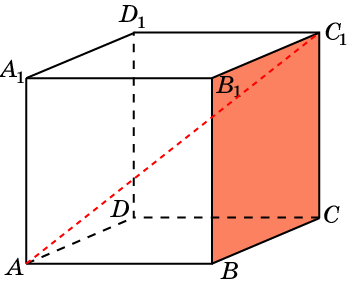В кубе A…D1 найдите угол между прямой и плоскостью

AC1 и BCC1.

В кубе A…D1 найдите угол между прямой и плоскостью

AC1 и BB1D1.

В кубе A…D1 найдите угол между прямой и плоскостью

AC1 и BA1D.

V . Решение задач типовых вариантов реальных заданий ЕГЭ 2013 математика, используя различные методы решения.

1. Векторно-координатный метод решения задач.

Вектор N _┴ β, угол α, угол между

прямой l и плоскостью β.

N a cos (N ,a) = cos (90 - α) = sin α

α

β

l sin α = (1)

Устный диктант.

1. Назвать общее уравнение плоскости. (Ax + By + Cz + D = 0?

2. Геометрический смысл коэффициентов общего уравнения плоскости?

( N(A,B,C) перпендикулярен плоскости.)

1. Пусть вектор N _┴ β, вектор а || l . найдите угол между прямой и плоскостью. (α = 90 - (N ,a) = sin α =

Задача 1. (С2.10. стр.74 «Универсальные материалы для подготовки учащихся к ЕГЭ» математика 2010.)

В кубе A…D1 точка Е - середина ребра A ₁B ₁. D₁ С₁

Найдите синус угла между прямой АЕ и плоскостью B D D₁. А₁

Решение.

Вектор _ перпендикулярен плоскости С

(ВВ ₁ D₁), вектор _ || прямой АЕ. А В

а – угол между прямой АЕ и плоскостью (ВВ ₁ D₁₎.

_ = _

Если есть три взаимно перпендикулярных ребра, то можно ввести систему координат.

_||оси OX

_|| оси OY

_|| оси ОZ

точка D(0;0;0) обозначим |DD₁| =Z 0

По нашему выбору координат точка А(1;0;0), Е(1;1/2;1), А₁(1;0;1), С₁(0;1;1)

_ {0;1/2;1} _|= _ =_{ } ;

_{-1;1;0} _|=_=_ .

_=_

Ответ: _

Задача 2. (самостоятельное решение) С 2 из варианта №1 типовых вариантов заданий ЕГЭ 2010 математика.

В кубе A…D1 найдите угол между прямой A B ₁ и плоскостью A BС _1.

Решение. D₁ С₁

Вектор CD ₁ перпендикулярен плоскости (АВС₁ ),

вектор АВ₁ || прямой АВ₁ , А₁

α – угол между прямой АВ₁ и плоскостью (АВС₁ ).

Для нахождения угла α используем формулу (1). D ₁ С

Запишем её для наших векторов. А В

Чтобы найти координаты векторов и их абсолютные величины, введём систему координат.

Пусть _||оси OX

_|| оси OY

_|| оси ОZ

Точка D(0;0;0) обозначим |DD₁| =Z 0, по нашему выбору координат точка А(1;0;0), С(0;1;0), В₁(1;1;1).

_{0;1;1}, _=_=_

_{1;0;1}, _= _=_,

_=_ , _. Ответ: 30 ⁰.

Домашнее задание (карточки с разно уровневыми задачами, которые нужно решить различными методами: координатно-векторным методом, методом дополнительных построений и геометрическим).

Карточки с домашнем заданием.

Уровень А.

В кубе A…D1 найдите угол между прямой СD ₁ и плоскостью ADD _1.

Уровень В.

1. В кубе A-D₁ найдите угол между прямой AС и плоскостью BCD_1.

2. В правильной шестиугольной призме A-F₁ все ребра которой равны 1, найдите угол между прямой AB и BCC₁ плоскостью BCC₁.

Уровень С.

1. В кубе A…D₁- найдите косинус угла между прямой DB ₁ и плоскостью ADD₁.