Нахождение угла между скрещивающимися прямыми
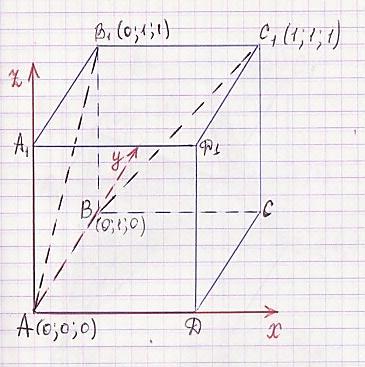
Задание: В единичном кубе ABCDA1B1C1D1 найдите угол между прямыми AB1 и ВC1 Найти направляющие векторы прямых.
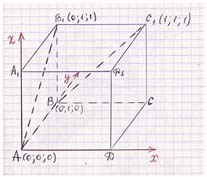
Найти косинус угла по формуле.
Задачи для самостоятельного решения:
1. Сторона основания правильной четырехугольной призмы ABCDA1B1C1D1 равна 2, высота – 4. Точка Е - середина отрезка CD, точка F –середина отрезка АD. Найти угол между прямыми CF и B1E
2. Точка О лежит на ребре DD1 куба ABCDA1B1C1D1, точка Р является точкой пересечения диагоналей грани ABCD. DO:DD1=1:5. Найдите косинус угла между прямой ОР и прямой, содержащей диагональ куба, выходящую из вершины С.
Нахождение угла между плоскостями (Чертеж смотрите в документе)
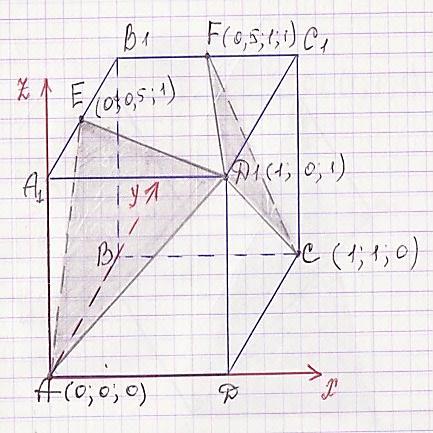
Задание: В единичном кубе ABCDA1B1C1D1 найдите угол между плоскостями (AD1E) и (D1FC), где Е и Fсередины ребер A1B1 и В1C1 соответственно
Составить уравнения плоскостей
Найти координаты векторов нормалей к плоскостям
Найти косинус угла между векторами нормалей
Задачи для самостоятельного решения:
1. В правильной треугольной призме ABCA1B1C1, ребра которой равны 1, найдите косинус угла между плоскостями (ACB1) и (BA1C1)
2. В правильной четырехугольной призме ABCDA1B1C1D1 стороны основания равны 1, а боковые ребра равны 5. На ребре АА1 отмечена точка Е так, что АЕ:ЕА1=2:3. Найдите косинус угла между плоскостями АВС и ВЕD1
Нахождение угла между прямой и плоскостью (Чертеж смотрите в документе)
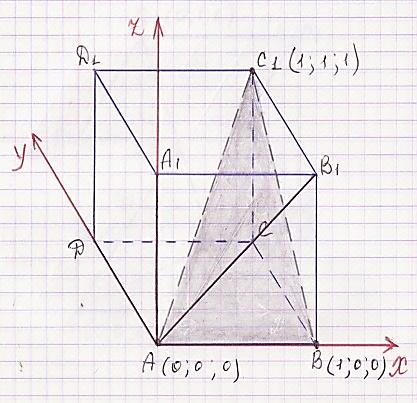
Задание: В единичном кубе ABCDA1B1C1D1 найдите угол между плоскостью (АВС1) и прямой АВ1
Составить уравнение плоскости
Найти координаты вектора нормали к плоскости
Найти координаты направляющего вектора прямой
Воспользоваться формулой (Смотрите документ)
Задачи для самостоятельного решения:
1. В прямоугольном параллелепипеде ABCDA1B1C1D1 ребра АВ и АА1 равны 1, а ребро АD=2. Точка Е – середина ребра В1С1. Найдите угол между прямой ВЕ и плоскостью (АВ1С)
2. В правильной четырехугольной пирамиде ABCDS, все ребра которой равны 1, найдите синус угла между прямой ВЕ и плоскостью (SAD) , где Е – середина ребра SC
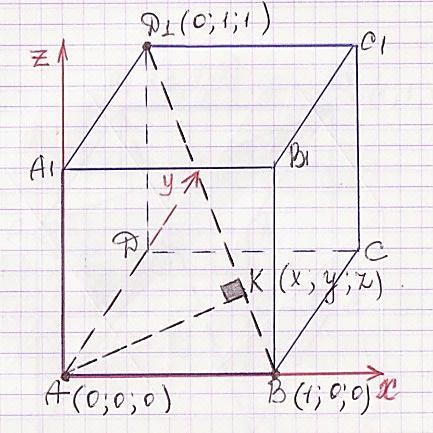
Нахождение расстояния от точки до прямой (Чертеж смотрите в документе)
Задание: В единичном кубе ABCDA1B1C1D1 найдите расстояние от точки А до прямой ВD1 (Смотрите документ)
Задачи для самостоятельного решения:
В правильной шестиугольной пирамиде ABCDEFS , стороны основания которой равны 1, а боковые ребра равны 2, найти расстояние от точки F до прямой BG, где G – середина ребра SC
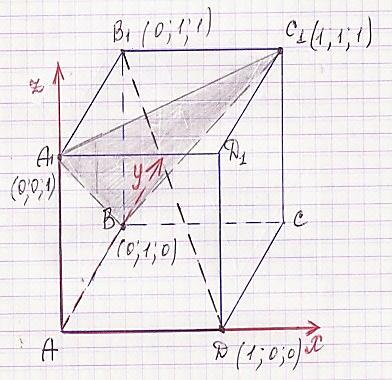
Нахождение расстояния от точки до плоскости (Чертеж смотрите в документе)
Задание: В единичном кубе ABCDA1B1C1D1 проведена диагональ B1D. В каком отношении, считая от вершины В1, плоскость А1ВС1 делит диагональ В1D
Составить уравнение плоскости
Найти координаты вектора нормали к плоскости
Воспользоваться формулой (смотрите в документе)
Задачи для самостоятельного решения:
1. В единичном кубе ABCDA1B1C1D1 найдите расстояние от точки А до плоскости (ВDА1)
(Полную версию разработки смотрите в документе)

 Получите свидетельство
Получите свидетельство Вход
Вход


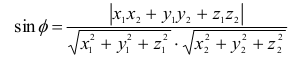

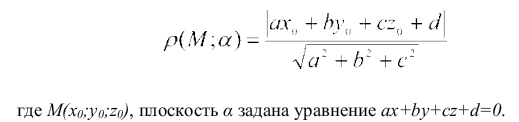









 Метод координат в пространстве для школьников (0.44 MB)
Метод координат в пространстве для школьников (0.44 MB)
 0
0 3084
3084 192
192 Нравится
0
Нравится
0



