Тема урока: "Теорема ..." (теорема Виета)

Урок по теме :

«Теорема …»

«Учение без размышления бесполезно»

Конфуций

«Все математики знали, что под их алгеброй были скрыты несравненные сокровища, но не умели их найти; задачи, которые они считали наиболее трудными, легко решаются десятками с помощью нашего искусства.»

Кроссворд

4

2

1

3

К

О

Э

Ф

Ф

И

Ц

И

Е

Н

Т

Ы

По вертикали:

1. Квадратное уравнение с первым коэффициентом равным 1.

2. От чего зависит количество корней квадратного уравнения?

3. Один из видов квадратного уравнения.

4. Как называются буквы а, b, c входящие в запись общего вида квадратного уравнения?

По горизонтали:

5. Фамилия автора теоремы.

Д

И

С

К

Р

И

М

И

Н

А

Н

Т

П

Р

И

В

Е

Д

Е

Н

Н

О

Е

Н

Е

П

О

Л

Н

О

Е

5

Цель урока:

открытие теоремы Виета.

Франсуа Виет

Французский математик конца 16 века, один из тех, кто внес большой вклад в развитие математики.

Альма-матер Виета - университет Пуатье

*** А́льма - ма́тер  — старинное неформальное название учебных заведений (университетов, которые изначально давали в основном теологическое и философское образование), как организаций, питающих духовно.

Адвокатская деятельность

Генрих IV

Генрих III

В конце 16 столетия голландский математик Андриан ван-Роумен, решил бросить вызов всем математикам мира. Он разослал во все европейские страны уравнение 45-й степени:

x 45 –45x 43 +945x 41 –12300x 39 +……+9563x 5 –3795x 3 +45x=a

Способы решения квадратных уравнений:

• - выделение квадрата двучлена;
• - по формуле корней;

• - графический;
• - с помощью теоремы Виета.

Результат трудов Виета:

Новая система математического языка позволила просто, ясно и компактно описать общие законы арифметики и алгоритмы. Символика Виета была сразу же оценена учёными разных стран, которые приступили к её совершенствованию.

Квадратным уравнением называется уравнение вида:

Обозначив

получим

- приведённое квадратное уравнение

Задание

№

Уравнение

I

II

III

3

2

6

5

-3

-4

-7

12

-5

3

-2

-15

Гипотеза

Сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.

Познакомили поэта С теоремою Виета. Оба корня он сложил, минус p он получил, а корней произведенье дает q из уравнения .

Проблемная задача

В уравнении х 2 + рх + q = 0 корнями являются числа 5 и -8.

Найдите коэффициенты квадратного уравнения.

х 2 + 3х -40 = 0

работа с учебником

• Стр. 173 № 29.6

• Стр. 173 № 29.9

ФИЗКУЛЬТМИНУТКА

Теорема Виета

Если приведенное квадратное уравнение

имеет два корня, то сумма его корней равна коэффициенту при х , взятому с противоположным знаком ( p ), произведение корней равно свободному члену ( q ).

Обратная теорема:

Если два числа таковы, что их сумма равна второму коэффициенту с противоположным знаком, а произведение свободному члену, то эти числа являются корнями квадратного уравнения.

Эти теоремы удобно применять для:

• нахождения корней подбором:

• проверки правильности корней:

• составления квадратных уравнений по известным корням.

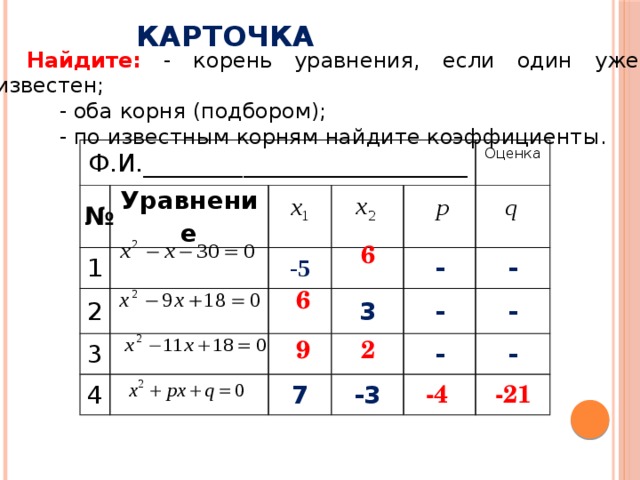
Карточка

Найдите: - корень уравнения, если один уже известен;

- оба корня (подбором);

- по известным корням найдите коэффициенты.

Ф.И.__________________________

№

Уравнение

1

2

-5

3

Оценка

4

3

-

-

-

7

-3

-

-

-

6

6

2

9

-21

-4

Подведение итогов:

«Теорема Виета»

«Учение без размышления бесполезно»

Конфуций

Цель урока:

открытие «теоремы Виета».

Домашнее задание

• Стр.168, теоремы;
• карточки.

Спасибо за урок!