Тест по математике "Сфера, шар"

Тест можно применить не только в школах, но и в СПО. А также можно использовать не только на уроках, но и на дополнительных занятиях для усовершенствования уровня знаний обучающихся по теме "Сфера, шар". В данном тесте имеются критерии оценивания, что облегчает проверку теста учителем и объясняет какую оценку получил обучающийся.

1. Выберите верное утверждение:

A. Сфера -  поверхность, состоящая из точки пространства, расположенной в центре.

B. Сфера -  поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии от данной точки.

C. Сфера -  многогранник, состоящий из всех точек пространства, расположенных на данном расстоянии от данной точки.

2. Выберите верное утверждение:

A. Шар -  отрезок, ограниченный сферой.

B. Шар -  тело, ограниченное многоугольником

C. Шар -  тело, ограниченное сферой.

Тест по теме «Сфера, шар»

Критерии оценивания:

10 верных ответов – «5»

8 верных ответов – «4»

6 верных ответов – «3»

1. Выберите верное утверждение:

• Сфера -  поверхность, состоящая из точки пространства, расположенной в центре.
• Сфера -  поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии от данной точки.
• Сфера -  многогранник, состоящий из всех точек пространства, расположенных на данном расстоянии от данной точки .

2. Выберите верное утверждение:

• Шар -  отрезок, ограниченный сферой.
• Шар -  тело, ограниченное многоугольником
• Шар -  тело, ограниченное сферой

3. Установите соответствие:

Условие:

Вывод :

1. Если расстояние от центра сферы до плоскости меньше радиуса сферы

А то сфера и плоскость имеют только одну общую точку

2. Если расстояние от центра сферы до плоскости равно радиусу сферы

В то сфера и плоскость не имеют общих точек.

3. Если расстояние от центра сферы до плоскости больше радиуса сферы

С то сечение сферы плоскостью есть круг.

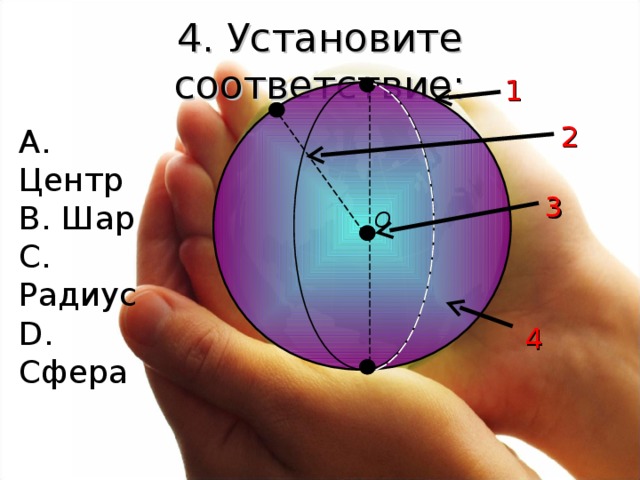
4. Установите соответствие:

1

2

А. Центр

В. Шар

С. Радиус

D . Сфера

3

О

4

5. Выберите формулу уравнения сферы :

• (х-х 0 ) 2 +(у+у 0 ) 2 +(z- z 0 ) 2 = R 2 .
• (х-х 0 ) +(у - у 0 ) 2 +(z- z 0 ) 2 = R 2
• (х-х 0 ) 2 +(у - у 0 ) 2 +(z- z 0 ) 2 = R 2

Проверка

1. Выберите верное утверждение:

• Сфера -  поверхность, состоящая из точки пространства, расположенной в центре.
• Сфера -  поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии от данной точки.
• Сфера -  многогранник, состоящий из всех точек пространства, расположенных на данном расстоянии от данной точки .

2. Выберите верное утверждение:

• Шар -  отрезок, ограниченный сферой.
• Шар -  тело, ограниченное многоугольником
• Шар -  тело, ограниченное сферой

3. Установите соответствие:

Условие:

Вывод :

1. Если расстояние от центра сферы до плоскости меньше радиуса сферы

А то сфера и плоскость имеют только одну общую точку

2. Если расстояние от центра сферы до плоскости равно радиусу сферы

В то сфера и плоскость не имеют общих точек.

3. Если расстояние от центра сферы до плоскости больше радиуса сферы

С то сечение сферы плоскостью есть круг.

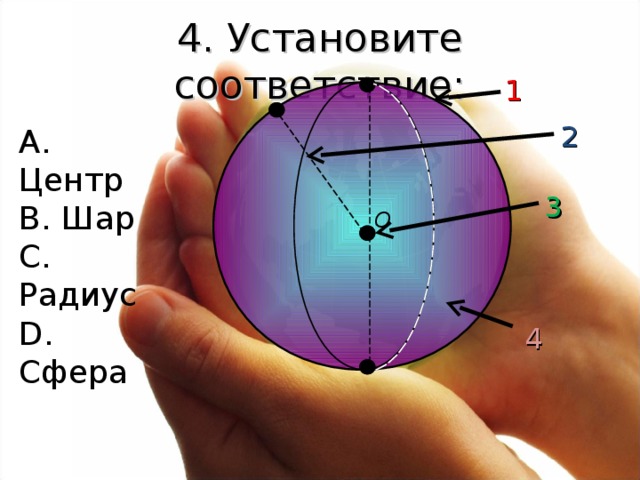
4. Установите соответствие:

1

2

А. Центр

В. Шар

С. Радиус

D . Сфера

3

О

4

5. Выберите формулу уравнения сферы :

• (х-х 0 ) 2 +(у+у 0 ) 2 +(z- z 0 ) 2 = R 2 .
• (х-х 0 ) +(у - у 0 ) 2 +(z- z 0 ) 2 = R 2
• (х+х 0 ) 2 +(у - у 0 ) 2 +(z- z 0 ) 2 = R 2

Ответы

• B
• C
• 1-C, 2-A, 3- B
• 1-D, 2-C, 3- A, 4-B
• В