Содержание
1.Пояснительная записка…………………………………………………………………………………………2-3
Содержание тем учебного курса…………………………………………………………………………………4-5
Тематическое планирование учебного материала ……………………………………………………………6-10
Требования к уровню подготовки обучающихся……………………………………………………………..11-12
Переченьучебно-методического обеспечения рабочей программы……………………………………………13
Список литературы……………………………………………………………………………………………….14-15
Пояснительная записка
Настоящая рабочая программа составлена на основе авторской программы Л.С. Атанасяна, В.Ф. Бутузова, С.Б. Кадомцева и др., входящей в учебное издание «Программы общеобразовательных учреждений. Геометрия. 10-11 классы.». сост.: Бурмистрова Т.А. -М.: «Просвещение», 2013г., в соответствии с требованиями федерального компонента Государственного образовательного стандарта среднего (полного) общего образования по математике, предъявляемыми к профильному уровню обучения.
Программа ориентирована на учащихся 11 классов для базового изучения геометрии, разработана к учебнику: Атанасяна Л.С. и др. «Геометрия 10-11».
Геометрия — один из важнейших компонентов математического образования, необходимый для приобретения конкретных знаний о пространстве и практически значимых умений, формирования языка описания объектов окружающего мира, для развития пространственного воображения и интуиции, математической культуры, для эстетического воспитания учащихся. Изучение геометрии вносит вклад в развитие логического мышления, в формирование понятия доказательства.
В данном курсе представлены следующие содержательные линии: «Векторы в пространстве», «Метод
координат в пространстве», «Цилиндр, конус, шар», «Объемы тел».
В рамках указанных содержательных линий решаются следующие задачи:
• формирование практических навыков выполнения устных, письменных, инструментальных вычислений, развитие вычислительной культуры;
• развитие пространственных представлений и изобразительных умений, освоение основных фактов и методов стереометрии ;
• развитие логического мышления и речи — умения логически обосновывать суждения, проводить несложные систематизации, доказательные рассуждения, использовать различные языки математики (словесный, символический, графический) для иллюстрации, интерпретации, аргументации и доказательства;
Изучение геометрии на базовом уровне направлено на достижение следующих целей:
формирование представлений об идеях и методах математики; о математике как универсальном языке науки, средстве моделирования явлений и процессов;
овладение устным и письменным математическим языком, математическими знаниями и умениями, необходимыми для изучения школьных естественно-научных дисциплин, для продолжения образования и освоения избранной специальности на современном уровне;
развитие логического мышления, алгоритмической культуры, пространственного воображения, развитие математического мышления и интуиции, творческих способностей на уровне, необходимом для продолжения образования и для самостоятельной деятельности в области математики и ее приложений в будущей профессиональной деятельности;
воспитание средствами математики культуры личности через знакомство с историей развития математики, эволюцией математических идей; понимания значимости математики для общественного прогресса.
В учебный комплект входят: «Геометрия, 10- 11» авт. Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др. – учебник для общеобразоват. учреждений - М. : Просвещение, 2007; дидактические материалы по геометрии для 11 классов авт. Б.Г. Зив.
Выполнение практической части представлено 6 контрольными работами (контрольные работы рассчитаны на один урок), 2 тестами и 3 самостоятельными работами.
Место предмета в базисном учебном плане
Согласно федеральному базисному учебному плану для образовательных учреждений Российской Федерации на обязательное изучение геометрии на этапе общего среднего образования для профильного изучения в 11 классе отводится 68 часов ( 2 часа в неделю ).
Содержание тем учебного курса
1. Векторы в пространстве
Понятие вектора в пространстве. Сложение и вычитание векторов. Умножение вектора на число. Компланарные векторы.
Основная цель — закрепить известные учащимся из курса планиметрии сведения о векторах и действиях над ними, ввести понятие компланарных векторов в пространстве и рассмотреть вопрос о разложении любого вектора по трем данным некомпланарным векторам.
2. Метод координат в пространстве. Движения
Координаты точки и координаты вектора. Скалярное произведение векторов. Уравнение плоскости. Движения. Преобразование подобия.
Основная цель — сформировать умение учащихся применять векторно — координатный метод к решению задач на вычисление углов между прямыми и плоскостями и расстояний между двумя точками, от точки до плоскости.
3. Цилиндр, конус, шар
Понятие цилиндра. Площадь поверхности цилиндра. Понятие конуса. Площадь поверхности конуса. Усеченный конус. Сфера и шар. Уравнение сферы. Взаимное расположение сферы и плоскости. Касательная плоскость к сфере. Площадь сферы.
Основная цель — дать учащимся систематические сведения об основных телах и поверхностях вращения - цилиндре, конусе, сфере, шаре.
В данном разделе изложены также вопросы о взаимном расположении сферы и прямой, о сечениях цилиндрической и конической поверхностей различными плоскостями.
4. Объемы тел
Объем прямоугольного параллелепипеда. Объемы прямоугольной призмы и цилиндра. Объемы наклонной призмы, пирамиды и конуса. Объем шара и площадь сферы. Объемы шарового сегмента, шарового слоя и шарового сектора.
Основная цель — ввести понятие объема тела и вывести формулы для вычисления объемов основных многогранников и круглых тел, изученных в курсе стереометрии.
5. Некоторые сведения из планиметрии
Углы и отрезки, связанные с окружностью. Эллипс, гипербола и парабола.
Основная цель — расширить известные учащимся сведения о геометрических фигурах на плоскости: рассмотреть ряд теорем об углах и отрезках, связанных с окружностью, познакомить учащихся с такими интересными объектами, как окружность и прямая Эйлера, дать геометрические определения эллипса, гиперболы, параболы и вывести их канонические уравнения.
Изучение этих теорем и формул целесообразно совместить с рассмотрением тех или иных вопросов стереометрии:
- теоремы об углах и отрезках, связанных с окружностью, рассмотреть при изучении темы «Сфера и шар»;
- сведения об эллипсе, гиперболе и параболе использовать при рассмотрении сечений цилиндрической и конической поверхностей.
6. Обобщающее повторение
Тематическое планирование учебного материала
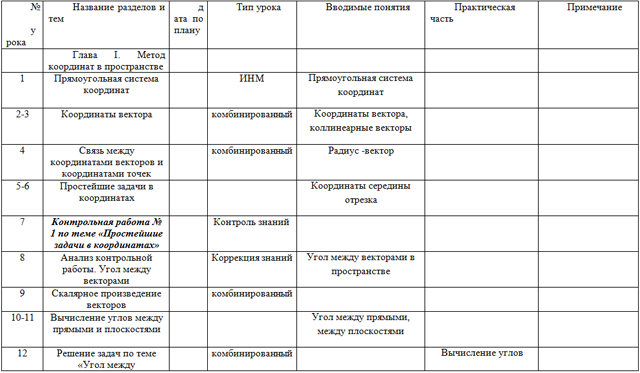
| № урока | Название разделов и тем | дата по плану | Тип урока | Вводимые понятия | Практическая часть | Примечание |
|
| Глава I. Метод координат в пространстве |
|
|
|
|
|
| 1 | Прямоугольная система координат |
| ИНМ | Прямоугольная система координат |
|
|
| 2-3 | Координаты вектора |
| комбинированный | Координаты вектора, коллинеарные векторы |
|
|
| 4 | Связь между координатами векторов и координатами точек |
| комбинированный | Радиус -вектор |
|
|
| 5-6 | Простейшие задачи в координатах |
|
| Координаты середины отрезка |
|
|
| 7 | Контрольная работа № 1 по теме «Простейшие задачи в координатах» |
| Контроль знаний |
|
|
|
| 8 | Анализ контрольной работы. Угол между векторами |
| Коррекция знаний | Угол между векторами в пространстве |
|
|
| 9 | Скалярное произведение векторов |
| комбинированный |
|
|
|
| 10-11 | Вычисление углов между прямыми и плоскостями |
|
| Угол между прямыми, между плоскостями |
|
|
| 12 | Решение задач по теме «Угол между прямыми и плоскостями» |
| комбинированный |
| Вычисление углов между векторами |
|
| 13 | Движения |
| комбинированный | Понятие движения, симметрии,, поворота, параллельного переноса |
|
|
| 14-15 | Обобщение по теме «Метод координат в пространстве» |
| обобщающий |
|
|
|
| 16 | Контрольная работа №2 по теме «Метод координат в пространстве» |
| Контроль знаний |
|
|
|
|
| Глава II. Цилиндр, конус, шар |
|
|
|
|
|
| 17 | Анализ контрольной работы. Понятие цилиндра |
| Коррекция знаний | Цилиндр и его элементы |
|
|
| 18-19 | Площадь поверхности цилиндра |
| ИНМ | Площадь поверхности |
|
|
| 20 | Решение задач по теме «Цилиндр» |
| комбинированный |
| Вычисление элементов цилиндра |
|
| 21 | Понятие конуса |
| комбинированный | Конус и его элементы |
|
|
| 22-23 | Площадь поверхности конуса |
| комбинированный | Поверхность конуса |
|
|
| 24-25 | Усеченный конус |
| комбинированный | Усеченный конус и его элементы |
|
|
| 26 | Сфера и шар |
| комбинированный | Шар, сфера |
|
|
| 27 | Уравнение сферы |
| комбинированный |
|
|
|
| 28-29 | Касательная плоскость к сфере |
| комбинированный | Плоскость касательная к сфере |
|
|
| 30 | Площадь сферы |
| комбинированный | Площадь поверхности сферы |
|
|
| 31-33 | Разные задачи на многогранники, цилиндр, конус и шар |
| комбинированный |
| Вычисление элементов сферы и шара |
|
| 34-35 | Обобщение по теме «Цилиндр, конус, шар» |
| обобщающий |
| Вычисление элементов цилиндра, конуса и шара |
|
| 36 | Контрольная работа №3 по теме «Цилиндр, конус, шар» |
| Контроль знаний |
|
|
|
|
| Глава III. Объёмы тел |
|
|
|
|
|
| 37 | Анализ контрольной работы. Понятие объема |
| Коррекция знаний | Понятие объема, единицы объема |
|
|
| 38-39 | Объем прямоугольного параллелепипеда |
| комбинированный | Объем прямоугольного параллелепипеда |
|
|
| 40 | Объем прямой призмы |
| комбинированный | Объем прямой призмы |
|
|
| 41 | Объем цилиндра |
| комбинированный | Объем цилиндра |
|
|
| 42 | Решение задач по теме «Объемы тел» |
| комбинированный |
| Вычисление объема тел |
|
| 43 | Вычисление объемов тел с помощью определенного интеграла |
|
|
|
|
|
| 44 | Объем наклонной призмы |
| комбинированный | Объем наклонной призмы |
|
|
| 45-46 | Объем пирамиды |
|
| Объем пирамиды |
|
| 47 | Решение задач по теме «Объем призмы и пирамиды» |
| комбинированный |
| Вычисление объемов призм и пирамид |
|
| 48-49 | Объем конуса |
|
| Объем конуса |
|
|
| 50 | Обобщение по теме «Объемы тел» |
| комбинированный |
|
|
|
| 51 | Контрольная работа №4 по теме «Объемы тел» |
| Контроль знаний |
|
|
|
| 52 | Анализ контрольной работы. Решение задач (ЕГЭ) |
| Коррекция знаний |
|
|
|
| 53-54 | Объем шара |
|
| Объем шара |
|
|
| 55-57 | Объем шарового сегмента, шарового слоя, шарового сектора |
| комбинированный | Объем частей шара |
|
|
| 58 | Площадь сферы |
| комбинированный | Площадь поверхности шара |
|
|
| 59 | Обобщение по теме «Объем шара и площадь сферы» |
|
|
|
|
|
| 60 | Контрольная работа№5 по теме «Объем шара и площадь сферы» |
| Контроль знаний |
|
|
|
|
| Итоговое повторение |
| Повторение |
|
|
|
| 61-62 | Анализ контрольной работы. Задачи по планиметрии (В4) |
| комбинированный |
|
|
|
| 63-64 | Площадь многоугольника, площадь поверхности многогранника (В6, В9) |
| комбинированный |
|
|
|
| 65-66 | Задачи по стереометрии (С2) |
| комбинированный |
|
|
|
| 67-68 | Задачи, имеющие несколько решений (С4) |
| комбинированный |
|
|
|
Требования к уровню подготовки обучающихся
В результате изучения геометрии на профильном уровне ученик должен
знать/понимать
• возможности геометрии для описания свойств реальных предметов и их взаимного расположения;
• различие требований, предъявляемых к доказательствам в математике, естественных, социально-экономических и гуманитарных науках, на практике;
• роль аксиоматики в математике; возможность построения математических теорий на аксиоматич
основе; значение аксиоматики для других областей знания и для практики.
Уметь:
• соотносить плоские геометрические фигуры и трехмерные объекты с их описаниями, чертежами, изображениями; различать и анализировать взаимное расположение фигур;
• изображать геометрические фигуры и тела, выполнять чертеж по условию задачи;
• решать геометрические задачи, опираясь на изученные свойства планиметрических и стереометрических фигур и отношений между ними, применяя алгебраический и тригонометрический аппарат;
• проводить доказательные рассуждения при решении задач, доказывать основные теоремы курса;
• вычислять линейные элементы и углы в пространственных конфигурациях, объемы и площади поверхностей пространственных тел и их простейших комбинаций;
• применять координатно-векторный метод для вычисления отношений, расстояний и углов;
• строить сечения многогранников и изображать сечения тел вращения.
Перечень
учебно-методического обеспечения рабочей программы
Атанасян Л.С., Бутузов В.Ф. Геометрия в 10-11 класс. М.;
Зив. Б.Г., Мейлер В.М., Баханский А.Г. Задачи по геометрии для 7-11 классов. М., 2005;
Звавич Л.И. Контрольные и проверочные работы по геометрии 10-11 класс. М., 2001;
Изучение геометрии в 10 – 11 классах: Методические рекомендации к учебнику. Книга для учителя / С.М. Саакян, В.Ф. Бутузов. – М.: Просвещение, 2010
Геометрия. Дидактические материалы. 10 кл. / Зив. Б.Г. – М.: Просвещение, 2009
Список литературы
(основной и дополнительной)
для учителя:
В.И. Глизбург. Контрольные работы по курсу алгебры, 11 (под ред. А.Г. Мордковича);
Александрова. Самостоятельные работы по алгебре и началам анализа 11 класс;
Зив. Б.Г., Мейлер В.М., Баханский А.Г. Задачи по геометрии для 7-11 классов. М., 2005;
Звавич Л.И. Контрольные и проверочные работы по геометрии 10-11 класс. М., 2001;
А.Г. Мордкович Алгебра. 10-11.Методическое пособие для учителя
Единый государственный экзамен 2012. Математика. Учебно-тренировочные материалы для подготовки учащихся / ФИПИ авторы-составители: Ященко И.В., Семенов А.Л., Высоцкий И.Р., Гущин Д.Д., Захаров П.И., Панферов В.С., Посицельский С.Е., Семенов А.В., Семенова М.А., Сергеев И.Н., Смирнов В.А., Шестаков С.А., Шноль Д.Э. – М.: Интеллект-Центр, 2010.
ЕГЭ-2012: Математика / ФИПИ авторы-составители: Ященко И.В., Семенов А.Л., Высоцкий И.Р., Гущин Д.Д., Захаров П.И., Панферов В.С., Посицельский С.Е., Семенов А.В., Семенова М.А., Сергеев И.Н., Смирнов В.А., Шестаков С.А., Шноль Д.Э.– М.: Астрель, 2010.
Математика. Еженедельное приложение к газете «Первое сентября».
Математика в школе. Ежемесячный научно-методический журнал.
Интернет – ресурсы:
– Министерство образования РФ: http://www.informika.ru/;; http://www.ege.edu.ru/
– Тестирование online: 5 - 11 классы : http://www.kokch.kts.ru/cdo/
– Педагогическая мастерская, уроки в Интернет и многое другое: http://teacher.fio.ru
– Новые технологии в образовании: http://edu.secna.ru/main/
– Мегаэнциклопедия Кирилла и Мефодия: http://mega.km.ru
– сайты «Энциклопедий»: http://www.rubricon.ru/ ; http://www.encyclopedia.ru/
для учащихся:
Математика. Тренировочные тематические задания повышенной сложности с ответами для подготовки к ЕГЭ и к другим формам выпускного и вступительного экзаменов / сост. Г.И. Ковалева, Т.И. Бузулина, О.Л. Безрукова, Ю.А. Розка –Волгоград: Учитель,2009г.
Сборники для подготовки и проведения ЕГЭ / 2006- 2011гг.
С.М.Саакян, А.М.Гольдман, Д.В.Денисов. Задачи по алгебре и началам анализа. - М: Просвещение
Зив Б.Г. Дидактические материалы по геометрии, 11 класс, М., 2005.
Страница 25 из 25

 Получите свидетельство
Получите свидетельство Вход
Вход











 Рабочая программа по геометрии (11-е классы) (33.41 КB)
Рабочая программа по геометрии (11-е классы) (33.41 КB)
 0
0 807
807 151
151 Нравится
0
Нравится
0




