Рабочая программа по математике (геометрия, 9 класс)

Пояснительная записка.

Рабочая программа по школьному курсу «Геометрия» для 9 класса составлена на основе Федерального компонента государственного стандарта основного общего образования.

Данная рабочая программа ориентирована на учащихся 9 класса и реализуется на основе следующих документов:

Стандарт основного общего образования по математике // Сборник нормативно-правовых документов и методических материалов, Москва: «Вентана-Граф», 2008.

Геометрия. Сборник рабочих программ 7 – 9 классы / Сост. Т.А. Бурмистрова – Москва: «Просвещение», 2014.

Рабочая программа соответствует базовому уровню подготовки школьников по Стандарту основного общего образования, конкретизирует содержание тем и даёт распределение часов по разделам курса.

Программа соответствует учебнику «Геометрия 7-9» для образовательных учреждений / Л.С. Атанасян, В.Ф. Бутузов, С.Б.Кадомцев, Э.Г.Позняк, И.И.Юдина. – М.: Просвещение, 2014 г.

Цели курса:

Изучение геометрии на ступени основного общего образования направлено на достижение следующих целей:

овладение системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования;

интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе: ясности и точности мысли, критичности мышления, интуиции, логического мышления, элементов алгоритмической культуры, пространственных представлений, способности к преодолению трудностей;

формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов;

воспитание культуры личности, отношения к математике как к части общечеловеческой культуры, играющей особую роль в общественном развитии.

При изучении геометрии на ступени основного общего образования ставятся следующие задачи:

приобретение знаний и умений для использования в практической деятельности и повседневной жизни;

овладение способами познавательной, информационно-коммуникативной и рефлексивной деятельностью;

освоение познавательной, информационной, коммуникативной, рефлексивной компетенциями;

освоение общекультурной, практической математической, социально-личностной компетенциями, что предполагает:

общекультурную компетентность (формирование представлений об идеях и методах математики, о математике как универсальном языке науки, средстве моделирования явлений и процессов; формирование понимания, что геометрические формы являются идеализированными образами реальных объектов);

практическую математическую компетентность (овладение языком геометрии в устной и письменной форме, геометрическими знаниями и умениями, необходимыми для изучения школьных естественнонаучных дисциплин, овладение практическими навыками использования геометрических инструментов для изображения фигур, нахождения их размеров);

социально-личностную компетентность (развитие логического мышления, алгоритмической культуры, пространственного воображения, овладения навыками дедуктивных рассуждений, интуиции, которые необходимы для получения образования и для самостоятельной деятельности; формирование умения проводить аргументацию своего выбора или хода решения задачи; воспитание средствами математики культуры личности через знакомство с историей геометрии, эволюцией геометрических идей).

Основные развивающие и воспитательные цели:

Развитие:

ясности и точности мысли, критичности мышления, интуиции, логического мышления, элементов алгоритмической культуры, пространственных представлений, способности к преодолению трудностей;

математической речи;

внимания; памяти;

навыков само и взаимопроверки.

Формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов.

Воспитание:

культуры личности, отношения к математике как к части общечеловеческой культуры, понимание значимости математики для научно-технического прогресса;

волевых качеств;

коммуникабельности;

ответственности.

Общая характеристика курса.

Содержание программы направлено на освоение обучающимися базовых знаний и формирование базовых компетентностей, что соответствует требованиям основной образовательной программы основного общего образования МБОУ Новопавловский УВК. Рабочая программа включает все темы, предусмотренные для изучения Федеральным государственным образовательным стандартом основного общего образования по математике и авторской программой Т. А. Бурмистровой Геометрия. Сборник рабочих программ 7 – 9 классы / Сост. Т.А. Бурмистрова – Москва: «Просвещение», 2014.

В курсе геометрии 9 класса условно выделены шесть основных разделов: векторы, метод координат, соотношения между сторонами и углами треугольника и скалярное произведение векторов, длина окружности и площадь круга, движения, начальные сведения из стереометрии.

Раздел 1. Векторы.

Вектор определяется как направленный отрезок и действия над векторами вводятся так, как это принято в физике, т. е. как действия с направленными отрезками. Основное внимание должно быть уделено выработке умений выполнять операции над векторами (складывать векторы по правилам треугольника и параллелограмма, строить вектор, равный разности двух данных векторов, а также вектор, равный произведению данного вектора на данное число).

Цели изучения раздела:

научить учащихся выполнять действия над векторами как направленными отрезками, что важно для применения векторов в физике.

Раздел 2. Метод координат.

На примерах показывается, как векторы могут применяться к решению геометрических задач. Демонстрируется эффективность применения формул для координат середины отрезка, расстояния между двумя точками, уравнений окружности и прямой в конкретных геометрических задачах, тем самым дается представление об изучении геометрических фигур с помощью методов алгебры.

Весь материал - в документе.

Муниципальное бюджетное общеобразовательное учреждение

"Новопавловский учебно-воспитательный комплекс" муниципального образования

Красноперекопский район Республики Крым

РАБОЧАЯ ПРОГРАММА

по геометрии

на 2014/2015 учебный год

Уровень образования - основное общее образование, 9 класс.

Уровень изучения предмета - базовый

Учитель Ганиева Эвелина Акимовна

2015 г.

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА

Рабочая программа по школьному курсу «Геометрия» для 9 класса составлена на основе Федерального компонента государственного стандарта основного общего образования.

Данная рабочая программа ориентирована на учащихся 9 класса и реализуется на основе следующих документов:

1. Стандарт основного общего образования по математике // Сборник нормативно-правовых документов и методических материалов, Москва: «Вентана-Граф», 2008.

2. Геометрия. Сборник рабочих программ 7 – 9 классы / Сост. Т.А. Бурмистрова – Москва: «Просвещение», 2014.

Рабочая программа соответствует базовому уровню подготовки школьников по Стандарту основного общего образования, конкретизирует содержание тем и даёт распределение часов по разделам курса.

Программа соответствует учебнику «Геометрия 7-9» для образовательных учреждений / Л.С. Атанасян, В.Ф. Бутузов, С.Б.Кадомцев, Э.Г.Позняк, И.И.Юдина. – М.: Просвещение, 2014 г.

ЦЕЛИ КУРСА

Изучение геометрии на ступени основного общего образования направлено на достижение следующих целей:

• овладение системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования;

• интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе: ясности и точности мысли, критичности мышления, интуиции, логического мышления, элементов алгоритмической культуры, пространственных представлений, способности к преодолению трудностей;

• формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов;

• воспитание культуры личности, отношения к математике как к части общечеловеческой культуры, играющей особую роль в общественном развитии.

При изучении геометрии на ступени основного общего образования ставятся следующие задачи:

• приобретение знаний и умений для использования в практической деятельности и повседневной жизни;

• овладение способами познавательной, информационно-коммуникативной и рефлексивной деятельностью;

• освоение познавательной, информационной, коммуникативной, рефлексивной компетенциями;

• освоение общекультурной, практической математической, социально-личностной компетенциями, что предполагает:

• общекультурную компетентность (формирование представлений об идеях и методах математики, о математике как универсальном языке науки, средстве моделирования явлений и процессов; формирование понимания, что геометрические формы являются идеализированными образами реальных объектов);

• практическую математическую компетентность (овладение языком геометрии в устной и письменной форме, геометрическими знаниями и умениями, необходимыми для изучения школьных естественнонаучных дисциплин, овладение практическими навыками использования геометрических инструментов для изображения фигур, нахождения их размеров);

• социально-личностную компетентность (развитие логического мышления, алгоритмической культуры, пространственного воображения, овладения навыками дедуктивных рассуждений, интуиции, которые необходимы для получения образования и для самостоятельной деятельности; формирование умения проводить аргументацию своего выбора или хода решения задачи; воспитание средствами математики культуры личности через знакомство с историей геометрии, эволюцией геометрических идей).

Основные развивающие и воспитательные цели:

Развитие:

• ясности и точности мысли, критичности мышления, интуиции, логического мышления, элементов алгоритмической культуры, пространственных представлений, способности к преодолению трудностей;

• математической речи;

• внимания; памяти;

• навыков само и взаимопроверки.

Формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов.

Воспитание:

• культуры личности, отношения к математике как к части общечеловеческой культуры, понимание значимости математики для научно-технического прогресса;

• волевых качеств;

• коммуникабельности;

• ответственности.

ОБЩАЯ ХАРАКТЕРИСТИКА КУРСА

Содержание программы направлено на освоение обучающимися базовых знаний и формирование базовых компетентностей, что соответствует требованиям основной образовательной программы основного общего образования МБОУ Новопавловский УВК. Рабочая программа включает все темы, предусмотренные для изучения Федеральным государственным образовательным стандартом основного общего образования по математике и авторской программой Т. А. Бурмистровой Геометрия. Сборник рабочих программ 7 – 9 классы / Сост. Т.А. Бурмистрова – Москва: «Просвещение», 2014.

В курсе геометрии 9 класса условно выделены шесть основных разделов: векторы, метод координат, соотношения между сторонами и углами треугольника и скалярное произведение векторов, длина окружности и площадь круга, движения, начальные сведения из стереометрии.

Раздел 1. Векторы

Вектор определяется как направленный отрезок и действия над векторами вводятся так, как это принято в физике, т. е. как действия с направленными отрезками. Основное внимание должно быть уделено выработке умений выполнять операции над векторами (складывать векторы по правилам треугольника и параллелограмма, строить вектор, равный разности двух данных векторов, а также вектор, равный произведению данного вектора на данное число).

Цели изучения раздела:

• научить учащихся выполнять действия над векторами как направленными отрезками, что важно для применения векторов в физике.

Раздел 2. Метод координат

На примерах показывается, как векторы могут применяться к решению геометрических задач. Демонстрируется эффективность применения формул для координат середины отрезка, расстояния между двумя точками, уравнений окружности и прямой в конкретных геометрических задачах, тем самым дается представление об изучении геометрических фигур с помощью методов алгебры.

Цели изучения раздела:

• познакомить обучающихся с использованием векторов и метода координат при решении геометрических задач.

Раздел 3. Соотношения между сторонами и углами треугольника. Скалярное произведение векторов

Синус и косинус любого угла от 0° до 180° вводятся с помощью единичной полуокружности, доказываются теоремы синусов и косинусов и выводится еще одна формула площади треугольника (половина произведения двух сторон на синус угла между ними). Этот аппарат применяется к решению треугольников. Скалярное произведение векторов вводится как в физике (произведение длин векторов на косинус угла между ними). Рассматриваются свойства скалярного произведения и его применение при решении геометрических задач. Основное внимание следует уделить выработке прочных навыков в применении тригонометрического аппарата при решении геометрических задач.

Цели изучения раздела:

• развить умение учащихся применять тригонометрический аппарат при решении геометрических задач.

Раздел 4. Длина окружности и площадь круга

В начале темы дается определение правильного многоугольника и рассматриваются теоремы об окружностях, описанной около правильного многоугольника и вписанной в него. С помощью описанной окружности решаются задачи о построении правильного шестиугольника и правильного 2n-угольника, если дан правильный n-угольник. Формулы, выражающие сторону правильного многоугольника и радиус вписанной в него окружности через радиус описанной окружности, используются при выводе формул длины окружности и площади круга. Вывод опирается на интуитивное представление о пределе: при неограниченном увеличении числа сторон правильного многоугольника, вписанного в окружность, его периметр стремится к длине этой окружности, а площадь - к площади круга, ограниченного окружностью.

Цели изучения раздела:

• расширить знание учащихся о многоугольниках;

• рассмотреть понятия длины окружности и площади круга и формулы для их вычисления.

Раздел 5. Движения

Движение плоскости вводится как отображение плоскости на: себя, сохраняющее расстояние между точками. При рассмотрении видов движений основное внимание уделяется построению образов точек, прямых, отрезков, треугольников при осевой и центральной симметриях, параллельном переносе, повороте. На эффектных примерах показывается применение движений при решении геометрических задач. Понятие наложения относится в данном курсе к числу основных понятий. Доказывается, что понятия наложения и движения являются эквивалентными: любое наложение является движением плоскости и обратно. Изучение доказательства не является обязательным, однако следует рассмотреть связь понятий наложения и движения.

Цели изучения раздела:

• познакомить учащихся с понятием движения и его свойствами, с основными видами движений, со взаимоотношениями наложений и движений.

Раздел 6. Начальные сведения из стереометрии

Рассмотрение простейших многогранников (призмы, параллелепипеда, пирамиды), а также тел и поверхностей вращения (цилиндра, конуса, сферы, шара) проводится на основе наглядных представлений, без привлечения аксиом стереометрии. Формулы для вычисления объемов указанных тел выводятся на основе принципа Кавальери, формулы для вычисления площадей боковых поверхностей цилиндра и конуса получаются с помощью разверток этих поверхностей, формула площади сферы приводится без обоснования.

Цели изучения раздела:

• дать начальное представление о телах и поверхностях в пространстве;

• познакомить учащихся с основными формулами для вычисления площадей поверхностей и объемов тел.

ОПИСАНИЕ МЕСТА КУРСА В УЧЕБНОМ ПЛАНЕ

На преподавание геометрии в 9 классе отведено 2 часа в неделю, всего 70 часов в год, из них 1 час – на диагностическую контрольную работу, 4 часа - на тематические контрольные работы и 1 час - на итоговую контрольную работу.

ПЛАНИРУЕМЫЕ РЕЗУЛЬТАТЫ ОСВОЕНИЯ КУРСА ОБУЧАЮЩИМИСЯ

Изучение математики в основной школе дает воз­можность обучающимся достичь следующих результа­тов развития:

1. В направлении личностного развития:

• формирование ответственного отношения к учению, готовность и способности обучающихся к саморазвитию и самообразованию на основе мотивации к обучению и познанию, выбору дальнейшего образования на базе ориентировки в мире профессий и профессиональных предпочтений, осознанному построению индивидуальной образовательной траектории с учётом устойчивых познавательных интересов;

• формирование целостного мировоззрения, соответствующего современному уровню развития науки и общественной практики;

• формирование коммуникативной компетентности в общении и сотрудничестве со сверстниками, старшими и младшими в образовательной, общественно полезной, учебно-исследовательской, творческой и других видах деятельности;

• умение ясно, точно, грамотно излагать свои мысли в устной и письменной речи, понимать смысл поставленной задачи, выстраивать аргументацию, приводить примеры и контрпримеры;

• критичность мышления, умение распознавать логически некорректные высказывания, отличать гипотезу от факта;

• креативность мышления, инициативу, находчивость, активность при решении геометрических задач;

• умение контролировать процесс и результат учебной математической деятельности;

• способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений.

1. В метапредметном направлении:

• умение самостоятельно планировать альтернативные пути достижения целей, осознанно выбирать наиболее эффективные способы решения учебных и познавательных задач;

• умение осуществлять контроль по результату и по способу действия на уровне произвольного внимания и вносить необходимые коррективы;

• умение адекватно оценивать правильность или ошибочность выполнения учебной задачи, ее объективную трудность и собственные возможности ее решения;

• осознанное владение логическими действиями определения понятий, обобщения, установления аналогий, классификации на основе самостоятельного выбора оснований и критериев, установления родовидовых связей;

• умение устанавливать причинно-следственные связи, строить логическое рассуждение, умозаключение (индуктивное, дедуктивное и по аналогии) и выводы;

• умение создавать, применять и преобразовывать знако-символические средства, модели и схемы для решения учебных и познавательных задач;

• умение организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками: определять цели, распределять функции и роли участников, общие способы работы; умение работать в группе: находить общее решение и разрешать конфликты на основе согласования позиций и учета интересов; слушать партнера; формулировать, аргументировать и отстраивать свое мнение;

• формирование и развитие учебной и общепользовательской компетентности в области использования информационно-коммуникационных технологий (ИКТ–компетентности);

• первоначальные представления об идеях и о методах математики как об универсальном языке науки и техники, о средстве моделирования процессов и явлений;

• умение видеть математическую задачу в контексте проблемной ситуации в других дисциплинах, в окружающей жизни;

• умение находить в различных источниках информацию, необходимую для решения математических проблем, и представлять ее в понятной форме; принимать решение в условиях неполной и избыточной, точной и вероятностной информации;

• умение понимать и использовать математические средства наглядности (рисунки, чертежи, схемы и др.) для иллюстрации, интерпретации, аргументации;

• умение выдвигать гипотезы при решении учебных задач и понимать необходимость их проверки;

• умение применять индуктивные и дедуктивные способы рассуждений, видеть различные стратегии решения задач;

• понимание сущности алгоритмических предписаний и умение действовать в соответствии с предложенным алгоритмом;

• умение самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем;

• умение планировать и осуществлять деятельность, направленную на решение задач исследовательского характера.

1. В предметном направлении:

• овладение базовым понятийным аппаратом по основным разделам содержания; представление об основных изучаемых понятиях (число, геометрическая фигура) как важнейших математических моделях, позволяющих описывать и изучать реальные процессы и явления;

• умение работать с геометрическим текстом (анализировать, извлекать необходимую информацию), точно и грамотно выражать свои мысли в устной и письменной речи с использованием математической терминологии и символики, использовать различные языки математики, проводить классификации, логические обоснования, доказательства математических утверждений;

• овладение навыками устных, письменных, инструментальных вычислений;

• овладение геометрическим языком, умение использовать его для описания предметов окружающего мира, развитие пространственных представлений и изобразительных умений, приобретение навыков геометрических построений;

• усвоение систематических знаний о плоских фигурах и их свойствах, а также на наглядном уровне – о простейших пространственных телах, умение применять систематические знания о них для решения геометрических и практических задач;

• умение измерять длины отрезков, величины углов, использовать формулы для нахождения периметров, площадей геометрических фигур;

• умение применять изученные понятия, результаты, методы для решения задач практического характера и задач из смежных дисциплин с использованием при необходимости справочных материалов, калькулятора, компьютера.

СОДЕРЖАНИЕ КУРСА

тематический план

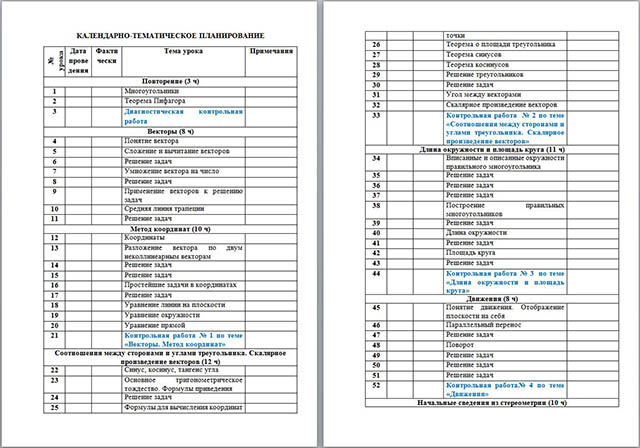
КАЛЕНДАРНО-ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ

КРИТЕРИИ ОЦЕНИВАНИЯ ОБУЧАЮЩИХСЯ

1. Оценка письменных контрольных работ обучающихся по математике.

Отметка «5» ставится, если:

• работа выполнена полностью;

• в логических рассуждениях и обосновании решения нет пробелов и ошибок;

• в решении нет математических ошибок (возможна одна неточность, описка, которая не является следствием незнания или непонимания учебного материала).

Отметка «4» ставится, если:

• работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки);

• допущены одна ошибка или есть два – три недочёта в выкладках, рисунках, чертежах или графиках (если эти виды работ не являлись специальным объектом проверки).

Отметка «3» ставится, если:

• допущено более одной ошибки или более двух – трех недочетов в выкладках, чертежах или графиках, но обучающийся обладает обязательными умениями по проверяемой теме.

Отметка «2» ставится, если:

• допущены существенные ошибки, показавшие, что обучающийся не обладает обязательными умениями по данной теме в полной мере.

Учитель может повысить отметку за оригинальный ответ на вопрос или оригинальное решение задачи, которые свидетельствуют о высоком математическом развитии обучающегося; за решение более сложной задачи или ответ на более сложный вопрос, предложенные обучающемуся дополнительно после выполнения им каких-либо других заданий.

2. Оценка устных ответов обучающихся по математике.

Ответ оценивается отметкой «5», если ученик:

• полно раскрыл содержание материала в объеме, предусмотренном программой и учебником;

• изложил материал грамотным языком, точно используя математическую терминологию и символику, в определенной логической последовательности;

• правильно выполнил рисунки, чертежи, графики, сопутствующие ответу;

• показал умение иллюстрировать теорию конкретными примерами, применять ее в новой ситуации при выполнении практического задания;

• продемонстрировал знание теории ранее изученных сопутствующих тем, сформированность и устойчивость используемых при ответе умений и навыков;

• отвечал самостоятельно, без наводящих вопросов учителя;

• возможны одна – две неточности при освещении второстепенных вопросов или в выкладках, которые ученик легко исправил после замечания учителя.

Ответ оценивается отметкой «4», если удовлетворяет в основном требованиям на оценку «5», но при этом имеет один из недостатков:

• в изложении допущены небольшие пробелы, не исказившее математическое содержание ответа;

• допущены один – два недочета при освещении основного содержания ответа, исправленные после замечания учителя;

• допущены ошибка или более двух недочетов при освещении второстепенных вопросов или в выкладках, легко исправленные после замечания учителя.

Отметка «3» ставится в следующих случаях:

• неполно раскрыто содержание материала (содержание изложено фрагментарно, не всегда последовательно), но показано общее понимание вопроса и продемонстрированы умения, достаточные для усвоения программного материала;

• имелись затруднения или допущены ошибки в определении математической терминологии, чертежах, выкладках, исправленные после нескольких наводящих вопросов учителя;

• ученик не справился с применением теории в новой ситуации при выполнении практического задания, но выполнил задания обязательного уровня сложности по данной теме;

• при достаточном знании теоретического материала выявлена недостаточная сформированность основных умений и навыков.

Отметка «2» ставится в следующих случаях:

• не раскрыто основное содержание учебного материала;

• обнаружено незнание учеником большей или наиболее важной части учебного материала;

• допущены ошибки в определении понятий, при использовании математической терминологии, в рисунках, чертежах или графиках, в выкладках, которые не исправлены после нескольких наводящих вопросов учителя.

Контроль уровня обученности

Контроль за результатами обучения осуществляется через использование следующих видов контроля: входной, текущий, тематический и итоговый. При этом используются различные формы контроля: контрольная работа, домашняя контрольная работа, самостоятельная работа, домашняя практическая работа, домашняя самостоятельная работа, тест, контрольный тест, устный опрос, блиц-опрос, фронтальный опрос.

Принятые обозначения:

КР – контрольная работа;

СР – самостоятельная работа;

ПР – проверочная работа;

КТ – контрольный тест;

Т – тестовая работа;

ФО – фронтальный опрос;

УО – устный опрос;

БО - блиц опрос;

ДКР – домашняя контрольная работа.

УЧЕБНО-МЕТОДИЧЕСКОЕ И МАТЕРИАЛЬНО-ТЕХНИЧЕСКОЕ ОБЕСПЕЧЕНИЕ ОБРАЗОВАТЕЛЬНОГО ПРОЦЕССА

Учебно-методический комплекс:

1. Геометрия. Учебник для 7-9 классов общеобразовательных организаций. Л.С. Атанасян, В.Ф.Бутузов, и др.. – М: «Просвещение», 2014.

2. Программа общеобразовательных учреждений: Сборник «Программы для общеобразовательных учреждений». Геометрия. 7-9 кл./ Сост. Т.А. Бурмистрова. М.: «Просвещение», 2011.

3. Стандарт основного общего образования по математике.

4. Научно-теоретический и методический журнал «Математика в школе».

5. Еженедельное учебно-методическое приложение к газете «Первое сентября» Математика.

Для обеспечения плодотворного учебного процесса предполагается использование информа­ции и материалов следующих интернет-ресурсов:

1. Единая коллекция цифровых образовательных ресурсов [Электронный ресурс]. / Режим доступа: http://school-collection.edu.ru

2. Учительский портал [Электронный ресурс]. / Режим доступа: www.uchportal.ru

3. Фестиваль педагогических идей «Открытый урок» [Электронный ресурс]. / Режим доступа: http://festival.1september.ru/articles/411439

4. Сообщество взаимопомощи учителей [Электронный ресурс]. / Режим доступа: http://pedsovet.su/load/136

5. Видеоуроки в Интернет [Электронный ресурс]. / Режим доступа: http://videouroki.net/filecom.php?fileid=98657940

6. Социальная сеть работников образования [Электронный ресурс]. / Режим доступа: http://nsportal.ru

7. Библиотека методических материалов для учителя [Электронный ресурс]. / Режим доступа: http://infourok.ru