МБОУ «Средняя общеобразовательная школа с углубленным изучением отдельных предметов №3»
Рабочая учебная программа
по геометрии
для учащихся 10 класса «А» (углубленный).
Год разработки: 2012
Срок реализации программы 2012-2013 учебный год.
Составлена на основе Примерной программы основного общего образования с учетом требований федерального компонента государственного стандарта общего образования и с учетом программ для общеобразовательных школ, гимназий, лицеев (Кузнецова Г.М., Миндюк Н.Г. Математика 5-11 кл. – М.: Дрофа, 2004)
Программу составила Конкина Надежда Васильевна
г. Ханты-Мансийск
2012-2013 учебный год
РАБОЧАЯ ПРОГРАММА
курса «Геометрии»
10 класс (по учебнику : Л.С.Атанасян «Геометрия 10-11кл»)
Пояснительная записка
Рабочая программа по геометрии для 10 класса составлена на основе примерной программы среднего общего образования и авторской программы Л. С. Атанасяна, В.Ф. Бутузова, С.Б. Кадомцева и др. / Программы общеобразовательных учреждений. Геометрия. 10-11 классы. Москва. Просвещение.2009/, в соответствии с требованиями федерального компонента государственного образовательного стандарта среднего общего образования.
Рабочая программа конкретизирует содержание предметных тем образовательного стандарта и дает распределение учебных часов по разделам курса.
Рабочая программа выполняет две основные функции:
Информационно-методическая функция позволяет всем участникам образовательного процесса получить представление о целях, содержании, общей стратегии обучения, воспитания и развития учащихся средствами данного учебного предмета.
Организационно-планирующая функция предусматривает выделение этапов обучения, структурирование учебного материала, определение его количественных и качественных характеристик на каждом из этапов, в том числе для содержательного наполнения промежуточной аттестации учащихся.
Реализация рабочей программы осуществляется с использованием учебно-методического комплекта:
-Л. С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцева и др. Геометрия. Учебник для 10-11 классов общеобразовательных учреждений. Базовый и профильный уровень. Москва. Просвещение.2007
-Б.Г. Зив. Дидактические материалы по геометрии для 10 класса. Москва. Просвещение.2007
-С.М. Саакян, В.Ф. Бутузов. Изучение геометрии в 10-11 классах. Книга для учителя. Москва. Просвещение.2007
Дополнительная литература:
В.А. Яровенко Поурочные разработки по геометрии. Дифференцированный подход, 10 класс. Москва. «ВАКО». 2006
Е.М. Рабинович Математика. Задачи на готовых чертежах. Геометрия. 10-11 классы. Москва. ИЛЕКСА. 2008
А.П. Ершова, В.В. Голобородько. Математика. Устные проверочные и зачётные работы. Устная геометрия. 10-11 классы. Москва. ИЛЕКСА. 2005
Изучение геометрии в 10 классе на базовом уровне направлено на достижение следующих целей:
развитие логического мышления, пространственного воображения и интуиции, критичности мышления на уровне, необходимом для продолжения образования и самостоятельной деятельности в области математики и её производных, в будущей профессиональной деятельности;
воспитание средствами геометрии культуры личности: отношения к математике как части общечеловеческой культуры.
развитие логического мышления, пространственного воображения, алгоритмической культуры, критичности мышления на уровне, необходимом для обучения в высшей школе по соответствующей специальности, в будущей профессиональной деятельности;
овладение математическими знаниями и умениями, необходимыми в повседневной жизни, для изучения школьных естественнонаучных дисциплин на базовом уровне, для получения образования в областях, не требующих углубленной математической подготовки
Текущий контроль осуществляется в виде самостоятельных работ, зачётов, письменных тестов, математических диктантов, устных и письменных опросов по теме урока, контрольных работ по разделам учебника. Всего 13 контрольных работ.
Обязательный минимум содержания
основных образовательных программ
Геометрия
Прямые и плоскости в пространстве. Основные понятия стереометрии (точка, прямая, плоскость, пространство).
Пересекающиеся, параллельные и скрещивающиеся прямые. Угол между прямыми в пространстве. Перпендикулярность прямых. Параллельность и перпендикулярность прямой и плоскости, признаки и свойства. Теорема о трех перпендикулярах. Перпендикуляр и наклонная. Угол между прямой и плоскостью.
Параллельность плоскостей, перпендикулярность плоскостей, признаки и свойства. Двугранный угол, линейный угол двугранного угла.
Расстояния от точки до плоскости. Расстояние от прямой до плоскости. Расстояние между параллельными плоскостями. Расстояние между скрещивающимися прямыми.
Параллельное проектирование. Площадь ортогональной проекции многоугольника. Изображение пространственных фигур.
Многогранники. Вершины, ребра, грани многогранника. Развертка. Многогранные углы. Выпуклые многогранники. Теорема Эйлера.
Призма, ее основания, боковые ребра, высота, боковая поверхность. Прямая и наклонная призма. Правильная призма. Параллелепипед. Куб.
Пирамида, ее основание, боковые ребра, высота, боковая поверхность. Треугольная пирамида. Правильная пирамида. Усеченная пирамида.
Симметрии в кубе, в параллелепипеде, в призме и пирамиде. Понятие о симметрии в пространстве (центральная, осевая, зеркальная). Примеры симметрий в окружающем мире.
Сечения куба, призмы, пирамиды.
Представление о правильных многогранниках (тетраэдр, куб, октаэдр, додекаэдр и икосаэдр).
Тела и поверхности вращения. Цилиндр и конус. Усеченный конус. Основание, высота, боковая поверхность, образующая, развертка. Осевые сечения и сечения параллельные основанию.
Шар и сфера, их сечения, касательная плоскость к сфере.
Объемы тел и площади их поверхностей. Понятие об объеме тела. Отношение объемов подобных тел.
Формулы объема куба, прямоугольного параллелепипеда, призмы, цилиндра. Формулы объема пирамиды и конуса. Формулы площади поверхностей цилиндра и конуса. Формулы объема шара и площади сферы.
Координаты и векторы. Декартовы координаты в пространстве. Формула расстояния между двумя точками. Уравнения сферы и плоскости. Формула расстояния от точки до плоскости.
Векторы. Модуль вектора. Равенство векторов. Сложение векторов и умножение вектора на число. Угол между векторами. Координаты вектора. Скалярное произведение векторов.
Требования к уровню подготовки выпускников
В результате изучения геометрии на базовом уровне ученик должен
знать/понимать
значение математической науки для решения задач, возникающих в теории и практике; широту и в то же время ограниченность применения математических методов к анализу и исследованию процессов и явлений в природе и обществе;
значение практики и вопросов, возникающих в самой математике для формирования и развития математической науки; историю возникновения и развития геометрии;
универсальный характер законов логики математических рассуждений, их применимость во всех областях человеческой деятельности;
вероятностный характер различных процессов окружающего мира.
Уметь:
распознавать на чертежах и моделях пространственные формы; соотносить трехмерные объекты с их описаниями, изображениями;
описывать взаимное расположение прямых и плоскостей в пространстве, аргументировать свои суждения об этом расположении;
анализировать в простейших случаях взаимное расположение объектов в пространстве;
изображать основные многогранники и круглые тела; выполнять чертежи по условиям задач;
строить простейшие сечения куба, призмы, пирамиды;
решать планиметрические и простейшие стереометрические задачи на нахождение геометрических величин (длин, углов, площадей, объемов);
использовать при решении стереометрических задач планиметрические факты и методы;
проводить доказательные рассуждения в ходе решения задач.
Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
исследования (моделирования) несложных практических ситуаций на основе изученных формул и свойств фигур;
вычисления объемов и площадей поверхностей пространственных тел при решении практических задач, используя при необходимости справочники и вычислительные устройства.
Учебно-тематический план
| № п/п | Тема | Количество часов | В том числе |
| Контрольные работы |
| 1. | Введение. Аксиомы стереометрии | 5 | 1 |
| 2. | Параллельность прямых и плоскостей | 25 | 4 |
| 3 | Перпендикулярность прямых и плоскостей | 26 | 3 |
| 4 | Многогранники | 22 | 2 |
| 5 | Векторы и координаты в пространстве | 16 | 2 |
| 6 | Повторение | 9 | 1 |
|
| Итого | 105 | 13 |
Содержание тем учебного курса.
1. Введение . Аксиомы стереометрии и их следствия.(5 часов,)
Предмет стереометрии . Аксиомы стереометрии. Некоторые свойства из аксиом. Решение задач на применение аксиом стереометрии и их следствий.
Основная цель:
Сформировать представления учащихся об основных понятиях и аксиомах стереометрии , их использовании при решении задач.
Методы:
Решение стандартных задач логического характера, а так же изображение точек, прямых и плоскостей на проекционном чертеже при различном их взаимном расположении в пространстве.
Знать:
Аксиомы о взаимном расположении точек, прямых и плоскостей в пространстве и их следствия.
Уметь:
Применять аксиомы стереометрии и их следствия при решении задач.
2. Параллельность прямых и плоскостей (25 часов, из них 6 часов - контрольные работы)
Основная цель :
Дать учащимся систематические сведения о параллельности прямых и плоскостей в пространстве. Осуществить знакомство с простейшими многогранниками. Познакомить с различными способами изображения пространственных фигур на плоскости. Сформировать умения решать задачи на доказательства (метод от противного).Строить сечения тетраэдра и параллелепипеда.
Методы:
Используется метод доказательств от противного, знакомого учащимся из курса планиметрии. Решение большого количества логических задач.
2.1.Взаимное расположение прямых в пространстве. Угол между двумя прямыми(6)
Скрещивающиеся прямые. Углы с сонаправленными сторонами. Угол между прямыми. Решение задач по теме «Взаимное расположение прямых в пространстве. Угол между двумя прямыми. Решение задач по теме «Параллельность прямых и плоскостей
Знать:
Понятие скрещивающиеся прямых. Теорему о равенстве углов с сонаправленными сторонами.
Уметь:
Находить угол между прямыми в пространстве. Применять полученные знания при решении задач.
2.2. Взаимное расположение прямой и плоскости(9 часов)
Параллельные прямые в пространстве. Параллельность прямой и плоскости. Решение задач по теме «Параллельность прямой и плоскости»
Знать:
Виды расположения прямых в пространстве. Понятия параллельных и скрещивающихся прямых. Теоремы о параллельности прямых и параллельности 3-х прямых. Расположение в пространстве прямой и плоскости. Понятие параллельности прямой и плоскости (признак параллельности прямой и плоскости).
Уметь:
Рассматривать понятие взаимного расположения прямых , прямой и плоскости на моделях куба, призмы, пирамиды. Применять изученные теоремы к решению задач. Самостоятельно выбрать способ решения задач.
2.3. Параллельность плоскостей (6 часов)
Параллельные плоскости. Признак параллельности плоскостей. Свойства параллельных плоскостей.
Знать:
Понятие параллельных плоскостей. Признак параллельности двух плоскостей. Свойства параллельных плоскостей.
Уметь:
Доказывать признак параллельности двух плоскостей и применять его при решении задач. Использовать свойства параллельных плоскостей при решении задач.
2.4.Тетраэдр. Параллелепипед(6)
Тетраэдр. Параллелепипед. Задачи на построение сечений. Корректировка знаний учащихся .Контрольная работа.
Знать:
Понятие тетраэдра. Понятие параллелепипеда и его свойства. Способы построения сечений тетраэдра и параллелепипеда.
Уметь:
Работать с чертежом и читать его. Решать задачи , связанные с тетраэдром Решать задачи на применение свойств параллелепипеда. Строить сечение тетраэдра и параллелепипеда.
3.Перпендикулярность прямых и плоскостей(26 часов, из них 5 часов - контрольные работы)
Основная цель:
Дать учащимся систематические сведения о перпендикулярности прямых и плоскостей в пространстве .Ввести понятие углов между прямыми и плоскостями, между плоскостями.
Методы:
Обобщаются и систематизируются знания учащихся о перпендикулярных прямых, перпендикуляре и наклонных, известные из курса планиметрии, что будет способствовать более глубокому усвоению темы. Постоянное обращение к теоремам, свойствам и признакам курса планиметрии при решении задач по изучаемой теме.
3.1.Перпендикулярность прямой и плоскости(5)
Перпендикулярные прямые в пространстве. Параллельные прямые, перпендикулярные
к плоскости. Признак перпендикулярности прямой и плоскости. Теорема о прямой, перпендикулярной плоскости. Решение задач на перпендикулярность прямо и плоскости.
Знать:
Понятие перпендикулярных прямых. Лемму перпендикулярности двух параллельных прямых к третей. Определение перпендикулярности прямой и плоскости. Связь между параллельностью прямых и их перпендикулярностью к плоскости. Признак перпендикулярности прямой и плоскости.
Уметь :
Доказывать Лемму перпендикулярности двух параллельных прямых к третьей. Применять признак перпендикулярности прямой и плоскости к решению задач. Находить связь между параллельностью прямых и их перпендикулярностью к плоскости. Решать основные типы задач на перпендикулярность прямой и плоскости.
3.2. Перпендикуляр и наклонная. Угол между прямой и плоскостью(7).
Расстояние от точки до плоскости. Теорема о трех перпендикулярах. Угол между прямой и плоскостью. Повторение теории. Решение задач на применение теоремы о трех перпендикулярах. Угол между прямой и плоскостью.
Знать: Понятие расстояние от точки до прямой. Теорему о трех перпендикулярах. Понятие угла между прямой и плоскостью.
Уметь: Доказывать теорему о трех перпендикулярах и использовать ее при решении задач. Находить угол между прямой и плоскостью.
3.3. Двугранный угол. Перпендикулярность плоскостей (14)
Двугранный угол. Признак перпендикулярности двух плоскостей. Прямоугольный параллелепипед. Решение задач на свойства прямоугольного параллелепипеда. Повторение теории и решении задач по теме «Перпендикулярность прямых и плоскостей», Решение.
Знать: Понятие двугранного угла и его линейного угла. Понятие угла между плоскостями. Определение перпендикулярных плоскостей. Признак перпендикулярности двух плоскостей. Понятие прямоугольного параллелепипеда, свойства его граней, диагоналей двугранных углов.
Уметь: Определять угол между плоскостями. Применять признак перпендикулярности двух плоскостей при решении задач, работать с чертежом и читать его. Использовать свойства прямоугольного параллелепипеда при решении задач.
4. Многогранники (22 часа, из них 3 часа - контрольные работы)
Основная цель: дать учащимся систематические сведения об основных видах многогранников.
Методы: изучение многогранников нужно вести на наглядной основе, опираясь на объекты природы, предметы окружающей действительности.
4.1. Понятие многогранника. (9 часов)
Трехгранные углы. Теорема о сумме плоских углов трехгранного и многогранного углов. Понятие многогранника и его элементов.
Знать: Понятие трехгранного угла. Понятие многогранника. Элементы симметрии правильных многогранников.
Уметь: Работать с чертежом и читать его. Давать описание многогранников.
4.2. Пирамида. Призма (4)
Пирамида. Правильная пирамида. Решение задач по теме пирамида. Усеченная пирамида. Площадь поверхности усеченной пирамиды. Призма. Площадь поверхности призмы. Повторение теории, решение задач на вычисление площади поверхности призмы.
Знать: Понятие пирамиды. Понятие правильной пирамиды. Теорему о площади боковой поверхности правильной пирамиды. Понятие призмы. Виды призм. Понятие площади поверхности призмы. Формулу для вычисления площади поверхности призмы.
Уметь: Работать с чертежом и читать его. Отличать виды пирамид и призм. Доказывать теорему о площади боковой поверхности правильной пирамиды. Решать задачи на нахождение площади боковой поверхности правильной пирамиды. Выводить формулу, для вычисления площади поверхности призмы.
4.3 Правильные многогранники (9)
Симметрия в пространстве . Понятие правильного многогранника . Элементы симметрии правильных многогранников. Корректировка знаний учащихся. Решение задач. Зачет №3.
Знать: Симметрия в пространстве. Пять видов правильных многогранников.
Уметь: Увидеть симметрию в пространстве . Различать виды правильных многогранников. Работать с чертежом и читать его.
5. Векторы в пространстве (16 часов, из них 3 часа - контрольные работы)
Основная цель: Обобщить изученный материал в базовой школе материал о векторах на плоскости, дать систематические сведения о действиях с векторами в пространстве.
Методы: Основное внимание уделяется решению задач , так как при этом учащиеся обладают векторным методом.
5.1. Понятие вектора в пространстве(16)
Понятие вектора. Равенство векторов. Сложение и вычитание векторов. Сумма нескольких векторов. Умножение вектора на число. Определение компланарных векторов. Признаки компланарности трех векторов и правило параллелепипеда, сложения трех некомпланарных векторов. Теорему о разложении вектора по трем некомпланарным векторам.
Знать: Определение вектора. Понятие равных векторов. Обозначения. Правило треугольника и параллелограмма сложения векторов в пространстве. Законы сложения векторов. Два способа разности двух векторов. Правило сложения нескольких векторов в пространстве . Правило умножения векторов на число и его свойства.
Уметь: Работать с чертежом и читать его. Обозначать и читать обозначения. Определять равные вектора. Пользоваться правилом треугольника и параллелограмма при нахождении суммы двух векторов. Находить сумму нескольких векторов. Находить разность векторов двумя способами. Находить векторные суммы не прибегая к рисункам. Умножать векторна число. Выполнять действия над векторами. Разложить вектор по трем некомпланарным векторам. Использовать правило параллелепипеда при сложении трех некомпланарных векторов.
5.2 Координаты в пространстве: Координаты вектора. Связь между координатами вектора и координатами точек. Простейшие задачи в координатах. Скалярное произведение векторов.
Знать: Понятие прямоугольной системы координат в пространстве. Понятие координат вектора в прямоугольной системе координат. Понятие радиус-вектора произвольной точки пространства. Формулы координат середины отрезка, длины вектора через его координаты, расстояние между двумя точками. Понятие угла между векторами. Понятие скалярного произведения векторов. Формулу скалярного произведения в координатах. Свойства скалярного произведения.
Уметь: Строить точки в прямоугольной системе координат по заданным её координатам и находить координаты точки в заданной системе координат. Выполнять действия над векторами с заданными координатами. Доказывать, что координаты точки равны соответствующим координатам её радиус-вектора, координаты любого вектора равны разностям соответствующих координат его конца и начала. Решать простейшие задачи в координатах. Вычислять скалярное произведение векторов и находить угол между векторами по их координатам. Вычислять углы между прямыми и плоскостям.
6. Итоговое повторение курса геометрии (9 часов, из них 2 часа – контрольная работа)
Аксиомы стереометрии . Параллельность прямых и плоскостей . Теорема о трех перпендикулярах, угол между прямой и плоскостью. Векторы в пространстве и их применение к решению задач. Итоговая контрольная работа. Заключительный урок-беседа по курсу 10 кл.
Знать: Теоретический материал курса 10класса. Основные теоретические факты. Наиболее распространенные приемы решения задач.
Уметь: Практически применять теоретический материал . Совершенствовать умения и навыки решения задач.
Тематическое планирование (3 часа в неделю, 105 часов)
| № урока | Тема Дата проведения |
| Введение (5 ч) |
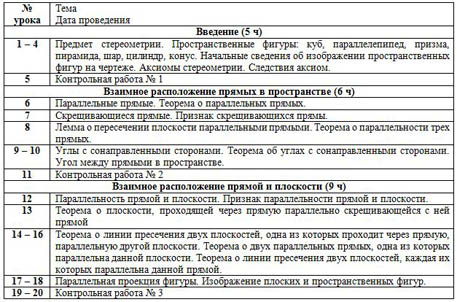
| 1 – 4 | Предмет стереометрии. Пространственные фигуры: куб, параллелепипед, призма, пирамида, шар, цилиндр, конус. Начальные сведения об изображении пространственных фигур на чертеже. Аксиомы стереометрии. Следствия аксиом. |
| 5 | Контрольная работа № 1 |
| Взаимное расположение прямых в пространстве (6 ч) |
| 6 | Параллельные прямые. Теорема о параллельных прямых. |
| 7 | Скрещивающиеся прямые. Признак скрещивающихся прямы. |
| 8 | Лемма о пересечении плоскости параллельными прямыми. Теорема о параллельности трех прямых. |
| 9 – 10 | Углы с сонаправленными сторонами. Теорема об углах с сонаправленными сторонами. Угол между прямыми в пространстве. |
| 11 | Контрольная работа № 2 |
| Взаимное расположение прямой и плоскости (9 ч) |
| 12 | Параллельность прямой и плоскости. Признак параллельности прямой и плоскости. |
| 13 | Теорема о плоскости, проходящей через прямую параллельно скрещивающейся с ней прямой |
| 14 – 16 | Теорема о линии пресечения двух плоскостей, одна из которых проходит через прямую, параллельную другой плоскости. Теорема о двух параллельных прямых, одна из которых параллельна данной плоскости. Теорема о линии пресечения двух плоскостей, каждая их которых параллельна данной прямой. |
| 17 – 18 | Параллельная проекция фигуры. Изображение плоских и пространственных фигур. |
| 19 – 20 | Контрольная работа № 3 |
| Параллельность плоскостей (12 ч) |
| 21 – 22 | Параллельная плоскости. Признак параллельности двух плоскостей. Свойства параллельных плоскостей. |
| 23 | Теорема о существовании и единственности плоскости, проходящей через точку, параллельно данной плоскости. |
| 24 | Теорема о существовании и единственности плоскости, проходящей через точку, не лежащую в данной плоскости, параллельно данной плоскости. |
| 25 | Теорема о параллельности трех плоскостей. |
| 26 | Контрольная работа № 4 |
| 27 – 30 | Параллелепипед и его свойства. Призма. Построение сечений в пирамиде, кубе, призме, параллелепипеде |
| 31 – 32 | Контрольная работа № 5 |
| Перпендикулярность прямой и плоскости (12 ч) |
| 33 – 34 | Прямая, перпендикулярная к плоскости. Лемма о перпендикулярности двух параллельных прямых к третьей. Связь между параллельностью прямых и их перпендикулярностью к плоскости. Признак перпендикулярности прямой и плоскости. |
| 35 | Существование и единственность прямой, проходящей через любую точку пространства перпендикулярно к данной прямой. |
| 36 | Теорема о параллельности плоскостей, перпендикулярных к данной прямой. |
| 37 | Контрольная работа № 6 |
| 38 | Перпендикуляр и наклонная. Длина перпендикуляра и длина наклонной. |
| 39 | Расстояние от точки до плоскости, расстояния между параллельными плоскостями, между прямой и параллельной ей плоскостью, между скрещивающимися прямыми |
| 40 | Теорема о трех перпендикулярах (прямая и обратная) |
| 41 – 42 | Ортогональное проектирование и его свойства. Угол между прямой и плоскостью. Теоремы о длине ортогональной проекции отрезка на плоскость и прямую. |
| 43 – 44 | Контрольная работа № 7 |
| Угол между двумя плоскостями. Перпендикулярность плоскостей (14 ч) |
| 45 | Двухгранный угол. Линейный угол двухгранного угла. |
| 46 – 48 | Перпендикулярные плоскости. Признак перпендикулярности двух плоскостей . Теорема о лежащей в одной из двух взаимно перпендикулярных плоскостей и перпендикулярной к другой плоскости. Теорема о линии пересечения двух плоскостей, каждая из которых перпендикулярна к третьей плоскости. Теорема о существовании и единственности общего перпендикуляра к двум данным скрещивающимся прямым, пересекающего каждую из них. |
| 49 – 51 | Угол между двумя плоскостями. Теорема об угле между плоскостями. Теорема о площади ортогональной проекции многоугольника. |
| 52 – 56 | Прямоугольный параллелепипед, его свойства. Куб. Прямая призма. Построение сечений, проходящих через данную точку перпендикулярно к данной прямой. Решение задач. |
| 57 – 58 | Контрольная работа № 8 |
| Многогранные углы. Многогранники (22 ч) |
| 59 – 62 | Трехгранные углы. Полярные трехгранные углы. Теорема о сумме плоских углов трехгранного и многогранного углов. Теоремы синусов и косинусов трехгранных углов. |
| 63 | Контрольная работа № 9. |
| 64 – 67 | Многогранники. Выпуклые многогранники. Формула Эйлера (может быть изложена без доказательства). Правильные многогранники, их двойственность. Элементы симметрии правильных многогранников. |
| 68 – 70 | Пирамида. Правильная пирамида. Теорема о площади боковой поверхности правильной усеченной пирамиды. |
| 71 | Теорема о площади боковой поверхности прямой и наклонной призм. |
| 72 – 74 | Прямоугольный, равногранный, ортоцентрический тетраэдры, их свойства. |
| 75 – 78 | Решение задач |
| 79 – 80 | Контрольная работа № 10 |
| Векторы и координаторы в пространстве (16 ч) |
| 81 – 82 | Вектор. Модуль вектора. Равенство векторов. Операции над векторами и их свойства. |
| 83 – 85 | Компланарные векторы. Правило параллелепипеда. Признак компланарности трех векторов. Теорема о разложении вектора по трем некомпланарным векторам. |
| 86 | Контрольная работа № 11 |
| 87 – 90 | Координаты точки и координаты вектора. Свойства векторов пространства, заданных своими координатами. Вычисление длины вектора по его координатами. Расстояние между двумя точками. Координаты точки, делящей отрезок в данном отношении. Проекция вектора на ось. |
| 91 – 94 | Скалярное произведение векторов. Скалярное произведение в координатах. Свойства скалярного произведения. Применение векторов к решению задач. |
| 95 – 96 | Контрольная работа № 12 |
| 97 – 103 | Повторение |
| 104 - 105 | Итоговая контрольная работа |
Список литературы:
Атанасян, Л.С. Геометрия [Текст]: учебник для 10-11 класса. – М.:Просвещение, 2007.
Звавич Л.И., Рязановский А.Р., Такуш Е.В. Контрольные и проыерочные работы по геометрии 10 – 11 классы – М.: Дрофа, 2001.
Звавич, Л.И. Геометрия [Текст]: пособие для школ и классов с углублённым изучением математики – М.: Дрофа, 2006. – 288 с.
Звавич, Л.И. Многогранники: развёртки и задачи: альбом для решения задач по стереометрии, часть 1-3. – М.: Дрофа, 2005.
Зив Б. Г. Геометрия. Дидактический материал 10 класс – М.: Просвещение, 2007.
Зив Б. Г. Задачи по геометрии 7 – 11классы – М.: Просвещение, 2000.
Зив, Б.Г. Задачи к урокам геометрии 7-11 классы С.-П.: НПО Семья и мир, 2008
Ковалева Г.И., Мазурова Н.И. Геометрия. Тес ты для текущего и обобщающего контроля – Волгоград: Учитель, 2009.
Потоскуев, Е.В. Геометрия 10 класс/ задачник для общеобразовательных учреждений с углублённым и профильным изучением математики – М.: Дрофа, 2005.
Потоскуев, Е.В. Геометрия 10 класс/ учебник для общеобразовательных учреждений с углублённым и профильным изучением математики – М.: Дрофа, 2005.
Рабинович Е.М. Математика. Задачи и упражнения на готовых чертежах 10 – 11 класс – М.: Илекса, 2010
Шарыгин И.Ф. Геометрия. Стереометрия 10 – 11 классы – М.: Дрофа, 1998.

 Получите свидетельство
Получите свидетельство Вход
Вход











 Программа по геометрии (углубленный уровень 10 класс) (48.01 КB)
Программа по геометрии (углубленный уровень 10 класс) (48.01 КB)
 0
0 2013
2013 152
152 Нравится
0
Нравится
0



