Муниципальное казенное общеобразовательное учреждение
средняя общеобразовательная школа № 17 р.п.Юрты
Рассмотрено Согласовано Утверждено
на заседании МО Зам.директора по УВР приказом директора
учителей МИФ МКОУ СОШ№17 МКОУ СОШ№17
МКОУ СОШ№17 __________ Кочергина И.Г. №___от_________
Протокол№___ от___ _________Цаберт И.П.
__________Пузик ИН
Рабочая программа учебного курса
по геометрии для 10 класса МКОУСОШ № 17 на 2013/2014учебный год
Разработчик: Пузик Ирина Николаевна, учитель математики, первая квалификационная категория.
2013 г., р.п.Юрты
Пояснительная записка.
Рабочая программа учебного предмета «Гометрия - 10» (далее Рабочая программа) составлена на основании следующих нормативно-правовых документов:
Закон 273-ФЗ «Об образовании в РФ»;
Федеральный компонент государственного образовательного стандарта, утвержденный Приказом Минобразования РФ от 05 03 2004 года № 1089;
Федеральный государственный образовательный стандарт основного общего образования;
Сборника рабочих программ по геометрии для 10-11 классов (составитель: Т.А.Бурмистрова ), Москва «Просвещение» 2009год.
Программа соответствует учебнику «Геометрия 10-11» для десятого класса образовательных учреждений (Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев и другие, Москва «Просвещение» 2011 г.) и обеспечена учебно-методическим комплектом «Геометрия - 10».
Перечень компонентов учебно-методического комплекса, обеспечивающего реализацию рабочей программы:
- базовый учебник;
- дополнительная литература для учителя и учащихся;
- перечень Интернет-ресурсов и других электронных информационных источников, обучающих, справочно-информационнных, контролирующих компьютерных программ.
Содержание программы направлено на освоение учащимися знаний, умений и навыков на базовом уровне, что соответствует Образовательной программе школы. Она включает все темы, предусмотренные федеральным компонентом государственного образовательного стандарта основного общего образования по математике и авторской программой учебного курса.
Преобладающей формой текущего контроля служат:
- письменные опросы: контрольные, самостоятельные работы, тесты;
- устные опросы: собеседование, зачеты.
Список используемой литературы:
Газеты «Математика» приложение к 1 сентября.
Атанасян, Л. С. Геометрия: учебник для 10-11 кл. общеобразовательных учреждений / Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев и др. - М.: Просвещение, 2011.
Зив, Б. Г. Дидактические материалы по геометрии для 10 кл. [Текст] / Б. Г. Зив. - М.: Просвещение, 2000.
Дополнительная литература:
Денищева, А. О. Единый государственный экзамен. Математика: 2004-2005 / контрольные измерительные материалы. Министерство образования и науки Российской Федерации, Федеральная служба по надзору в сфере образования и науки [Текст] / А. О. Денищева, П. К. Безрукова, Е. М. Бойченко и др. / под ред. Г. С. Ковалёвой. - М.: Просвещение, 2005.
Евдокимова, К Н. Геометрия в таблицах и схемах [Текст] / Н. Н. Евдокимова. - СПб.: Изд. дом «Литера», 2005.
Единый государственный экзамен. Математика. Учебно-тренировочные тесты-2005 [Текст]. - Ростов н/Д.: Легион, 2005.
Место курса в учебном плане.
Базисный учебный (образовательный) план на изучение алгебры в основной школе отводит 2часа в неделю в течение каждого года обучения, всего 70часов.
Количество часов по плану:
всего 70ч( в неделю – 2ч), контрольных работ- 5.
Изучение математики на базовом уровне среднего (полного) общего образования направлено на достижение следующих целей:
развитие логического мышления, пространственного воображения и интуиции, критичности мышления на уровне, необходимом для продолжения образования и самостоятельной деятельности в области математики и ее производных, в будущей профессиональной деятельности;
воспитание средствами геометрии культуры личности: отношения к математике как части общечеловеческой культуры.
Задачи курса геометрии для достижения поставленных целей:
систематическое изучение свойств геометрических тел в пространстве;
формирование умения применять полученные знания для решения практических задач, проводить доказательные рассуждения, логически обосновывать выводы для изучения школьных естественнонаучных дисциплин на базовом уровне.
Планируемые результаты изучения курса геометрии в 10 классе.
В ходе освоения содержания математического образования учащиеся овладевают разнообразными способами деятельности, приобретают и совершенствуют опыт:
построения и исследования математических моделей для описания и решения прикладных задач, задач из смежных дисциплин;
выполнения и самостоятельного составления алгоритмических предписаний и инструкций на математическом материале;
выполнения расчетов практического характера использования математических формул и самостоятельного составления формул на основе обобщения частных случаев и эксперимента;
самостоятельной работы с источниками информации, обобщения и систематизации полученной информации, интегрирования ее в личный опыт;
проведения доказательных рассуждений, логического обоснования выводов, различения доказанных и недоказанных утверждений, аргументированных и эмоционально убедительных суждений;
самостоятельной и коллективной деятельности, включения своих результатов в результаты работы группы, соотнесения своего мнения с мнением других участников учебного коллектива и мнением авторитетных источников.
Результаты обучения представлены в Требованиях к уровню подготовки и задают систему итоговых результатов обучения, которых должны достигать все учащиеся, оканчивающие среднюю школу, и достижение которых является обязательным условием положительной аттестации ученика за курс средней школы. Эти требования структурированы по трем компонентам: «знать/понимать», «уметь», «использовать приобретенные знания и умения в практической деятельности и повседневной жизни». При этом последние два компонента представлены отдельно по каждому из разделов содержания.
Очерченные стандартом рамки содержания и требований ориентированы на развитие учащихся и не должны препятствовать достижению более высоких уровней.
Формы контроля:
Срезовые работы: входной контроль, промежуточный контроль, итоговый контроль;
текущий контроль (письменные опросы): контрольные работы, тесты, самостоятельные работы;
текущий контроль (устные опросы): собеседование, зачеты;
медиаформы: индивидуальные тесты Excel, фронтальные тесты PowerPoint.
|
| I четверть (9 недель) | II четверть (7 недель) | III четверть (10 недель) | IV четверть (8 недель) | Учебный год (35 недель) |
|
| Учебных часов | 18 | 14 | 20 | 16 | 70 |
| контрольных работ | 1 | 1 | 2 | 1 | 5 |
| практических работ |
| 2 | 2 |
| 4 |
|
Требования к уровню подготовки учащихся.
Уметь:
распознавать на чертежах и моделях пространственные формы;
соотносить трехмерные объекты с их описаниями, изображениями;
описывать взаимное расположение прямых и плоскостей в пространстве, аргументировать свои суждения об этом расположении;
анализировать в простейших случаях взаимное расположение объектов в пространстве;
изображать основные многогранники; выполнять чертежи по условиям задач;
строить простейшие сечения куба, призмы, пирамиды;
решать планиметрические и простейшие стереометрические задачи на нахождение геометрических величин (длин, углов, площадей);
использовать при решении стереометрических задач планиметрические факты и методы;
проводить доказательные рассуждения в ходе решения задач.
Использовать приобретенные знания и умения в практической деятельности и повседневной жизни:
для исследования (моделирования)несложных практических ситуаций на основе изученных формул и свойств фигур;
для вычисления площадей поверхностей пространственных тел при решении практических задач, используя при необходимости справочники и вычислительные устройства.
Изменения в программе.
В учебнике «Геометрия. 10-11 классы» под редакцией Л. С. Атанасяна отсутствует тема «Параллельное проектирование». Эта тема является важной при изучении стереометрии и указана в основном содержании Примерной программы. Изучение темы включено в рабочую программу в раздел «Параллельность прямых и плоскостей» как тема отдельного урока. Материал для изучения темы «Параллельное проектирование» необходимо взять из Приложения к учебнику.
Тема «Некоторые сведения из планиметрии», предусмотрена для изучения на профильном уровне, вместо высвободившихся часов тему «Вектору» переношу в 10 класс.
В связи с тем, что в учебном году 35 недель, а примерная программа в 10 классе по геометрии рассчитана на 68 часов, добавляю 2 часа на повторение в конце года.
Календарно тематическое планирование.
| № | Содержание учебного материала | Кол-во часов | Характеристика деятельности обучающихся | Дата |
| по плану | факт |
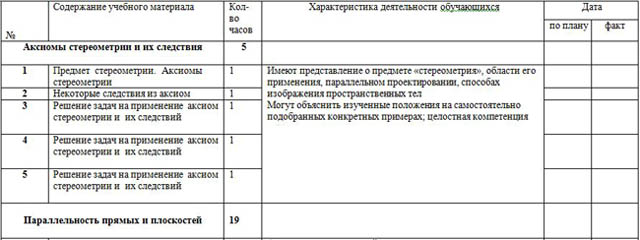
| Аксиомы стереометрии и их следствия
| 5
|
|
|
|
| 1 | Предмет стереометрии. Аксиомы стереометрии | 1 | Имеют представление о предмете «стереометрия», области его применения, параллельном проектировании, способах изображения пространственных тел Могут объяснить изученные положения на самостоятельно подобранных конкретных примерах; целостная компетенция |
|
|
| 2 | Некоторые следствия из аксиом | 1 |
|
|
| 3 | Решение задач на применение аксиом стереометрии и их следствий
| 1 |
|
|
| 4 | Решение задач на применение аксиом стереометрии и их следствий
| 1 |
|
|
| 5 | Решение задач на применение аксиом стереометрии и их следствий
| 1 |
|
|
|
Параллельность прямых и плоскостей
|
19 |
|
|
|
| 6 | Параллельные прямые в пространстве | 1 | Анализировать в простейших случаях расположение прямых в пространстве, используя определение параллельных прямых, описывать взаимное расположение прямой и плоскости в пространстве, применять признак при доказательстве параллельности прямой и плоскости, распознавать на чертежах и моделях скрещивающиеся прямые, Иметь представление об углах между пересекающимися, параллельными и скрещивающимися прямыми в пространстве, находить угол между прямыми в пространстве на модели куба. решать простейшие стереометрические задачи на нахождение углов между прямыми, находить на моделях параллелепипеда параллельные, скрещивающиеся и пересекающиеся прямые, определять взаимное расположение прямой и плоскости, решать задачи на доказательство параллельности плоскостей с помощью признака параллельности плоскостей применять признак и свойства при решении задач Уметь: распознавать на чертежах и моделях параллелепипед и тетраэдр и изображать на плоскости, строить сечение плоскостью, параллельной граням параллелепипеда, тетраэдра; строить диагональные сечения в параллелепипеде, тетраэдре; сечения плоскостью, проходящей через ребро и вершину параллелепипеда, строить сечения параллелепипеда и тетраэдра плоскостью, параллельной грани; применять свойства параллельных прямой и плоскости, параллельных плоскостей при доказательстве подобия треугольников в пространстве, для нахождения стороны одного из треугольников.
|
|
|
| 7 | Параллельность прямой и плоскости | 1 |
|
|
| 8 | Решение задач | 1 |
|
|
| 9 | Решение задач | 1 |
|
|
| 10 | Решение задач | 1 |
|
|
| 11 | Скрещивающиеся прямые |
|
|
|
| 12 | Углы с сонаправленными сторонами | 1 |
|
|
| 13 | Решение задач | 1 |
|
|
| 14 | Решение задач | 1 |
|
|
| 15 | КР№1 | 1 |
|
|
| 16 | Параллельные плоскости. | 1 |
|
|
| 17 | Свойства параллельных плоскостей | 1 |
|
|
| 18 | Тетраэдр | 1 |
|
|
| 19 | Параллелепипед | 1 |
|
|
| 20 | Задачи на построение сечений | 1 |
|
|
| 21 | Задачи на построение сечений | 1 |
|
|
| 22 | Закрепление свойств параллелепипеда | 1 |
|
|
| 23 | КР№2 | 1 |
|
|
| 24 | Зачет№1 | 1 |
|
|
|
Перпендикулярность прямых и плоскостей
| 20 |
|
|
|
| 25 | Перпендикулярные прямые в пространстве. Параллельные прямые . перпендикулярные к плоскости | 1 | Знают определение перпендикулярных прямых в пространстве, перпендикулярных прямой и плоскости; формулировки основных теорем о перпендикулярности прямых, прямой и плоскости. Умеют доказывать изученные теоремы, применять их для решения простейших задач на доказательство .Могут объяснить изученные положения на самостоятельно подобранных конкретных примерах; предметная компетенция Имеют представление об ортогональном проектировании. Умеют решать задачи, используя ортогональное проектирование. Могут составить план выполнения построений, привести примеры, сформулировать выводы; предметная компетенция. Знают определение перпендикуляра, наклонной, угла между прямой и плоскостью, формулировку теоремы о трёх перпендикулярах. Умеют применять полученные знания при решении типовых задач. Могут объяснить изученные положения на самостоятельно подобранных конкретных примерах; предметная компетенция Умеют решать задачи на нахождение расстояния от точки до плоскости, угла между прямой и плоскостью.Могут работать с чертежными инструментами; предметная компетенция |
|
|
|
26 | Признак перпендикулярности прямой и плоскости | 1 |
|
|
|
27 | Теорема о прямой, перпендикулярной к плоскости | 1 |
|
|
| 28 | Решение задач | 1 |
|
|
| 29 | Решение задач | 1 |
|
|
| 30 | Административная КР | 1 |
|
|
|
31
| Расстояние от точки до плоскости. Теорема о трех перпендикулярах | 1 |
|
|
| 32 | Угол между прямой и плоскостью | 1 |
|
|
| 33 | Решение задач | 1 |
|
|
| 34 | Решение задач | 1 |
|
|
| 35 | Решение задач |
|
|
|
| 36 | Угол между прямой и плоскостью (повторение) | 1 |
|
|
| 37 | Двугранный угол | 1 |
|
|
| 38 | Признак перпендикулярности двух плоскостей | 1 |
|
|
| 39 | Прямоугольный параллелепипед | 1 |
|
|
| 40 | Решение задач | 1 |
|
|
|
41 | Перпендикулярность прямых и плоскостей (повторение) | 1 |
|
|
| 42 | Решение задач | 1 |
|
|
| 43 | К.Р№3 | 1 |
|
|
| 44 | Зачет№2 | 1 |
|
|
|
Многогранники
| 12 |
|
|
|
| 45 | Понятие многогранника | 1 | Знают теорему Эйлера, пространственную теорему Пифагора. Умеют применять изученные теоремы при решении типовых задач. Осуществляют проверку выводов, положений, закономерностей, теорем; предметная компетенция Умеют решать задачи на применение формул для вычисления площади призмы. Могут воспроизвести теорию с заданной степенью свернутости; целостная компетенция .Умеют решать задачи на применение формул для вычисления площади пирамиды. Могут воспроизвести теорию с заданной степенью свернутости; целостная компетенция. Умеют четко различать виды многогранников. Знают характерные свойства многогранников. Умеют изображать их на чертежах и решать задачи с многогранниками, изготовлять бумажные модели многогранников по их разверткам. Могут воспроизводить изученные правила и понятия, подбирать аргументы, соответствующие решению; предметная компетенция. |
|
|
|
46 | Призма. Площадь поверхности призмы. | 1 |
|
|
| 47 | Решение задач | 1 |
|
|
| 48 | Решение задач | 1 |
|
|
| 49 | Пирамида | 1 |
|
|
| 50 | Правильная пирамида | 1 |
|
|
| 51 | Решение задач | 1 |
|
|
| 52 | Решение задач |
|
|
|
| 53 | Усечённая пирамида. Площадь поверхности усечённой пирамиды | 1 |
|
|
| 54 | Симметрия в пространстве. Понятие правильного многогранника | 1 |
|
|
| 55 | КР№4 | 1 |
|
|
| 56 | Зачёт №3 | 1 |
|
|
|
Векторы в пространстве | 6 | Знают определение вектора, способ его изображения и названия. Умеют строить вектор, распознавать равные векторы. Осуществляют проверку выводов, положений, закономерностей, теорем; предметная компетенция .Знают правила нахождения суммы и разности векторов. Умеют решать задачи повышенной сложности на применение изученных правил. Умеют аргументированно отвечать на поставленные вопросы, могут осмыслить ошибки и их устранить; целостная компетенция. Умеют применять векторный метод при решении геометрических задач, прослеживать связь между элементами многогранников и векторами в пространстве. Умеют аргументированно отвечать на поставленные вопросы, могут осмыслить ошибки и их устранить; целостная компетенция Учащиеся демонстрируют теоретические знания по теме. Могут свободно излагать теоретический материал и решать задачи.Умеют аргументированно отвечать на поставленные вопросы, могут осмыслить ошибки и их устранить; целостная компетенция |
|
|
| 57 | Понятие вектора. Равенство векторов | 1 |
|
|
| 58 | Сложение и вычитание векторов. Сумма нескольких векторов | 1 |
|
|
| 59 | Умножение вектора на число | 1 |
|
|
| 60 | Компланарные векторы. Правило параллелепипеда | 1 |
|
|
|
61 | Разложение вектора по трём некомпланарным векторам | 1 |
|
|
| 62 | Зачёт№4 | 1
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Повторение | 8 |
|
|
|
| 63 | Аксиомы стереометрии и их следствия | 1 |
|
|
|
| 64 | Параллельность прямых и плоскостей | 1 |
|
|
|
65 | Теорема о трех перпендикулярах. Угол между прямой и плоскостью | 1 |
|
|
| 66 | КР№5 | 1 |
|
|
| 67 | Векторы в пространстве | 1 |
|
|
| 68 | Решение задач | 1 |
|
|
| 69 | Решение задач | 1 |
|
|
| 70 | Обобщающий урок | 1 |
|
|

 Получите свидетельство
Получите свидетельство Вход
Вход











 Рабочая программа по геометрии (10 класс) (34.59 КB)
Рабочая программа по геометрии (10 класс) (34.59 КB)
 0
0 2443
2443 594
594 Нравится
0
Нравится
0




