Свойство биссектрисы угла треугольника

Цель урока:

Познакомиться со свойством биссектрисы  угла треугольника и отработать его применение при решении задач.

Теорема:

Биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные двум другим сторонам.

Доказательство - смотри презентацию

№1. Биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные двум другим сторонам.

Дополнительные вопросы:

Укажи верные утверждения

а)  Любые два параллелограмма подобны.

б)  Любые два прямоугольника подобны.

в)  Любые две окружности подобны.

Укажите верные утверждения

а)  Любые два ромба подобны.

б)  Любые два квадрата подобны.

в)  Любые две трапеции подобны.

Презентация содержит 20 слайдов.

Урок

геометрии

Сентябрь 2002г.

9 класс

Учитель

Козина Н.А.

• Практическая работа в «Живой

Геометрии».

• Доказательство свойства

биссектрисы угла треугольника.

• Решение задач.

Познакомиться со свойством биссектрисы угла треугольника и отработать его применение при решении задач.

Биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные двум другим сторонам.

C

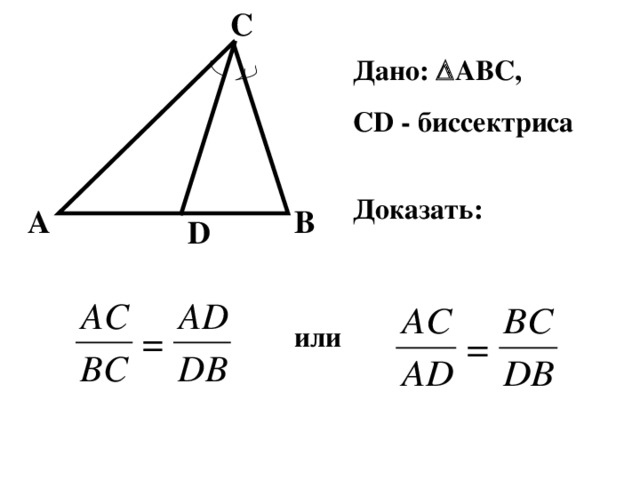
Дано :  ABC,

CD - биссектриса

Доказать :

A

B

D

или

С

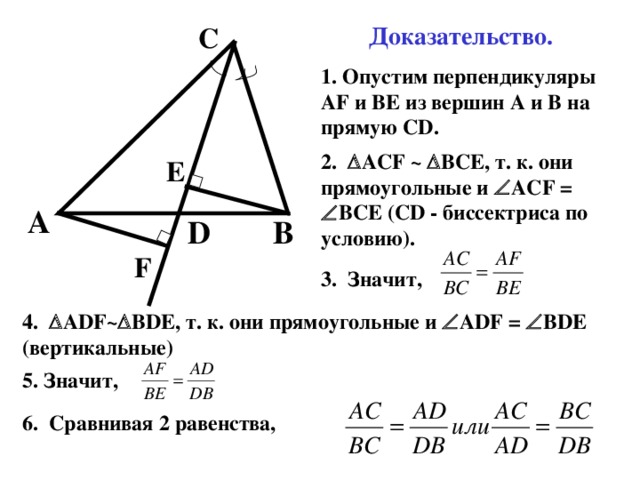
Доказательство.

1. Опустим перпендикуляры AF и BЕ из вершин A и B на прямую CD .

2.  ACF ~  BCE, т. к. они прямоугольные и  ACF =  BCE (CD - биссектриса по условию).

Е

A

D

B

F

3. Значит,

4.  ADF~  BDE, т. к. они прямоугольные и  ADF =  BDE ( вертикальные)

5. Значит,

6. Сравнивая 2 равенства, получаем

N

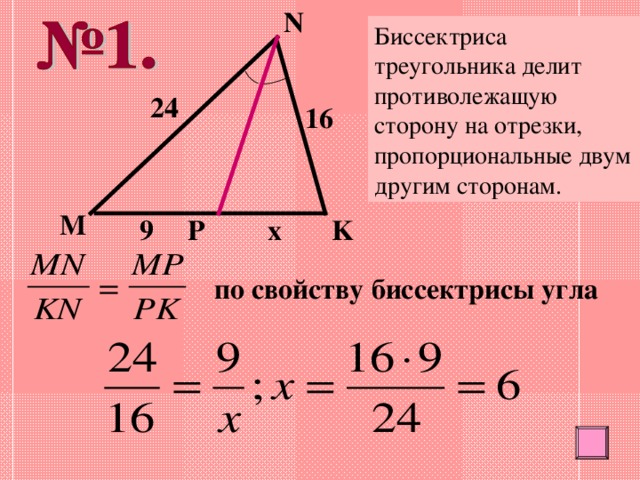
Биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные двум другим сторонам.

24

16

M

K

P

9

x

по свойству биссектрисы угла

B

8

22

12

O

D

C

x

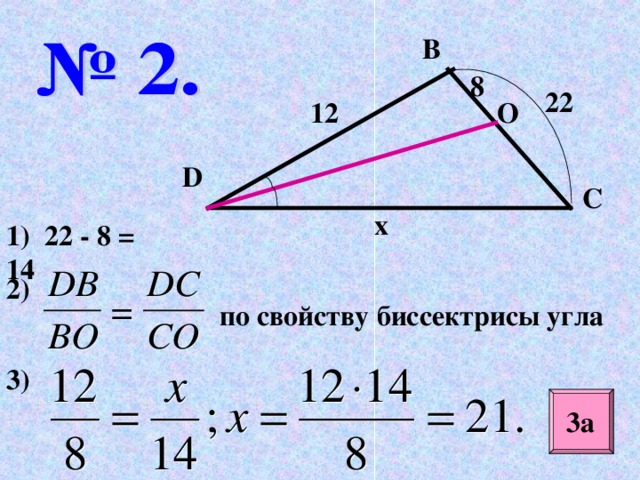
1) 22 - 8 = 14

2)

по свойству биссектрисы угла

3)

3а

7

1

2

3

5

4

6

№ 2

№ 3а

№ 3б

Д.з.

Укажи верные утверждения

а) Любые два параллелограмма подобны.

б) Любые два прямоугольника подобны.

в) Любые две окружности подобны.

Укажите верные утверждения

а) Любые два ромба подобны.

б) Любые два квадрата подобны.

в) Любые две трапеции подобны.

B

3

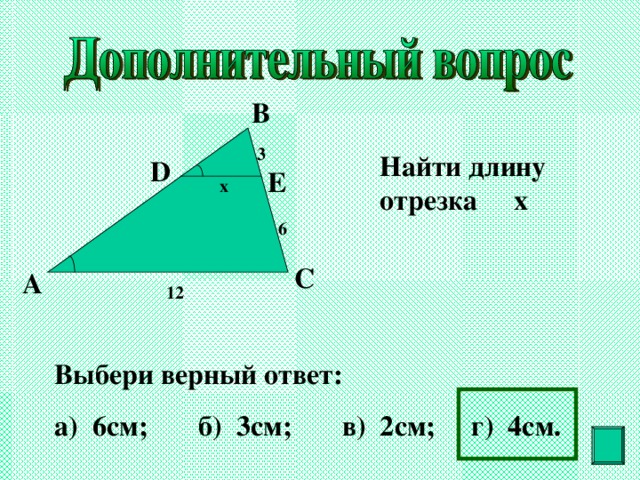
Найти длину отрезка x

D

E

x

6

C

A

12

Выбери верный ответ :

а) 6см ; б) 3см ; в) 2см ; г) 4см.

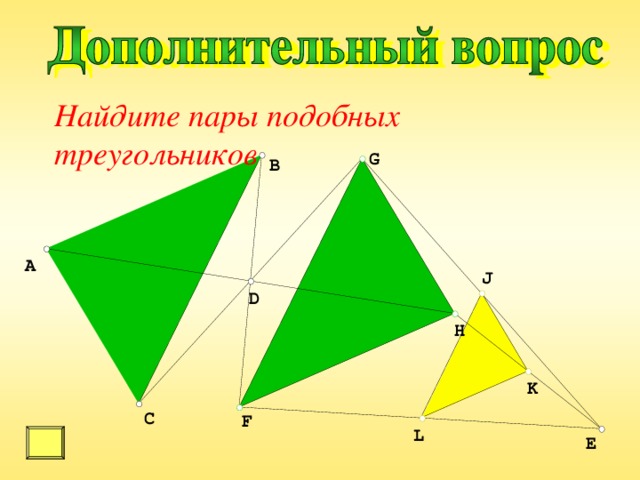
Найдите пары подобных треугольников

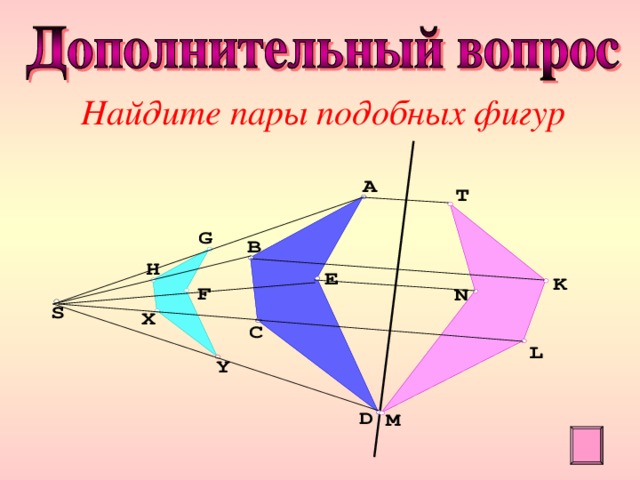
Найдите пары подобных фигур

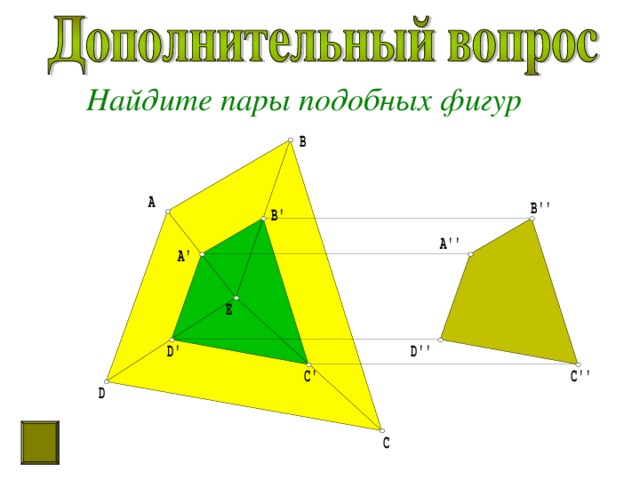
Найдите пары подобных фигур

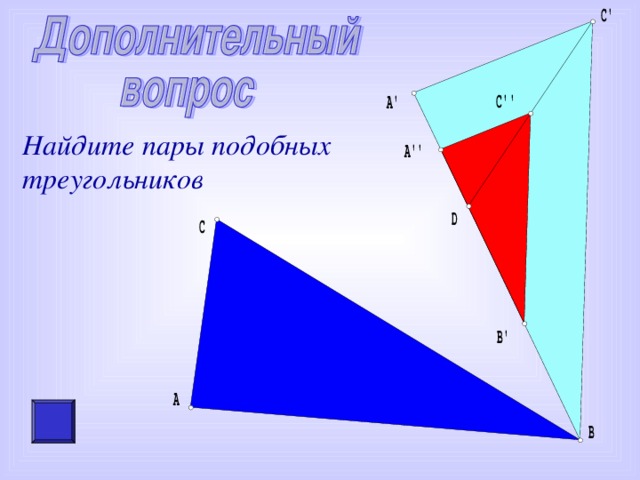
Найдите пары подобных треугольников

В

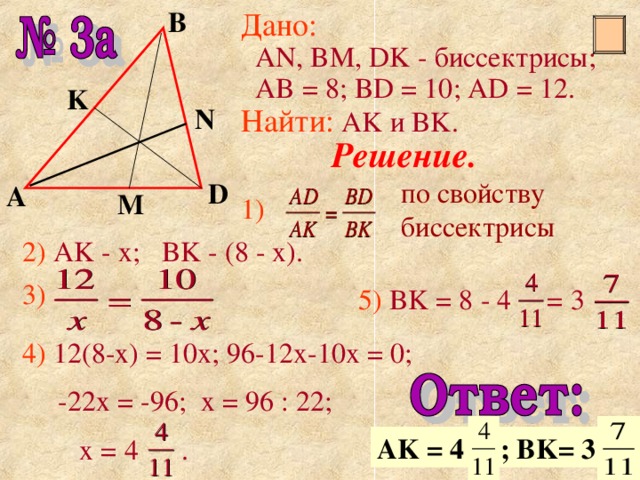
Дано :

AN, BM, DK - биссектрисы;

AB = 8; BD = 10; AD = 12 .

Найти : AK и BK.

K

N

Решение.

по свойству биссектрисы

D

А

M

1)

2) AK - x; BK - (8 - x).

3)

5) BK = 8 - 4 = 3

4) 12(8-x) = 10x; 96-12x-10x = 0;

-22x = -96; x = 96 : 22;

x = 4 .

AK = 4 ; BK= 3

В

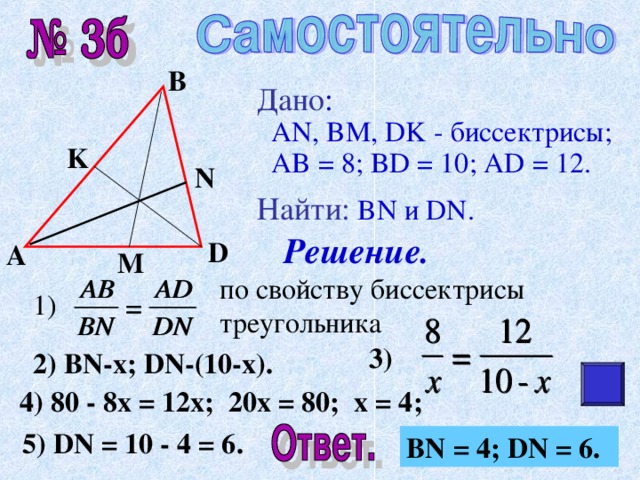
Дано :

AN, BM, DK - биссектрисы;

AB = 8; BD = 10; AD = 12 .

Найти : BN и DN.

K

N

Решение.

D

А

M

по свойству биссектрисы треугольника

1)

3)

2) BN-x; DN-(10-x).

4) 80 - 8x = 12x; 20x = 80; x = 4;

5) DN = 10 - 4 = 6.

BN = 4; DN = 6.

Учить теорему с доказательством.

№ 3. Найти AM и DM .

Повторить признаки подобия треугольников.