Свойства параллельных плоскостей

Презентация может использоваться на уроке геометрии в10  кл (уч. Атанасян Л.С." Геометрия  10-11"), на слайдах представлены задачи, в которых раскрываются некоторые свойства, разбирается их доказательство. Её можно использовать и при работе с другим учебником, не обращая внимание на нумерацию задач.

Если две параллельные плоскости пересечены третьей, то линии пересечения плоскостей параллельны.

Отрезки параллельных прямых, заключённые между параллельными плоскостями, равны.

Если прямая пересекает плоскость α, то она пересекает и любую плоскость, параллельную α.

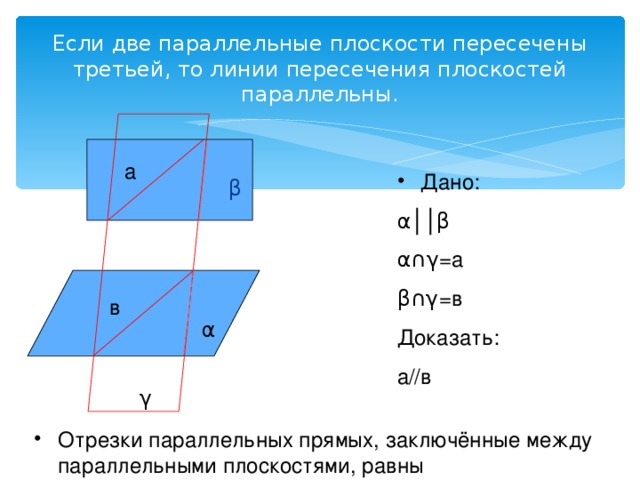
Если две параллельные плоскости пересечены третьей, то линии пересечения плоскостей параллельны.

β

а

• Дано:

α││β

α∩γ = а

β∩γ = в

Доказать:

а//в

α

в

γ

• Отрезки параллельных прямых, заключённые между параллельными плоскостями, равны

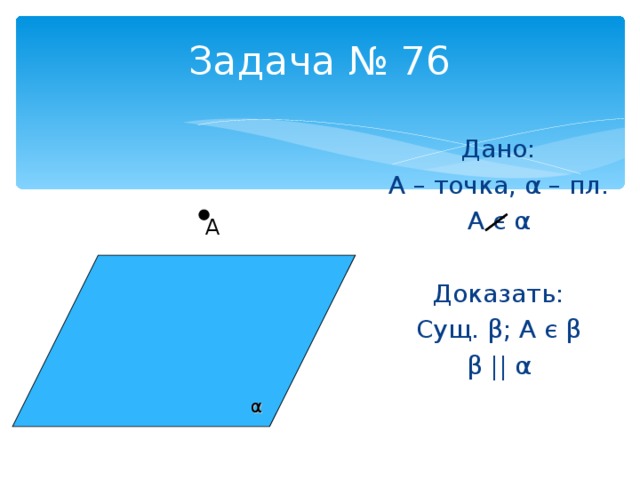
Задача № 76

Дано:

A – точка , α – пл.

A є α

Доказать:

Сущ. β ; A є β

β || α

A

α

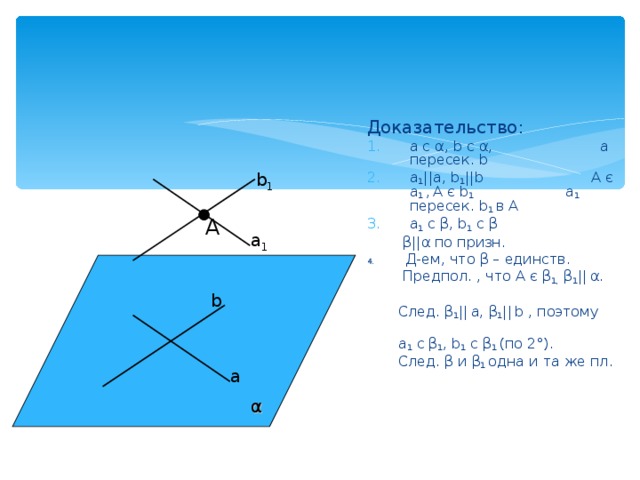
Доказательство:

• a c α , b c α , a пересек. b
• a 1 ||a, b 1 ||b A є a 1 , A є b 1 a 1 пересек. b 1 в A
• a 1 c β , b 1 c β

β || α по призн.

4. Д-ем, что β – единств.

Предпол. , что A є β 1, β 1 || α .

След. β 1 || a, β 1 || b , поэтому

a 1 c β 1 , b 1 c β 1 ( по 2 °) .

След. β и β 1 одна и та же пл.

b 1

A

a 1

b

a

α

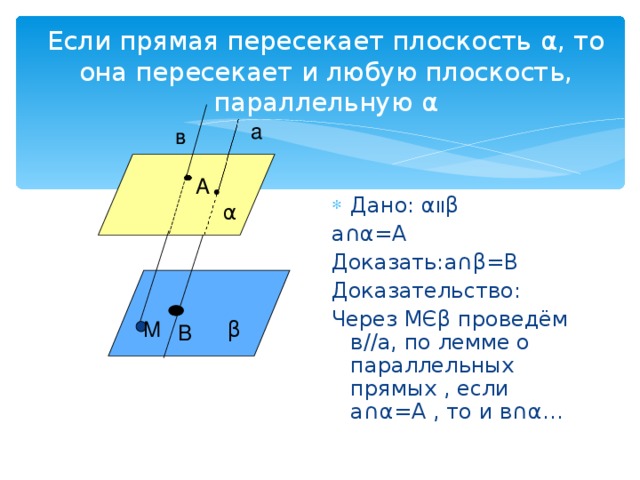
Если прямая пересекает плоскость α , то она пересекает и любую плоскость, параллельную α

а

в

α

А

• Дано: α װ β

а∩ α =A

Доказать:а∩ β =B

Доказательство:

Через МЄ β проведём в//а, по лемме о параллельных прямых , если а∩ α =A , то и в∩ α …

β

М

В

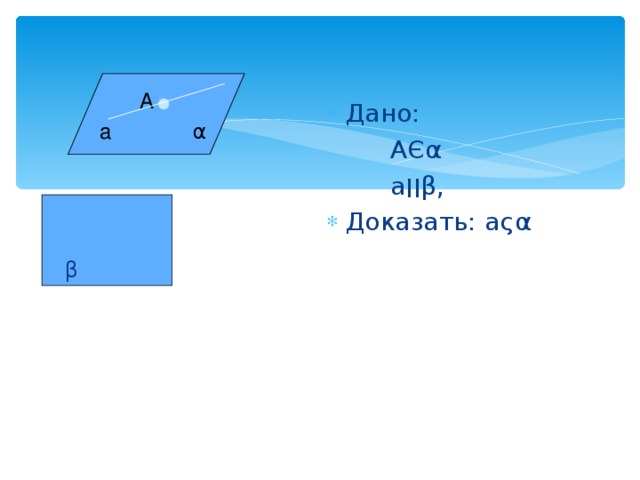
α

А

• Дано:

A Є α

а ׀׀ β,

• Доказать: а ςα

а

β

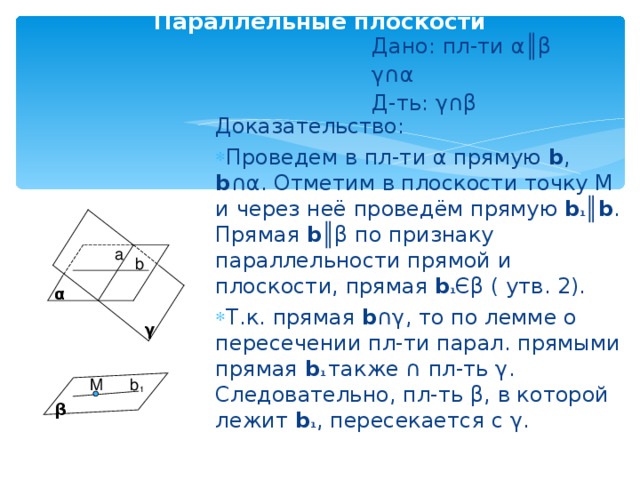
Параллельные плоскости

Дано: пл-ти α║β

γ∩α

Д-ть: γ ∩ β

Доказательство:

• Проведем в пл-ти α прямую b , b ∩ α . Отметим в плоскости точку М и через неё проведём прямую b 1 ║ b . Прямая b ║ β по признаку параллельности прямой и плоскости, прямая b 1 Є β ( утв. 2).
• Т.к. прямая b ∩ γ , то по лемме о пересечении пл-ти парал. прямыми прямая b 1 также ∩ пл-ть γ . Следовательно, пл-ть β , в которой лежит b 1 , пересекается с γ .

a

b

α

γ

b

M

1

β

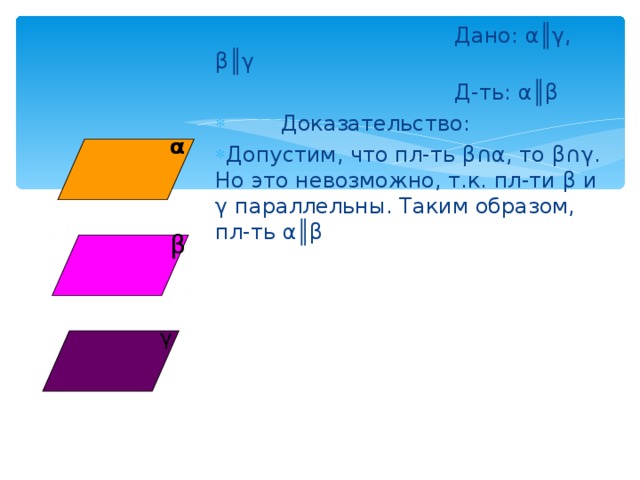
Дано: α║γ , β║γ

Д-ть: α║β

• Доказательство:
• Допустим, что пл-ть β∩α , то β∩γ . Но это невозможно, т.к. пл-ти β и γ параллельны. Таким образом, пл-ть α║β

α

β

γ

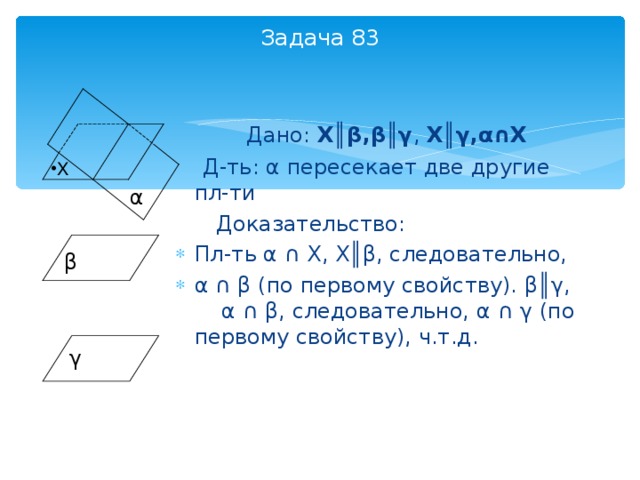
Задача 83

Дано: X║ β , β ║ γ , X ║ γ , α∩ X

Д-ть: α пересекает две другие пл-ти

Доказательство:

• Пл-ть α ∩ X , X║ β , следовательно,
• α ∩ β (по первому свойству). β║γ , α ∩ β , следовательно, α ∩ γ (по первому свойству), ч.т.д.

• X
• X

α

β

γ

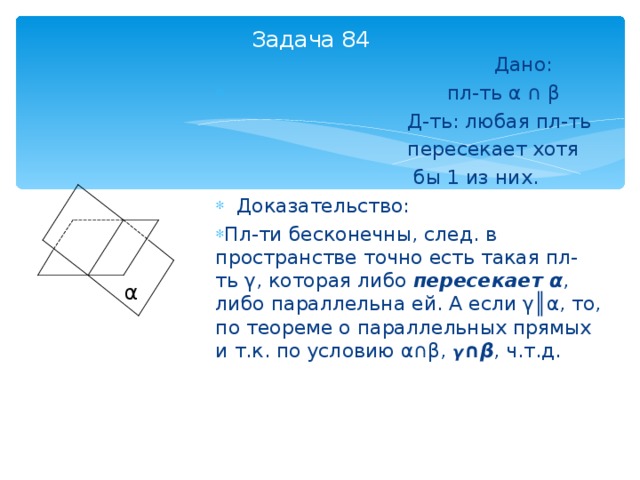
Задача 84

Дано:

• пл-ть α ∩ β

Д-ть: любая пл-ть

пересекает хотя

бы 1 из них.

• Доказательство:
• Пл-ти бесконечны, след. в пространстве точно есть такая пл-ть γ , которая либо пересекает α , либо параллельна ей. А если γ║α , то, по теореме о параллельных прямых и т.к. по условию α∩β , γ ∩β , ч.т.д.

α