Урок-презентация.
Построить сечение многогранника плоскостью – это значит указать точки пересечения секущей плоскости с ребрами многогранника и соединить эти точки отрезками, принадлежащими граням многогранника.
Для построения сечения многогранника плоскостью нужно в плоскости каждой грани указать 2 точки, принадлежащие сечению, соединить их прямой и найти точки пересечения этой прямой с ребрами многогранника.
Справочное пособие по методам решения задач по математике для средней школы. Цыпкин А.Г,.Пинский А.И./Под. редакцией В.И.Благодатских . – М.: Наука. Главная редакция физико-математической литературы, 1983. – 416 с.
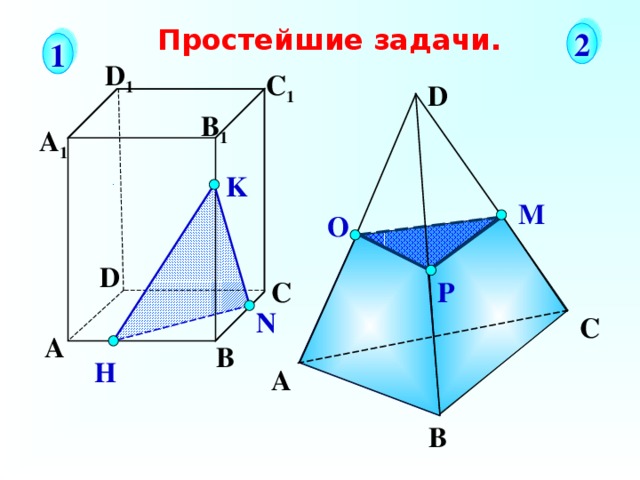
Простейшие задачи.
2
1
D 1
С 1
D
B 1
А 1
K
М
О
D
С
Р
N
Соединяем отрезками 2 точки, принадлежащие одной грани многогранника. Если у пирамиды «срезать» его вершину получится усеченная пирамида.
С
А
В
H
А
В
3
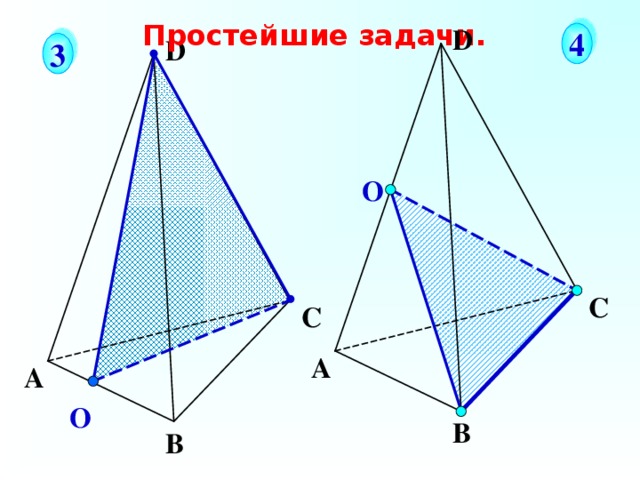
Простейшие задачи.
D
4
D
3
О
С
С
Соединяем отрезками 2 точки, принадлежащие одной грани многогранника. Диагональные сечения.
А
А
О
В
В
4
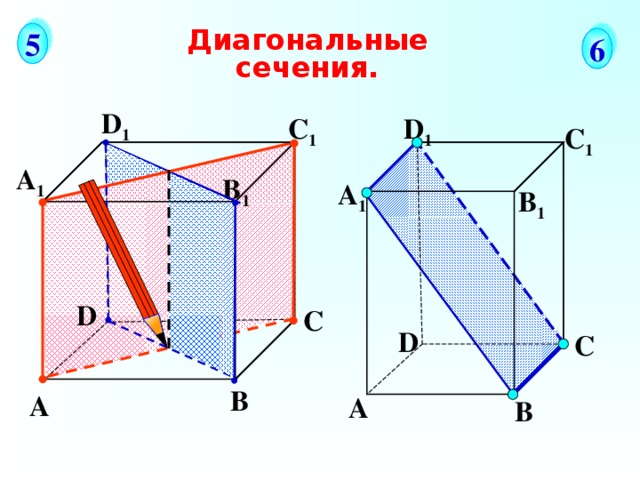
Диагональные сечения.
5
6
D 1
С 1
D 1
С 1
А 1
B 1
А 1
B 1
D
С
Соединяем отрезками 2 точки, принадлежащие одной грани многогранника. Диагональные сечения.
D
С
В
А
А
В
5
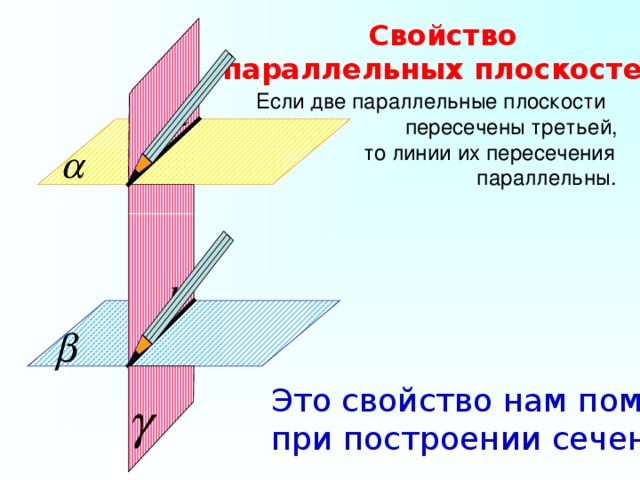
Свойство
параллельных плоскостей.
Если две параллельные плоскости
пересечены третьей,
то линии их пересечения
параллельны.
а
b
Это свойство нам поможет
при построении сечений.
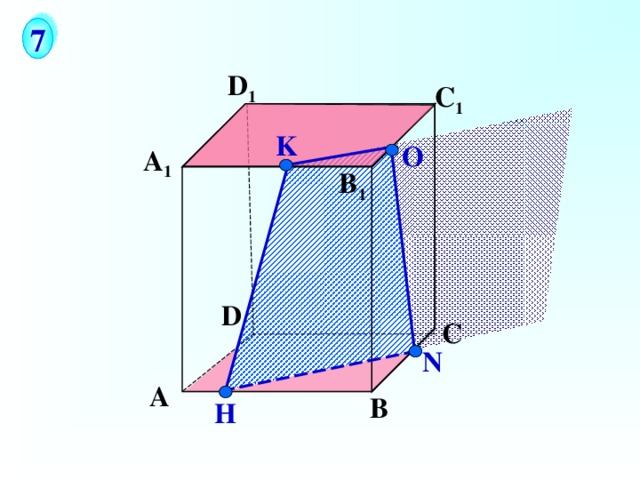
7
D 1
С 1
K
О
А 1
B 1
D
С
N
А
В
H
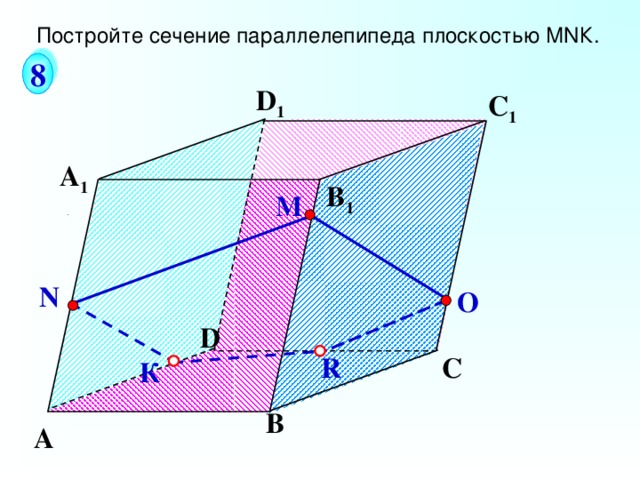
Постройте сечение параллелепипеда плоскостью М N К.
8
D 1
С 1
А 1
B 1
М
N
О
Геометрия Л.С.Атанасян, 10-11. Задача № 87(a) .
D
С
R
К
В
А
7
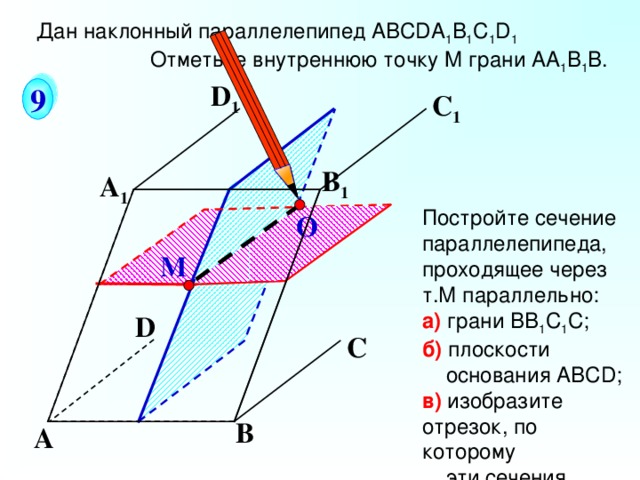
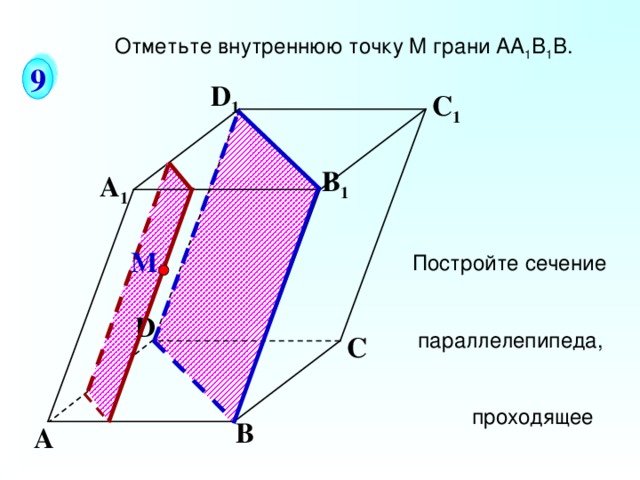
Дан наклонный параллелепипед АВС D А 1 В 1 С 1 D 1
Отметьте внутреннюю точку M грани АА 1 В 1 В.
D 1
9
С 1
Постройте сечение параллелепипеда, проходящее через т.М параллельно:
а) грани ВВ 1 С 1 С;
б) плоскости
основания АВС D ;
в) изобразите
отрезок, по которому
эти сечения
пересекаются.
B 1
А 1
О
М
Геометрия Л.С.Атанасян, 10-11. Задача № 82(а,б, в). Дан наклонный параллелепипед АВСDА1В1С1D1
Отметьте внутреннюю точку M грани АА1В1В.
Постройте сечение параллелепипеда, проходящее через т.М параллельно:
а) грани ВВ1С1С;
б) плоскости основания АВСD;
в) изобразите отрезок, по которому эти сечения пересекаются.
г) плоскости ВDD1
D
С
В
А
9
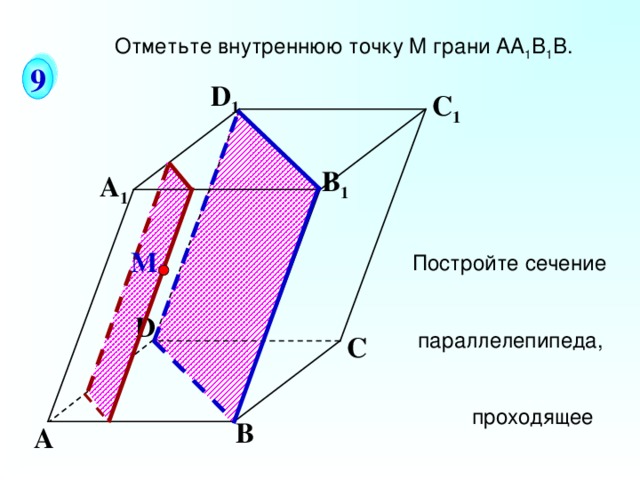
Отметьте внутреннюю точку M грани АА 1 В 1 В.
9
D 1
С 1
B 1
А 1
Постройте сечение параллелепипеда, проходящее через т.М параллельно:
г) плоскости В DD 1
М
Геометрия Л.С.Атанасян, 10-11. Задача № 82(в).
D
С
В
А
9
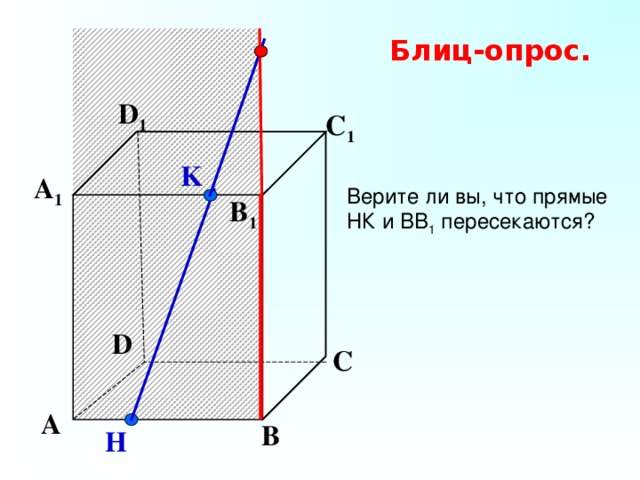
Блиц-опрос.
D 1
С 1
K
Верите ли вы, что прямые НК и ВВ 1 пересекаются?
А 1
B 1
D
С
А
В
H
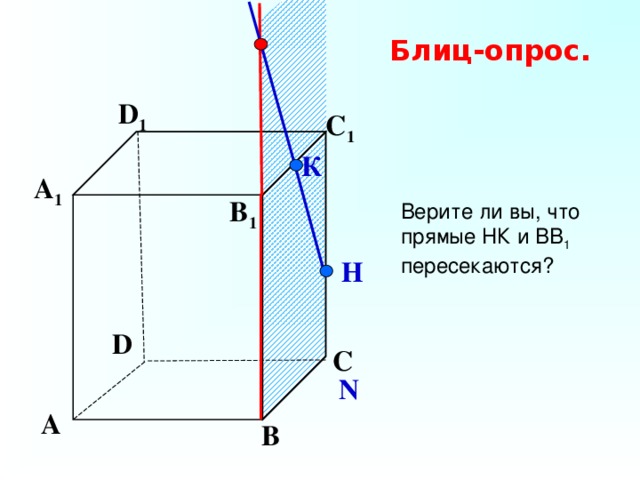
Блиц-опрос.
D 1
С 1
К
А 1
Верите ли вы, что
прямые НК и ВВ 1
пересекаются?
B 1
Н
D
С
N
А
В
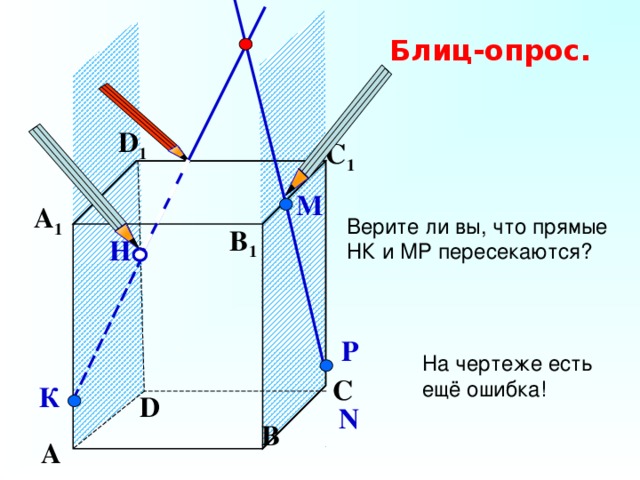
Блиц-опрос.
D 1
С 1
М
Верите ли вы, что прямые НК и МР пересекаются?
А 1
B 1
Н
Р
На чертеже есть
ещё ошибка!
С
К
D
N
В
А
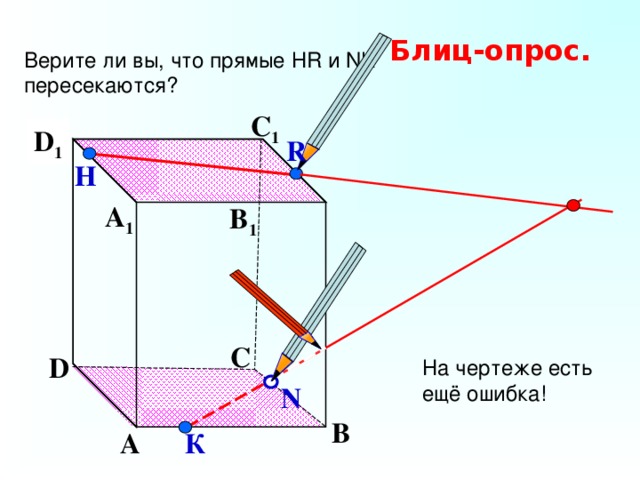
Верите ли вы, что прямые Н R и NK
пересекаются?
Блиц-опрос.
С 1
D 1
R
Н
А 1
B 1
С
D
На чертеже есть
ещё ошибка!
N
В
А
К
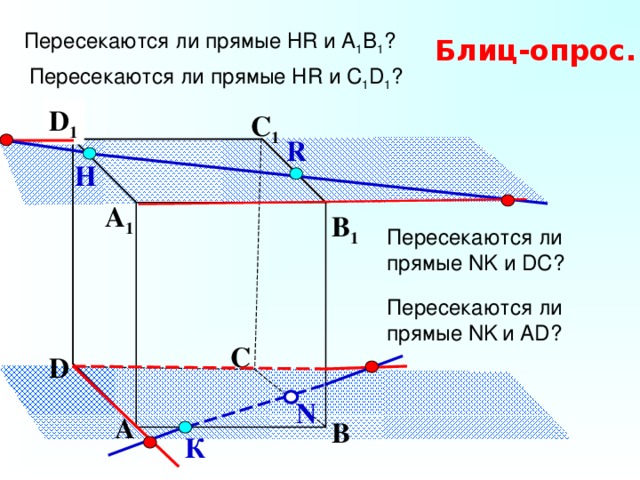
Пересекаются ли прямые Н R и А 1 В 1 ?
Блиц-опрос.
Пересекаются ли прямые Н R и С 1 D 1 ?
D 1
С 1
R
Н
А 1
B 1
Пересекаются ли
прямые NK и DC ?
Пересекаются ли
прямые NK и А D ?
С
D
N
А
В
К
13
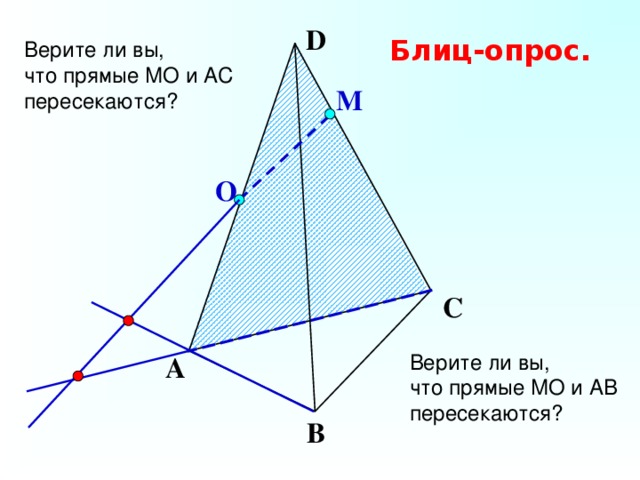
Верите ли вы,
что прямые МО и АС
пересекаются?
D
Блиц-опрос.
М
О
С
Прямые МО и АВ пересекаются, т.к. лежат в одной плоскости (А D С). Прямые МО и АВ не пересекаются, т.к. лежат в разных плоскостях (А D С) и (А D В) – эти плоскости пересекаются по прямой А D , на которой лежат все общие точки этих плоскостей.
Верите ли вы,
что прямые МО и АВ
пересекаются?
А
В
13
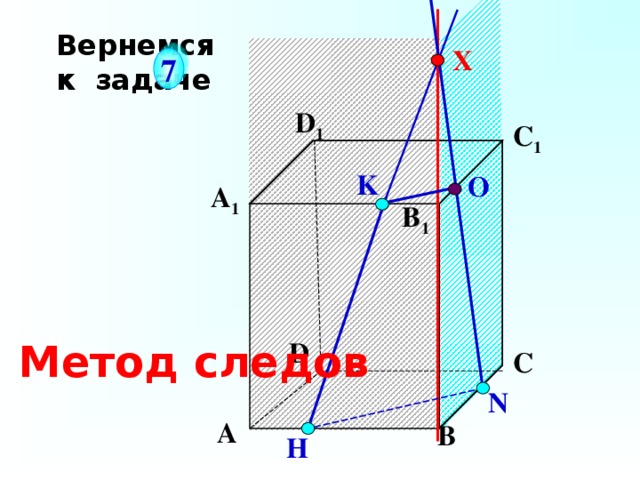
Вернемся
к задаче
X
7
D 1
С 1
K
О
А 1
B 1
Метод следов
D
С
N
А
В
H
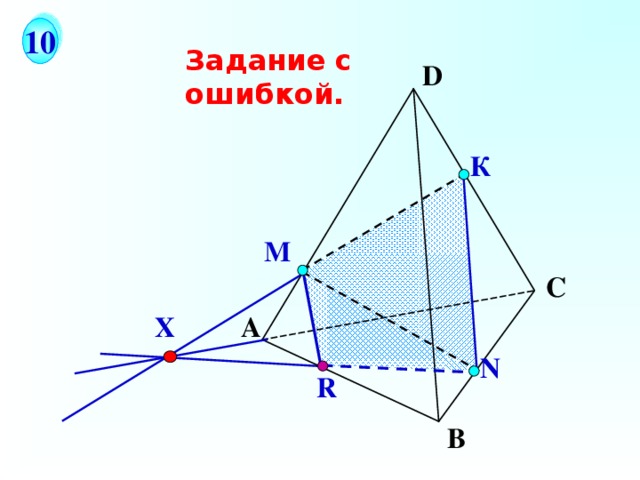
10
Задание с ошибкой.
D
К
М
С
На рисунке точки М и N не принадлежат ни одной из граней тетраэдра, поэтому отрезок находится внутри тетраэдра. Исправим чертеж методом следов.
X
А
N
R
В
17
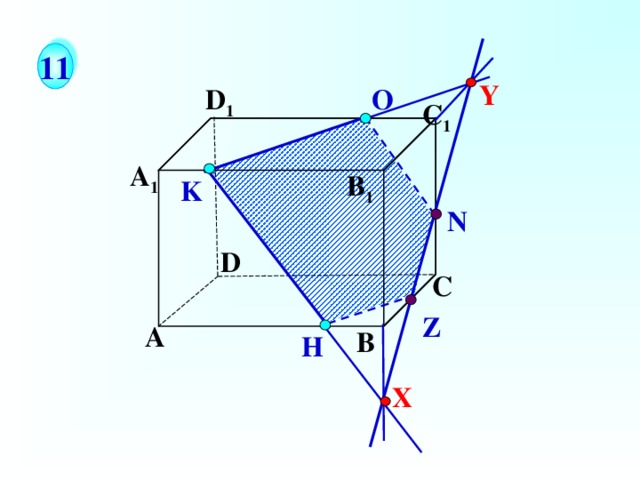
1 1
Y
D 1
О
С 1
А 1
B 1
K
N
D
С
Построить сечение параллелепипеда, проходящее через точки О, К, Н.
Z
А
В
H
X
17
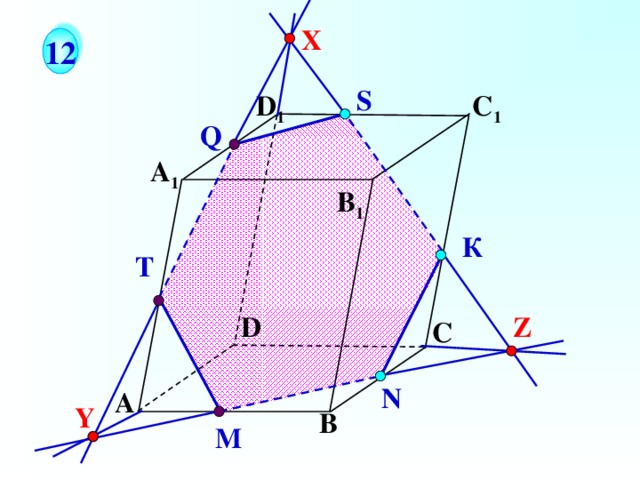
X
1 2
S
D 1
С 1
Q
А 1
B 1
К
T
Построить сечение параллелепипеда, проходящее через точки S , К, N .
D
Z
С
N
А
Y
В
M
17
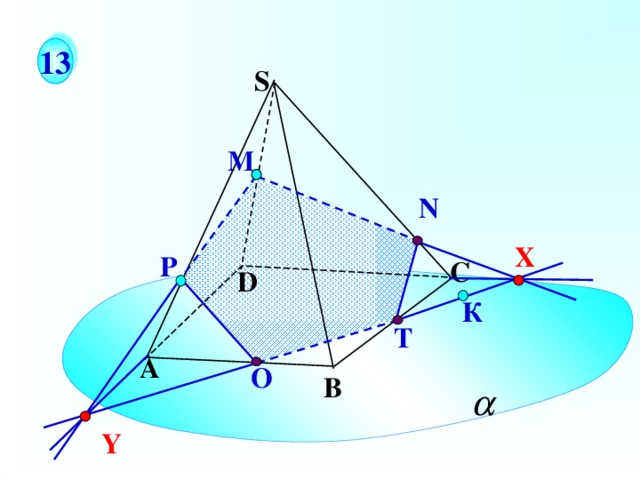
1 3
S
М
N
X
Р
С
D
К
Построить сечение многогранника плоскостью, проходящей через точки М, Р, К , если К принадлежит плоскости a .
Т
А
О
В
Y
21
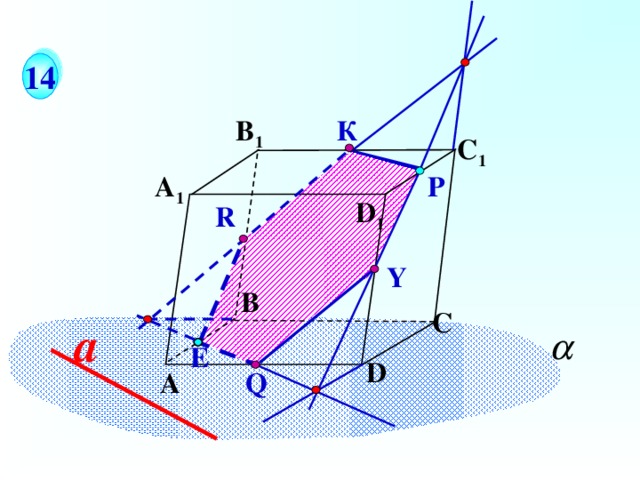
14
К
B 1
С 1
P
А 1
D 1
R
Y
B
С
Зив Б.Г. Дидактические материалы по геометрии для 10 класса. – 2-е изд. – М.: Просвещение, 1997. – 144 с.: ISBN 5-09-007468-2.
а
Е
D
А
Q
21
Отметьте внутреннюю точку M грани АА 1 В 1 В.
9
D 1
С 1
B 1
А 1
Постройте сечение параллелепипеда, проходящее через т.М параллельно:
г) плоскости В DD 1
М
Геометрия Л.С.Атанасян, 10-11. Задача № 82(в).
D
С
В
А
21
Домашняя работа
П.14;
№ 71, 72, 81, 82.
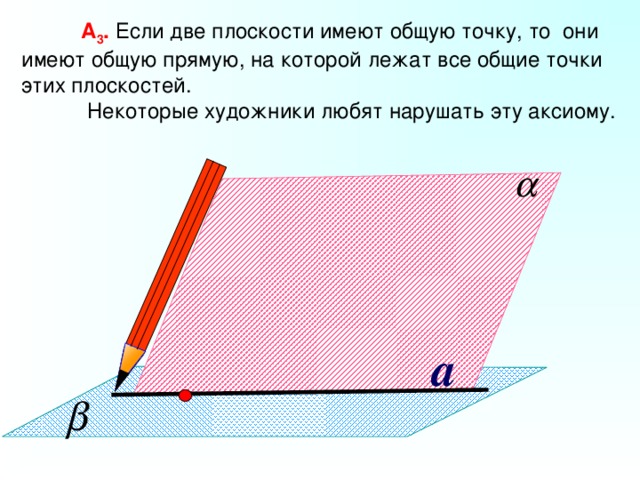
А 3 . Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.
Некоторые художники любят нарушать эту аксиому.
Геометрия: Учеб. Для 10-11 кл. общеобразова. учреждений / Л.С.Атанасян, В.Ф.Бутузов, С.Б.Кадомцев и др. – 9-е изд., с изм. – М.: Просвящение, 2000. – 206 с.:ил. – ISBN 5-09-008612-5.
а
Это интересно!
Многие художники, искажая законы перспективы, рисуют необычные картины. Кстати, эти рисунки очень популярны среди математиков. В сети Internet можно найти множество сайтов, где публикуются эти невозможные объекты.
Популярные художники Морис Эшер, Оскар Реутерсвард, Жос де Мей и другие, удивляли своими картинами математиков.
http://www.im-possible.info/english/art/mey/mey2.html
http://alone.sammit.kiev.ua/moremind/illusion/index.html
http://lib.world-mobile.net/culture/special/imp/imp-world-r.narod.ru/art/index.html
"Такое может нарисовать только тот, кто делает дизайн, не зная перспективы..."
Жос де Мей
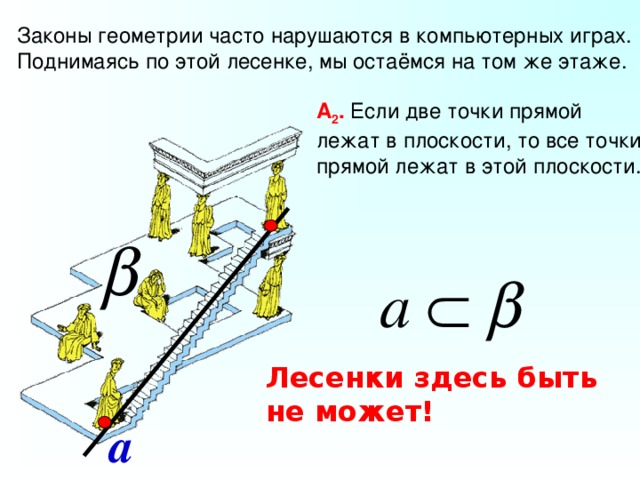
Законы геометрии часто нарушаются в компьютерных играх.
Поднимаясь по этой лесенке, мы остаёмся на том же этаже.
А 2 . Если две точки прямой
лежат в плоскости, то все точки
прямой лежат в этой плоскости.
Геометрия: Учеб. Для 10-11 кл. общеобразова. учреждений / Л.С.Атанасян, В.Ф.Бутузов, С.Б.Кадомцев и др. – 9-е изд., с изм. – М.: Просвящение, 2000. – 206 с.:ил. – ISBN 5-09-008612-5.
Лесенки здесь быть не может!
а
Получите свидетельство
Вход
Презентация по математике на тему "Построение сечений многогранников" (1.29 MB)
0
1385
424
Нравится
0
