1.Тип урока: комбинированный; содержит следующие учебно-воспитательные дидактические моменты: организационный момент (5 мин), устная работа (5 мин), закрепление темы (10 мин), этап проверки усвоения знаний в виде игры-эстафеты (15 мин), сообщение доклада (3 мин), итог урока ( 2 мин).
2.Форма урока: традиционная
3.Цели урока:
систематизировать и обобщить знания о свойствах функции, развивать навыки построения и чтения графиков функций, умение работать с тестовыми заданиями;
развивать логическое мышление, умение делать обобщения и выводы;
воспитывать сознательное отношение к учебе, познавательную активность, интерес к предмету и его истории.
4.Задачи:
Обучающая; составить план исследования функции
Развивающая; формировать ключевые компетентности учащихся: развивать учебно-интеллектуальные умения, (анализировать, сравнивать, обобщать, выделять главное); учебно-познавательные умения (развивать навыки построения и чтения графиков функций, аргументированно доказывать, умение математическим языком выражать свои мысли, делать обобщения и выводы); поисково-информационные умения; учебно-организационные умения (умение осуществлять самоконтроль и самоанализ учебной деятельности, сотрудничать при решении поставленных задач).
Воспитывающая; воспитывать культуру работы с чертежами, ответственность, трудолюбие, добросовестность, умение работать в коллективе, развивать интерес к предмету
5.Методы обучения:
Методы организации и осуществления учебно-познавательной деятельности; практические методы – (выполнение заданий теста), репродуктивные (воспроизведение), индуктивные (от частного к общему), конкретные и абстрактные методы – синтез и анализ; сравнение, обобщение, методы учебной работы под руководством учителя; методы самостоятельной учебной деятельности ученика.
Методы стимулирования и мотивации учебной деятельности;
эмоциональные - поощрение, порицание, волевые - предъявление учебных требований, информирование о обязательных результатах обучения, формирование ответственного отношения к учению, познавательные затруднения
Методы контроля и самоконтроля учебной деятельности.
а) устные, письменные;
б) фронтальные, групповые, индивидуальные;
в) итоговые, текущие;
6.Оборудование:
портрет французского математика Рене Декарта
карточки с заданиями для игры
тестовый материал
7.Актуальность:
задания по данной теме встречаются в тестах единого государственного экзамена по математике в 9 классе (в новой форме) и 11 классе;
чтение графиков функций имеет большое практическое значение.
8.Конечный результат: ученики должны правильно находить область определения функции, нули функции, промежутки возрастания и убывания функции, область значений функции.
9.Оформление доски:
Тема урока: «Свойства функции».
Таблица для работы с тестом.
График исследуемой функции.
Записано домашнее задание.
Ход урока
1. Организационный момент; (приветствие учащихся, работа с журналом, сообщение темы и плана урока)
Здравствуйте, дорогие ребята! Проверьте готовность к уроку: нам сегодня потребуются чертежные инструменты для построения графика. Настройтесь на совместную работу на уроке при закреплении темы: «Свойства функции». Будьте внимательны, требовательны и в то же время доброжелательны друг к другу.
2. Проверка домашнего задания;( собрать тетради)
Ученики передают тетради с домашним заданием на первые парты. Учитель начинает устный опрос определений по данной теме.
Фронтальный опрос:
- Что называется областью определения функции?
- Что называется областью значения функции?
- Дайте определение функции, убывающей на промежутке?
- Дайте определение функции, возрастающей на промежутке?
- Какую функцию называют ограниченной сверху?
- Какую функцию называют ограниченной снизу?
- Какие точки называются нулями функции?
3. Этап подготовки к активной учебно-познавательной деятельности.
Ребята! Запишите дату и тему урока: «Свойства функции». Предлагаю вместе четко и однозначно сформулировать образовательную цель нашего урока, определить его задачи. Обратите особое внимание на актуальность знаний и умений по данной теме, на то, где мы можем применить знания о исследовании функции.
Совместно с учащимися формулируем триединую цель урока, направленную на его конечный результат.
4. Этап всесторонней проверки знаний.
Данный этап проводится с использованием тестовых заданий рассчитанных по количеству учеников в классе. Учащиеся решают тест и полученным ответам сопоставляют буквы по таблице, заранее приготовленной на доске, в результате правильного выполнения задания, ребята угадают фамилию известного математика. Учитель проводит четкий и доступный инструктаж выполнения данного задания.
Тест « Свойства функций» - смотрите документ
5.Этап усвоения новых знаний:
А сейчас приступаем к самому ответственному этапу урока – усвоению новых знаний. Систематизируем наши знания и запишем план исследования функции.
Область определения функции;
Область значений функции;
Нули функции;
Промежутки возрастания (убывания) функции;
Наименьшее и наибольшее значение функции;
Ограниченность сверху, снизу, ограниченность функции.
Заметим, что составленный нами план в дальнейшем будет меняться по мере изучения свойств функций. Далее предлагается по данному плану исследовать функцию.
Учащиеся самостоятельно выполняют график у себя в тетради. Учитель заранее выполняет построение графика на обратной стороне доски. Учащиеся сверяют свой график с графиком, построенным на доске, и вместе с учителем исследуют его свойства.- смотрите документ.
6. Этап закрепления новых знаний
Учитель проводит инструктаж предстоящей игры - этафеты. Учащиеся сидят на своих местах. Карточки с заданием подготовлены заранее. Они выдаются учащимся, сидящим за последними партами. В карточке 5-6 заданий, место для краткого решения и подписи учеников. Учащийся решает любое задание, ставит свою фамилию напротив решенного номера и передает лист впереди сидящему. Следующий ученик приступает к решению следующего задания. Игра заканчивается, когда все задания решены. Победившую группу (некоторых учащихся) можно оценить по бланкам ответов. Рецензирование учителя с указанием положительного и недостатков в решении заданий, конкретность предложений по ликвидации пробелов в знаниях учащихся. – смотрите документ.
Ребята, вы продуктивно поработали, теперь послушаем сообщение о жизни и деятельности французского математика Рене Декарта, чью фамилию мы сегодня уже упоминали. Докладчик выходит к доске и зачитывает своё сообщение, сопровождая свой рассказ портретом. – смотрите документ.
7. Этап подведения итогов урока.
Фронтальная беседа:
Ребята, какую новую информацию вы получили на сегодняшнем уроке? (план исследования функции, биографию Рене Декарта)
Используя наш план, проведите устное исследование линейной функции с положительным коэффициентом? (Область определения и область значения – вся числовая прямая, функция постоянно возрастает, функция неограниченна)
В чем заключаются заслуги Рене Декарта? (ввёл обозначение переменных, степеней и коэффициентов, создал современную систему координат)
Характеристика работы класса по плану:
Анализ успешности овладения знаниями и способами деятельности.
Показать типичные недостатки в знаниях, умениях и навыках, показать пути их преодоления.
Показать успешность овладения содержанием урока.
Определение мер для последующей работы тем, кто затрудняется.
Определение эффективности урока и на этом основании составление плана пути ее повышения.
Комментирование оценок.
8. Домашнее задание.
Информация о домашнем задании.
Для дальнейшего развития знаний и подготовки к успешному обучению необходимо выполнить дома следующую работу. Фронтальное задание:
Повторить все определения по теме «Свойства функции» Глава 3, §9;
- Решить задачи: № 105, № 110 (а,в) с применением плана исследования функции и построением графика (даются методические советы по выполнению домашнего задания); на повторение № 128 (г)

 Получите свидетельство
Получите свидетельство Вход
Вход


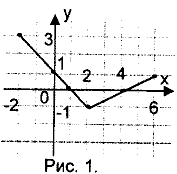 . Найдите область определения функции, изображенной на рис.1.
. Найдите область определения функции, изображенной на рис.1.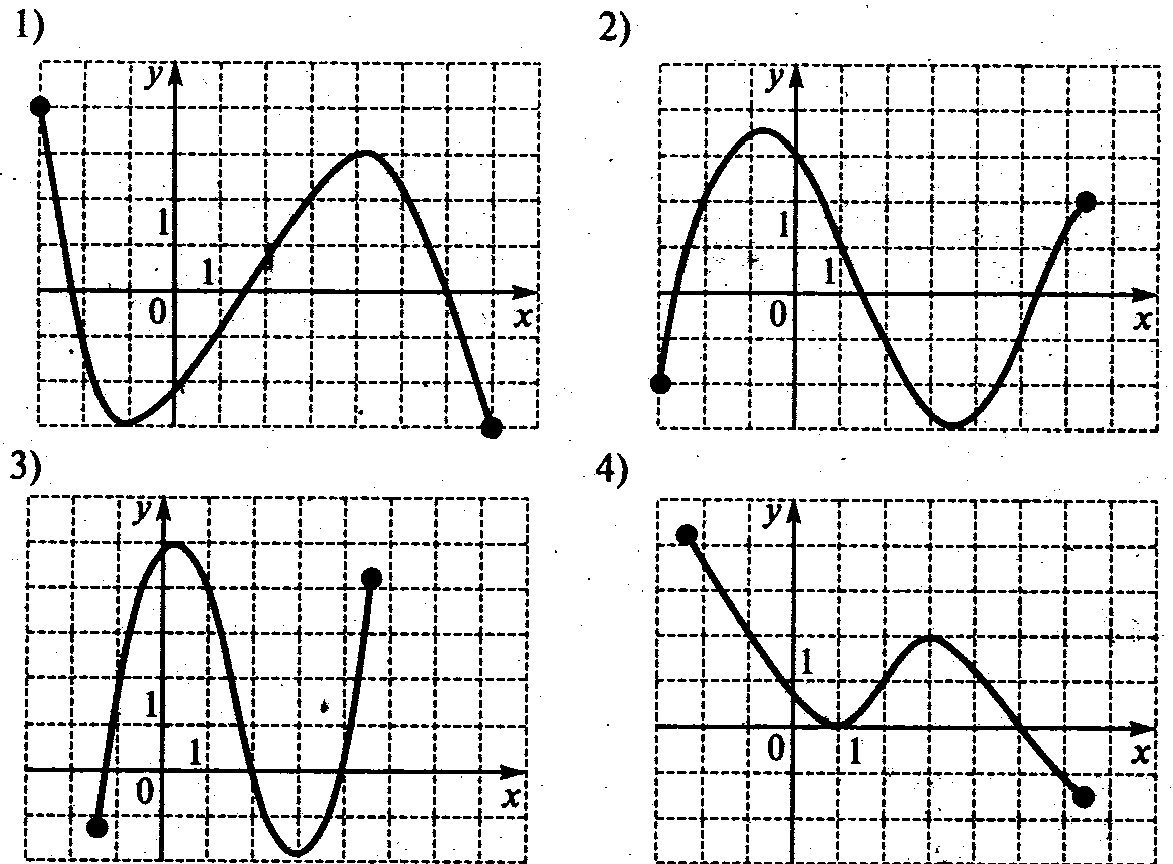
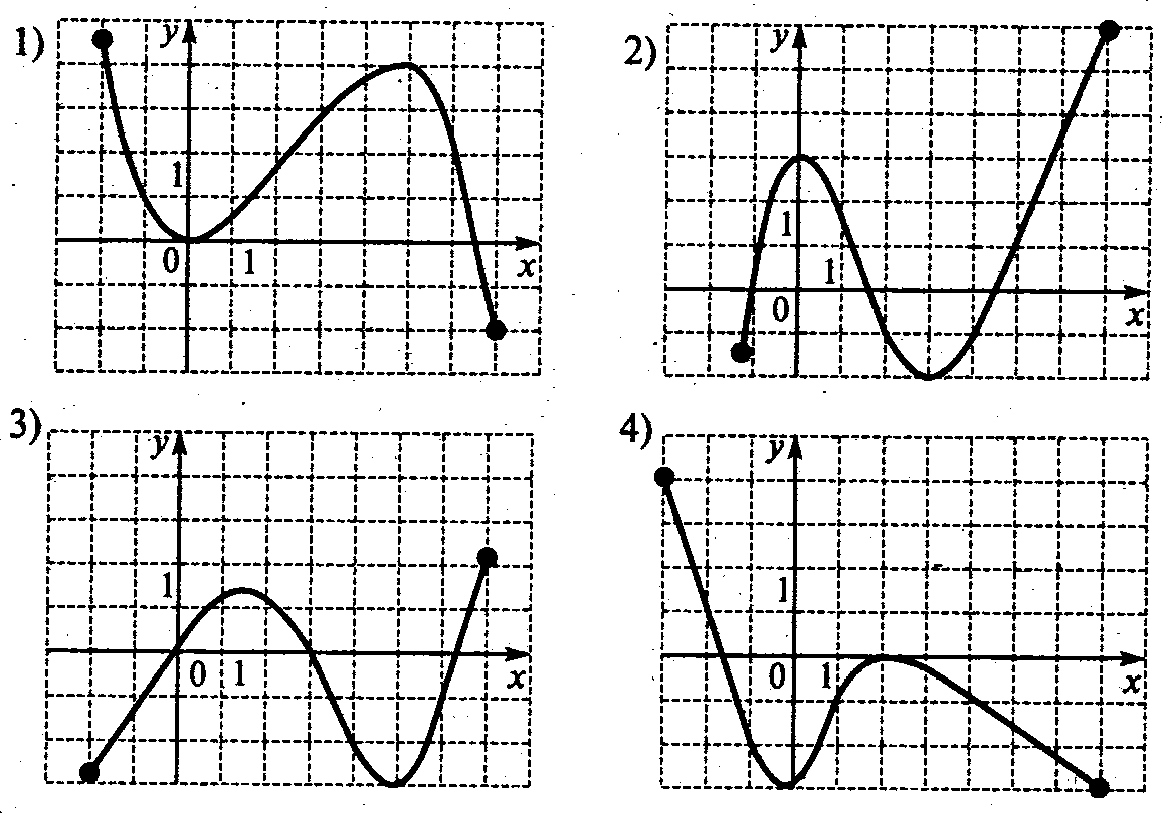
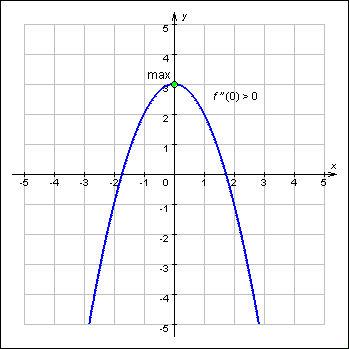
 . На рисунке изображен график функции у = f(x). Из приведенных утверждений выберите верное.
. На рисунке изображен график функции у = f(x). Из приведенных утверждений выберите верное.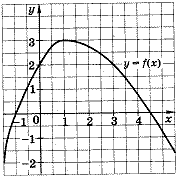
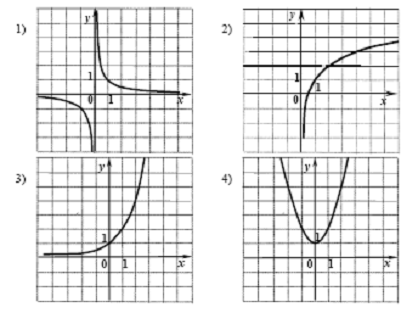
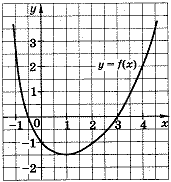
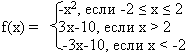 остройте график функции у = ƒ(x), где
остройте график функции у = ƒ(x), где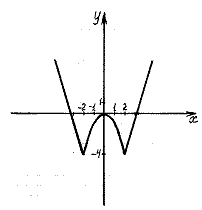









 Свойства функций (0.35 MB)
Свойства функций (0.35 MB)
 0
0 1755
1755 275
275 Нравится
0
Нравится
0



