Свойства функции

Презентация состоит из 35 слайдов.

Функция называется возрастающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует большее значение функции.

Иными словами,  функцию y = f(x) называют возрастающей в некотором промежутке, если для любых x₁ и x₂ из этого промежутка, таких, что x₂ > x₁, выполняется неравенство  f(x₂) > f(x₁).

Функция называется убывающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует меньшее значение функции.

Иными словами,  функцию y = f(x) называют возрастающей в некотором промежутке, если для любых x₁ и x₂ из этого промежутка, таких, что x₂ < x₁, выполняется неравенство  f(x₂) < f(x₁).

Свойства линейной функции

y = kx + b, где k не равно 0

1) Найдём нули функции.

2) Выясним при каких значениях x f(x) >0.

3) Выясним при каких значениях x f(x) < 0.

4) Докажем, что при k > 0 функция возрастающая, при k < 0 функция убывающая.

Свойства функции.

Урок №2

Сентябрь

2004 г

Учитель

Козина Н.А.

Карточка №1

• № 1. Известно, что f(x) = 8 -3x 2 .
• Найдите f(-3).
• № 2. Найдите значение x, при котором функция, заданная формулой f(x) = 0,3x – 5, принимает значение равное -8.
• № 3. Найдите область определения функции, заданной формулой

• № 4. По рисунку №4(в) укажите область значений функции.

Карточка №2

• № 1. Известно, что f(x) = 7 -2x 2 .
• Найдите f(-3).
• № 2. Найдите значение x, при котором функция, заданная формулой f(x) = 0,8x – 5, принимает значение равное -9.
• № 3. Найдите область определения функции, заданной формулой

• № 4. По рисунку №4(а) укажите область значений функции.

Функция задана формулой

Найдите значение функции при

4

а)

2,75

б)

-4

в)

Найдите область определения функции:

x - любое

а)

x ≥ 0

б)

x ≠ 3

в)

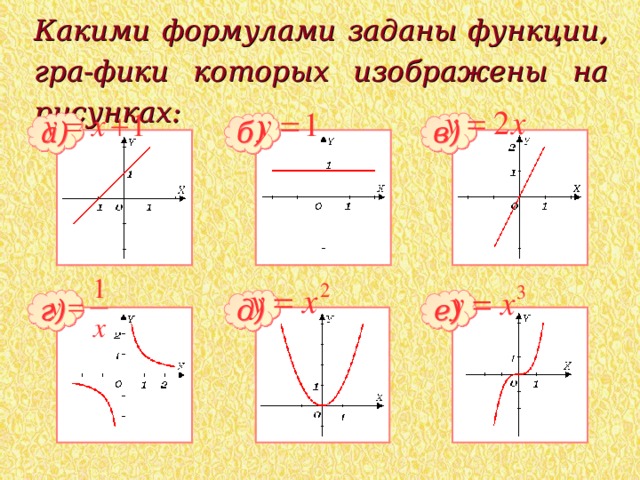
Какими формулами заданы функции, гра-фики которых изображены на рисунках:

а)

в)

б)

г)

д)

е)

Устно.

• Найдите область определения функции.
• Множество всех чисел.
• Область значений функции.
• (-  ;4 ].

0; При x  (-3;1) . " width="640"

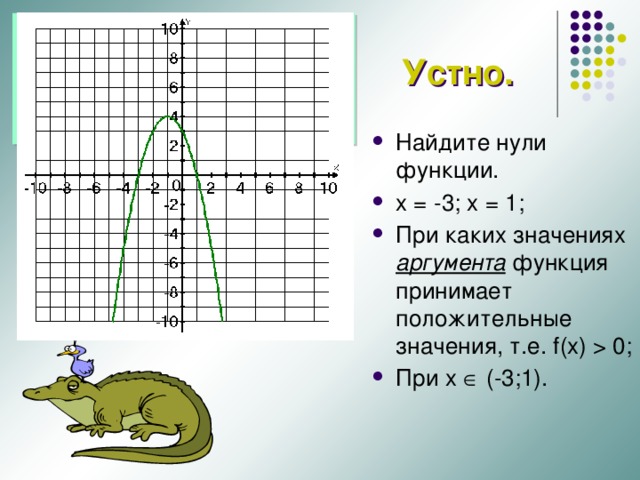
Значения аргумента, при которых функция обращается в нуль, называют нулями функции.

Устно.

• Найдите нули функции.
• x = -3; x = 1;
• При каких значениях аргумента функция принимает положительные значения, т.е. f(x) 0;
• При x  (-3;1) .

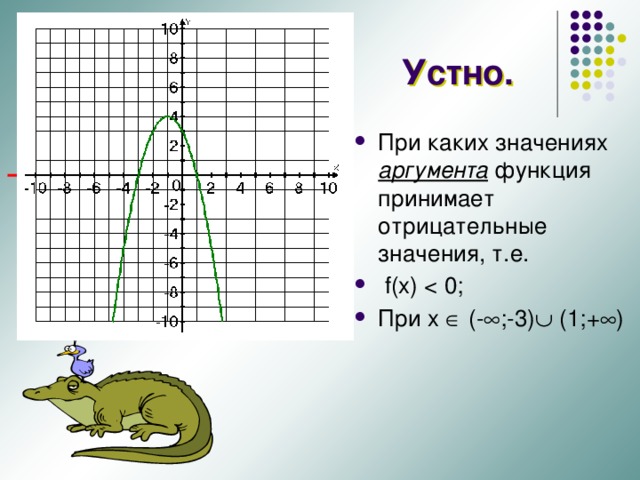
Устно.

• При каких значениях аргумента функция принимает отрицательные значения, т.е.
• f(x)
• При x  (-  ;-3)  (1;+  )

Устно.

• При каких значениях аргумента функция возрастает?
• При x  (-  ;-1 ]
• При каких значениях аргумента функция убывает?
• При x  [-1;+  )

Свойства функций

Определение.

• Функция называется возрастающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует большее значение функции.

x 1 , выполняется неравенство f(x 2 ) f(x 1 ). " width="640"

Свойства функций

Определение.

• Иными словами,
• функцию y = f(x) называют возрастающей в некотором промежутке,
• если для любых x 1 и x 2 из этого промежутка, таких, что x 2 x 1 , выполняется неравенство
• f(x 2 ) f(x 1 ).

x 1 , то f(x 2 ) f(x 1 ). f(x 1 ) x 2 x 1 " width="640"

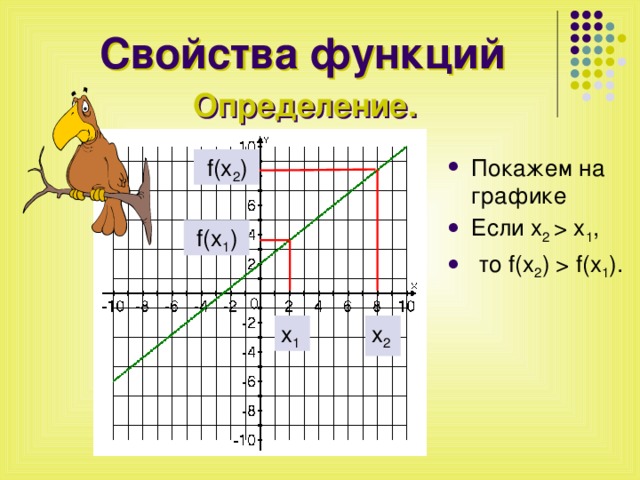
Свойства функций

Определение.

f(x 2 )

• Покажем на графике
• Если x 2 x 1 ,
• то f(x 2 ) f(x 1 ).

f(x 1 )

x 2

x 1

Свойства функций

Определение.

• Функция называется убывающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует меньшее значение функции.

x 1 , выполняется неравенство f(x 2 ) " width="640"

Свойства функций

Определение.

• Иными словами,
• функцию y = f(x) называют убывающей в некотором промежутке,
• если для любых x 1 и x 2 из этого промежутка, таких, что x 2 x 1 , выполняется неравенство
• f(x 2 )

x 1 , то f(x 2 ) f(x 1 ) x 2 x 1 f(x 2 ) " width="640"

Свойства функций

Определение.

• Покажем на графике
• Если x 2 x 1 ,
• то f(x 2 )

f(x 1 )

x 2

x 1

f(x 2 )

Свойства линейной функции

y = kx + b, где k  0

• 1) Найдём нули функции.
• kx + b = 0;
• kx = -b;

0. kx + b 0; kx -b; Рассмотрим 2 случая: k 0 и k k 0 " width="640"

Свойства линейной функции

y = kx + b, где k  0

2) Выясним при каких значениях x f(x) 0.

kx + b 0;

kx -b;

Рассмотрим 2 случая: k 0 и k

• k 0

0. kx + b 0; kx -b; Рассмотрим 2 случая: k 0 и k k " width="640"

Свойства линейной функции

y = kx + b, где k  0

2) Выясним при каких значениях x f(x) 0.

kx + b 0;

kx -b;

Рассмотрим 2 случая: k 0 и k

• k

0 и k k 0 " width="640"

Свойства линейной функции

y = kx + b, где k  0

3) Выясним при каких значениях x f(x)

kx + b

kx

Рассмотрим 2 случая: k 0 и k

• k 0

0 и k k " width="640"

Свойства линейной функции

y = kx + b, где k  0

3) Выясним при каких значениях x f(x)

kx + b

kx

Рассмотрим 2 случая: k 0 и k

• k

0 функция возрастающая, при k Рассмотрим 2 случая: k 0 и k k 0; Пусть x 2 x 1 , т.е. x 2 –x 1 0. Найдем f(x 2 ) –f(x 1 ) = kx 2 +b –kx 1 – b = k(x 2 – x 1 ). Но k 0 и x 2 – x 1 0, значит, f(x 2 ) – f(x 1 ) 0. Т.о. функция – возрастающая. " width="640"

Свойства линейной функции

y = kx + b, где k  0

4)Докажем, что при k 0 функция возрастающая, при k

Рассмотрим 2 случая: k 0 и k

• k 0;
• Пусть x 2 x 1 , т.е. x 2 –x 1 0.
• Найдем f(x 2 ) –f(x 1 ) = kx 2 +b –kx 1 – b = k(x 2 – x 1 ).
• Но k 0 и x 2 – x 1 0, значит, f(x 2 ) – f(x 1 ) 0.
• Т.о. функция – возрастающая.

0 функция возрастающая, при k Рассмотрим 2 случая: k 0 и k k Пусть x 2 x 1 , т.е. x 2 –x 1 0. Найдем f(x 2 ) –f(x 1 ) = kx 2 +b –kx 1 – b = k(x 2 – x 1 ). Но k 0, значит, f(x 2 ) – f(x 1 ) Т.о. функция –убывающая. " width="640"

Свойства линейной функции

y = kx + b, где k  0

4)Докажем, что при k 0 функция возрастающая, при k

Рассмотрим 2 случая: k 0 и k

• k
• Пусть x 2 x 1 , т.е. x 2 –x 1 0.
• Найдем f(x 2 ) –f(x 1 ) = kx 2 +b –kx 1 – b = k(x 2 – x 1 ).
• Но k 0, значит, f(x 2 ) – f(x 1 )
• Т.о. функция –убывающая.

СВОЙСТВА ФУНКЦИЙ

Урок №3

0, если x  [-7;-5)  (-3;1)  (4;5] f(x) " width="640"

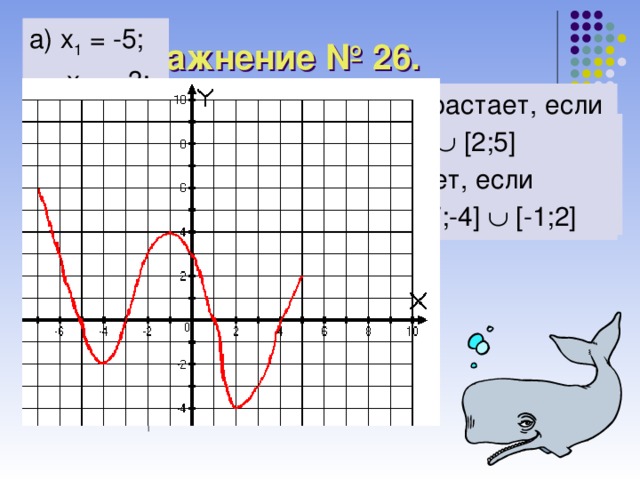
а) x 1 = -5;

x 2 = -3;

x 3 = 1;

x 4 = 4.

Упражнение № 26.

б) f(x) возрастает, если

x  [-4;-1]  [2;5]

f(x) убывает, если

x  [-7;-4]  [-1;2]

б) f(x) 0, если

x  [-7;-5)  (-3;1)  (4;5]

f(x)

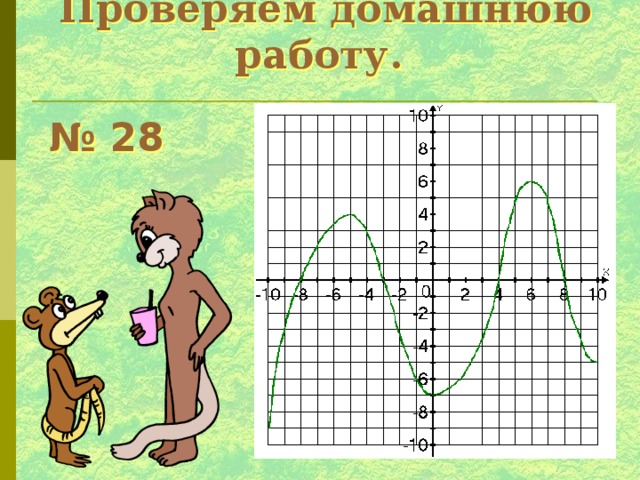
Проверяем домашнюю работу.

№ 28

Найдите значение функции, заданной формулой, соответствующее значению аргумента, равному:

Найдите значение функции, заданной формулой, соответствующее значению аргумента, равному:

а)

0

0

б)

-3

-36

в)

4,5

1,5

Найдите область определения функции, заданной формулой:

Найдите область определения функции, заданной формулой:

а)

в)

x - любое

x - любое

г)

б)

x ≥ 6

x ≠ -5

Решите неполные квадратные уравнения:

Решите неполные квадратные уравнения:

а)

Ответ: x 1 =0; x 2 =5.

Решите неполные квадратные уравнения:

Решите неполные квадратные уравнения:

б)

в)

Ответ: x 1 =3;

x 2 =-3.

Ответ: x 1 =0; x 2 =-4.

Решите неполные квадратные уравнения:

Решите неполные квадратные уравнения:

г)

Ответ: нет корней.

д)

Ответ:

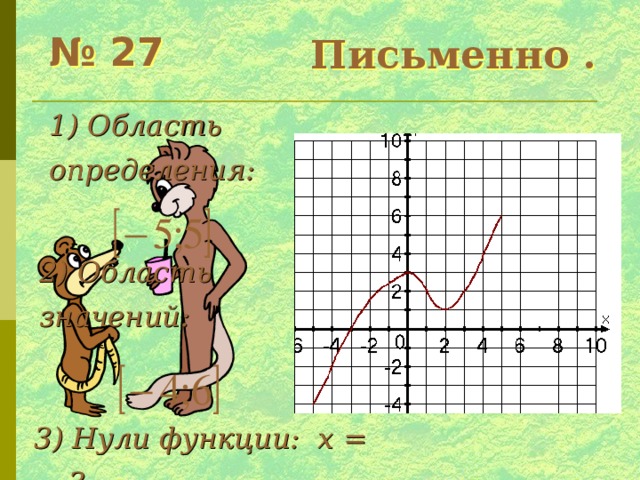
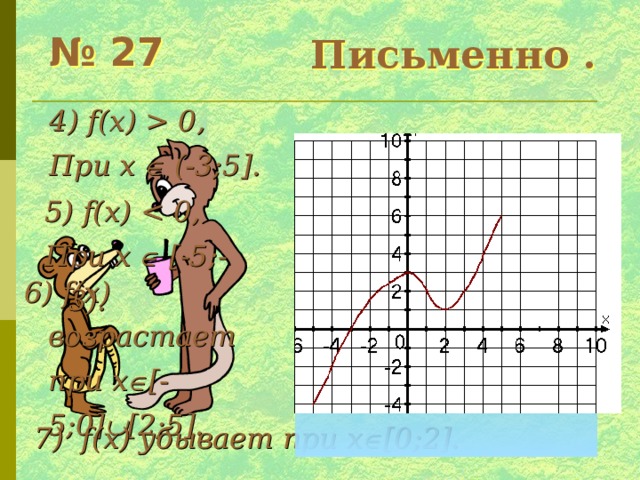
Письменно .

№ 27

• Область

определения:

2) Область

значений:

3) Нули функции: x = -3.

0, При x  (-3;5]. 5) f(x) При x  [-5;-3). 6) f(x) возрастает при x  [-5;0]  [2;5]. 7) f(x) убывает при x  [0;2]. " width="640"

Письменно .

№ 27

4) f(x) 0,

При x  (-3;5].

5) f(x)

При x  [-5;-3).

6) f(x) возрастает при x  [-5;0]  [2;5].

7) f(x) убывает при x  [0;2].

Решите уравнения:

Решите уравнения:

а)

б)

в)

г)

д)

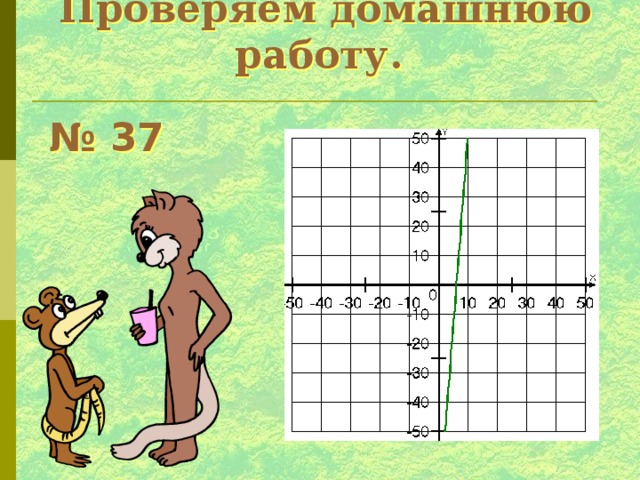
Проверяем домашнюю работу.

№ 37