Свойства биссектрисы угла

Этапы урока:

- организационный;

- этап проверки домашнего;

- задания;

- актуализация знаний учащихся;

- объяснение нового материала;

- закрепление;

- проверка усвоения.

Цели урока:

- Доказать, свойство биссектрисы угла (теорема);

- Доказать следствие;

- Уметь применить теорему и следствие при решении задач.

Повторение (устный опрос)

- Определение биссектрисы угла;

- Признаки равенства треугольников;

- Признаки равенства прямоугольных треугольников;

- Расстояние от точки до прямой.

Свойства биссектрисы угла

Урок геометрии в 8 классе

Учитель математики Цоколова Т.А .

Тип урока: урок усвоения новых знаний Этапы урока: - организационный - этап проверки домашнего задания - актуализация знаний учащихся - объяснение нового материала; - закрепление - проверка усвоения

Цели у рока

• Доказать, свойство

биссектрисы угла ( теорема )

• Доказать следствие
• Уметь применить теорему и следствие при решении задач

Повторение (устный опрос)

• Определение биссектрисы угла
• Признаки равенства треугольников
• Признаки равенства прямоугольных треугольников
• Расстояние от точки до прямой

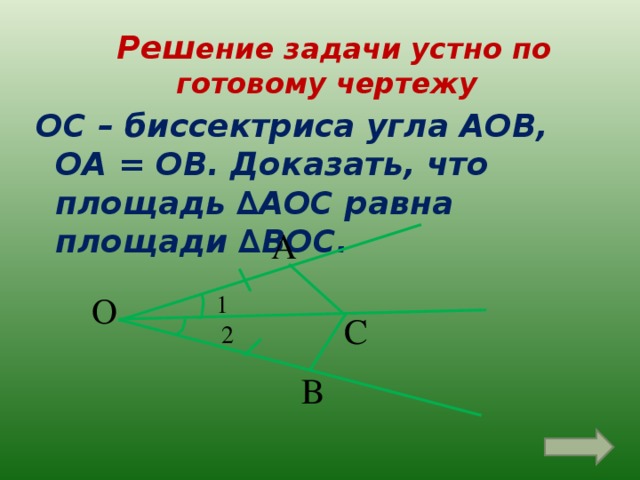
Реш ение задачи устно по готовому чертежу

ОС – биссектриса угла АОВ, ОА = ОВ. Доказать, что площадь ∆АОС равна площади ∆ВОС.

А

1

О

С

2

В

Теорема

Каждая точка биссектрисы неразвёрнутого угла равноудалена от его сторон .

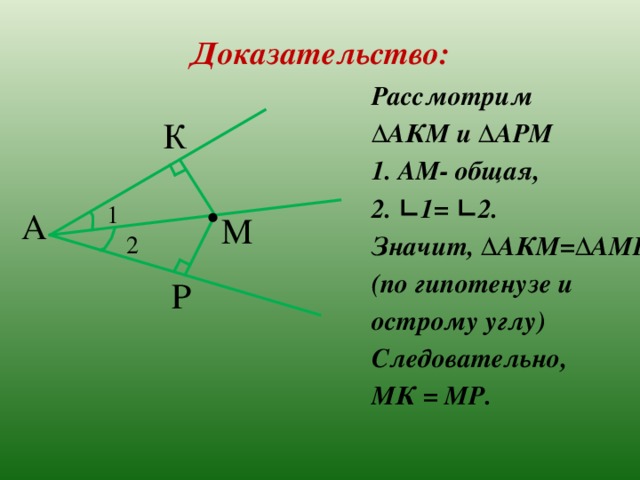
Доказательство:

Рассмотрим

∆ АКМ и ∆АРМ

1. АМ- общая,

2. ∟1= ∟2.

Значит, ∆АКМ=∆АМР

(по гипотенузе и

острому углу)

Следовательно,

МК = МР.

К

.

1

А

М

2

Р

Теорема (обратная)

Каждая точка, лежащая внутри угла и равноудалённая от сторон угла, лежит на его биссектрисе.

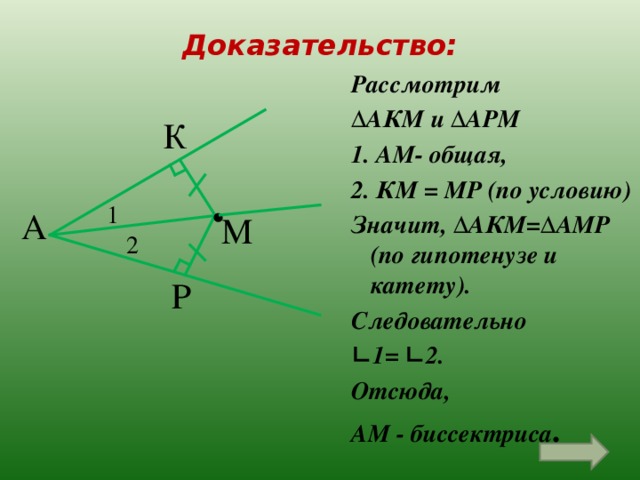
Доказательство:

Рассмотрим

∆ АКМ и ∆АРМ

1. АМ- общая,

2. КМ = МР (по условию)

Значит, ∆АКМ=∆АМР (по гипотенузе и катету).

Следовательно

∟ 1= ∟2.

Отсюда,

АМ - биссектриса .

К

.

1

А

М

2

Р

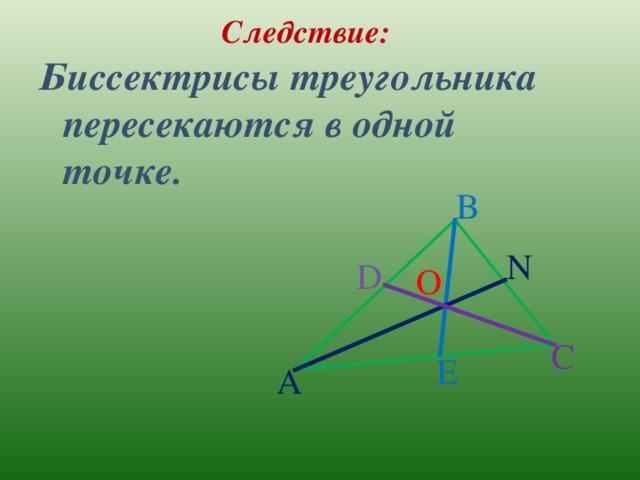
Следствие:

Биссектрисы треугольника пересекаются в одной точке.

B

N

D

O

C

E

A

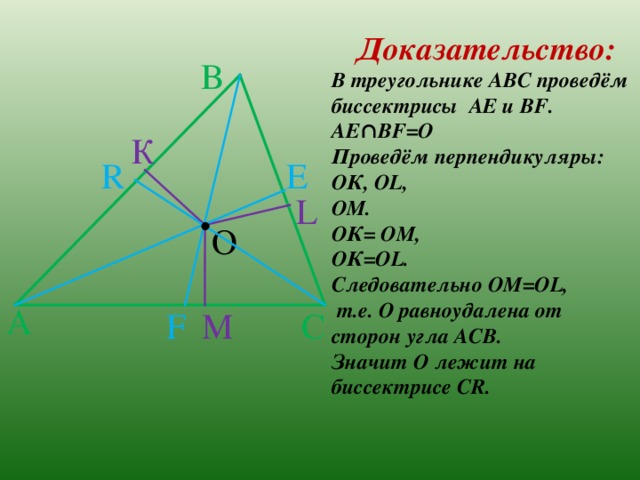
Доказательство:

В треугольнике АВС проведём биссектрисы АЕ и В F .

АЕ∩В F =О

Проведём перпендикуляры:

ОК, О L ,

ОМ.

ОК= ОМ,

ОК=О L .

Следовательно ОМ=О L ,

т.е. О равноудалена от

сторон угла АСВ.

Значит О лежит на

биссектрисе С R .

В

К

Е

R

.

.

L

О

А

С

М

F

Выучить:

Каждая точка биссектрисы

неразвёрнутого угла равноудалена от его сторон

Каждая точка, лежащая внутри угла и равноудалённая от сторон угла, лежит на его биссектрисе

Биссектрисы треугольника

пересекаются в одной точке

Закрепление (номера из учебника)

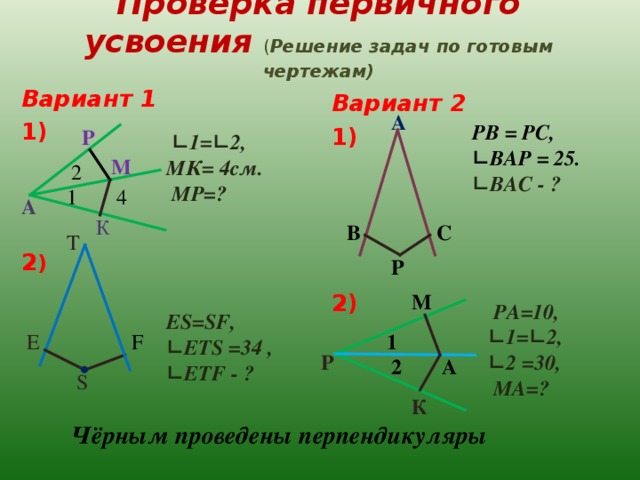
Проверка первичного усвоения ( Решение задач по готовым чертежам)

Вариант 1

1)

2 )

Вариант 2

1)

2)

А

РВ = РС,

∟ ВАР = 25.

∟ ВАС - ?

РА=10,

∟ 1=∟2 ,

∟ 2 =30,

МА=?

P

∟ 1=∟2 , МК= 4см.

МР=?

ES=SF ,

∟ ETS = 3 4 ,

∟ ETF - ?

M

2

1

4

А

К

В

С

Т

Р

М

.

E

F

1

Р

А

2

S

К

Чёрным проведены перпендикуляры

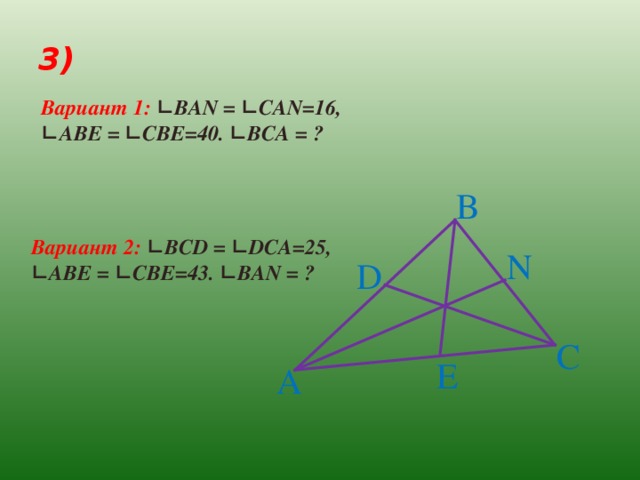
3)

Вариант 1: ∟ВА N = ∟ CAN= 16 ,

∟ A В E = ∟ CBE=40. ∟В C А = ?

B

Вариант 2: ∟В CD = ∟ DCA= 25 ,

∟ A В E = ∟ CBE=4 3 . ∟ВА N = ?

N

D

C

E

A

Ответы (взаимопроверка)

Вариант2.

• 1) 50
• 2) 5
• 3) 34

Вариант1.

• 1) 4
• 2) 68
• 3) 22

Домашнее задание: