Свойство функции (четность)

Свойство функции (четность)

Юрьева Е.С.

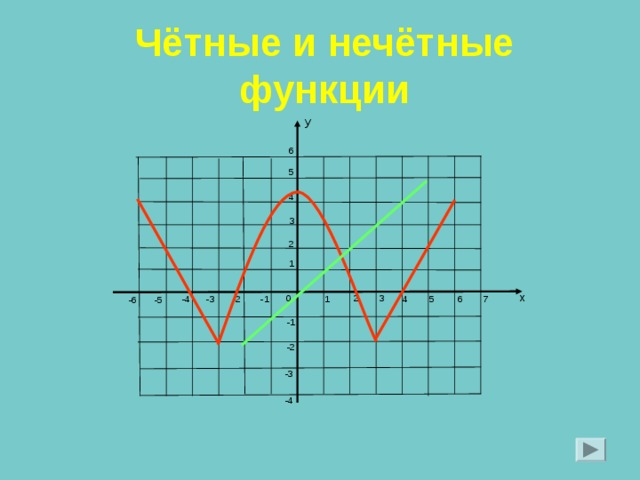
Чётные и нечётные функции

у

6

5

4

3

2

1

х

о

2

3

1

-4

-3

-2

-1

7

5

4

6

-6

-5

-1

-2

-3

-4

Определение

Функция y=f (x) называется чётной, если:

• D (f) симметрична относительно нуля;

2) для любого х Є D (f) верно равенство: f (-x) = f (x).

Функция y=f (x) называется нечётной, если:

1) D (f) симметрична относительно нуля;

2) для любого х Є D (f) верно равенство: f (-x) = - f (x).

Выяснить является ли функция чётной или нечётной:

у(х) = 7x +x³

Решение: D (y) = R

y ( - x ) =

= 7( - x ) +( - x )³=

= - 7 x - x³ =

= - (7x +x³ )

= - y (x)

Значит, функция - нечётная

y (х) = 5 x²- |X|

Решение: D (y) = R

y ( - x ) =

=5 ( - x )² - | - x | =

= 5 x ² - | x |=

= y (x)

Значит, функция - чётная

Функция f (x) – чётная,

f ( 3 ) = 25 , тогда f ( -3 ) = ?

f ( -8 ) = -71, тогда f ( 8 ) = ?

25

-71

Функция g ( x ) – нечётная,

g ( 7 ) = 43, тогда g ( -7 ) = ?

g ( - 2 ) = -64, тогда g ( 2 ) = ?

- 43

64

Существуют функции, которые не обладают

свойствами чётности или нечётности.

у (х) = х 2 + 5х

D (y) = R

у ( - х ) = ( - х) 2 +5 (- х) = х 2 – 5 х

у ( - х ) у (х )

у ( - х ) - у (х )

Значит, данная функция не является ни чётной, ни нечётной.

• Является ли функция четной или нечетной?

чётная

нечётная

нечётная

чётная

ни чётная, ни нечётная

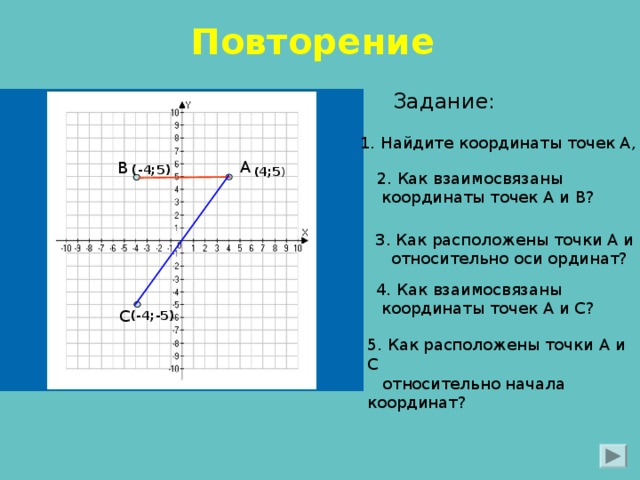
Повторение

Задание:

1. Найдите координаты точек А, В, С

A

B

(-4;5)

( 4;5 )

2. Как взаимосвязаны

координаты точек А и В?

3. Как расположены точки А и В

относительно оси ординат?

4. Как взаимосвязаны

координаты точек А и С?

C

(-4;-5)

5. Как расположены точки А и С

относительно начала координат?

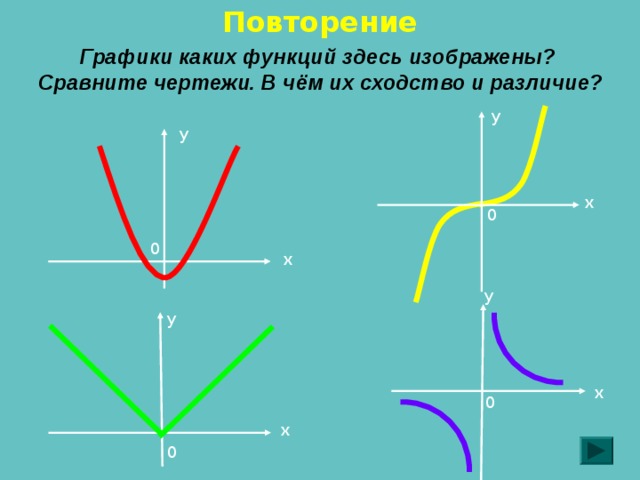
Повторение

Графики каких функций здесь изображены? Сравните чертежи. В чём их сходство и различие?

у

у

х

0

0

х

у

у

х

0

х

0

Свойство графиков

чётных функций

По определению:

если функция – чётная, то противоположным значениям х

соответствуют равные значения у.

Сделайте вывод: 1) об области определения функции;

2) о расположении точек графика чётной функции.

Вывод: 1) область определения симметрична относительно точки (0; 0);

2) график чётной функции состоит из точек, симметричных

относительно оси ординат.

График чётной функции симметричен

относительно оси ординат.

Свойство графиков

нечётных функций

По определению:

если функция – нечётная, то противоположным значениям х

соответствуют противоположные значения у.

Сделайте вывод: 1) об области определения функции;

2) о расположении точек графика нечётной функции.

Вывод:1) область определения симметрична относительно точки (0; 0);

2) график нечётной функции состоит из точек, симметричных

относительно начала координат.

График нечётной функции симметричен

относительно начала координат.

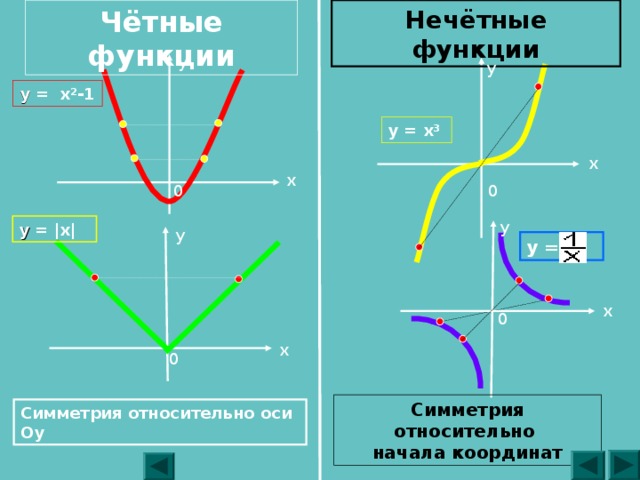
Нечётные функции

Чётные функции

у

у

y = x² -1

y = x³

х

х

0

0

у

y = | x |

у

y =

х

0

х

0

Симметрия относительно

начала координат

Симметрия относительно оси Оy

• Может ли быть четной или нечетной функция,
• областью определения которой является:

а) промежуток [ -2; 5 ]

нет

да

б ) промежуток ( -5; 5 )

в) промежуток ( -3; 3 ]

нет

г) объединение промежутков

[ -10; -2] и [ 2; 10 ]

да

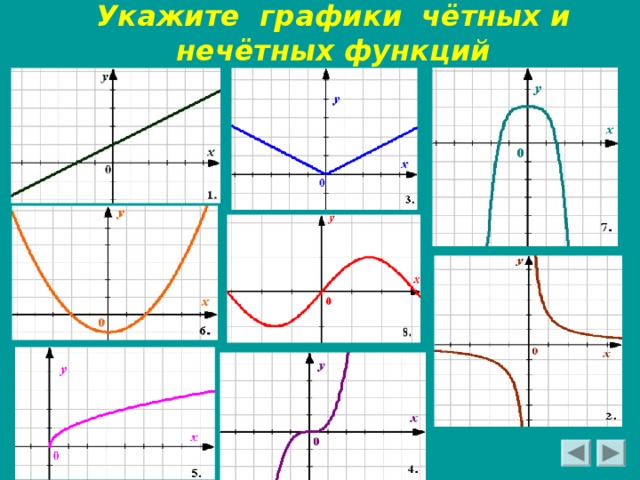
Укажите графики чётных и нечётных функций

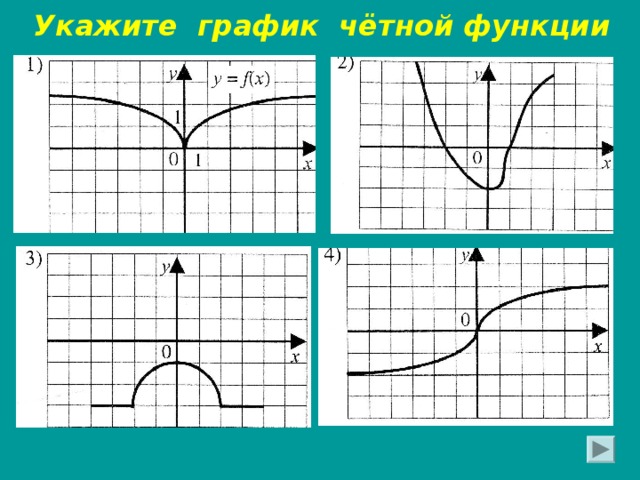
Укажите график чётной функции

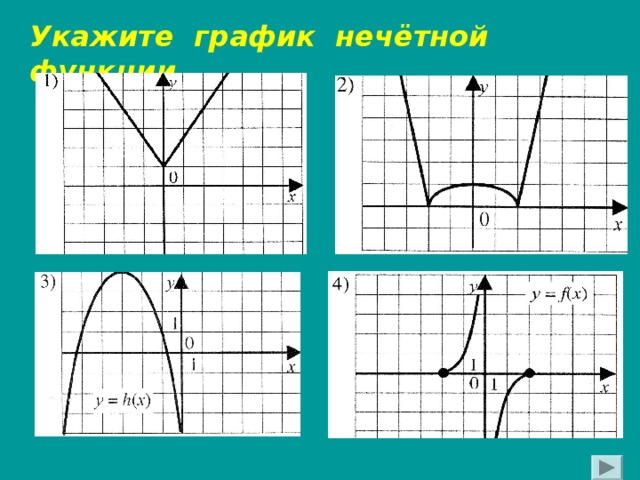
Укажите график нечётной функции

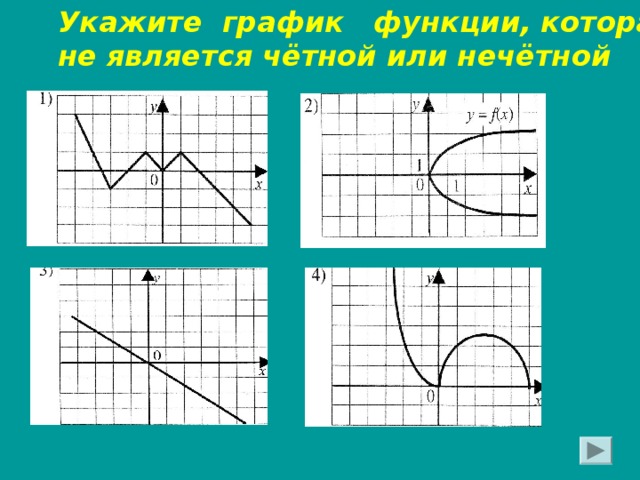
Укажите график функции, которая

не является чётной или нечётной

Ломаная АВС, где А ( 5; 1 ), В ( 3; 5 ), С ( 0; 0 ) –

часть графика некоторой функции f ( x ).

Область определения этой функции – промежуток [ -5; 5 ].

Постройте ее график, зная, что:

• f ( x ) – четная .

б) f ( x ) – нечетная.

Существуют функции, которые не обладают свойствами чётности или нечётности.

y = 2 x + 1

у

График в этом случае не обладает свойством симметрии

0

х

Спасибо за внимание!!!!