Свойства тригонометрических функции

Тригонометриялық функциялардың қасиеттері

• 1. Математика ақыл-ойды тәртіпке келтіреді.Сондықтан да оны оқу керек.(С.Ломоносов)
• 2. Математиканың өзіне тән тілі бар – ол формулалар. (С.Ковалевская)
• 3. Арифметика-математиканың, ал математика – барлық ғылымдардың патшасы .(К.Гаусс)
• 4. Поэзиядағыдай математиканың өзіне тән сұлулығы бар. (А.С.Пушкин)

-

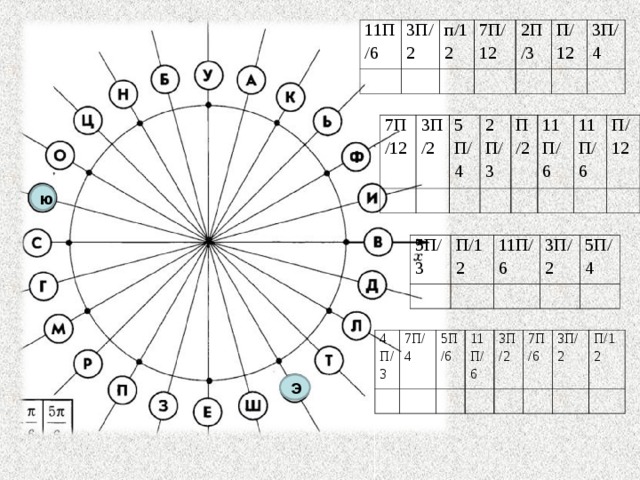
Градустық /радиандық/

өлшемде берілген бұрышты

радиандық/ градустық/

өлшемге қалай ауыстыруға болады?

11П/6

3П/2

п/12

7П/12

2П/3

П/12

3П/4

7П/12

3П/2

5П/4

2П/3

П/2

11П/6

11П/6

П/12

ю

5П/3

П/12

11П/6

3П/2

5П/4

4П/3

7П/4

5П/6

11П/6

3П/2

7П/6

3П/2

П/12

Э

Тригонометрия грек тілінен алынған тригонон-үшбұрыш,метрео-өлшеуіш.Тригонометрия үшбұрыштарды өлшеу жөніндегі ғылым.  Тригонометрия элементтерін адамзат ежелгі замандардан бастап, бұрыштарды өлшеу мұқтаждықтары барысында қолдана бастаған.  Ең алғашқы жүйелі тригонометриялық кестелерді К.Птолемей (біздің заманымызға дейінгі ІІғ)жасаған.Ол өз еңбектерінде 60-тық санақ жүйесін қолданып, шеңберді өзара тең 360 бөлікке бөліп қарастырған.Ал үнді ғалымдары есептеу жұмыстарында синус пен косинустың кестелерін құрастырған.

Синус сөзі латын тілінен аударғанда «дөңестік, доға»деген мағынаны білдіреді,ал косинус «толықтауыш» деген мағынаны білдіреді.Осы күнгі қолданып жүрген sin х және cos х белгілеулері 1739 жылы И.Бернуллидің Л.Эйлерге жазған хатында алғаш рет ұсынылған. Бұл белгілеулерді соңынан Л.Эйлер және өзгелер кеңінен қолдана бастады. Эйлер « tgx, ctgx, secx, cosecx » белгілеулерін енгізді.

Secx=1/cosx cosecx=1/sinx

Л.Эйлер (1707-1783)тригонометриялық функцияларды анықтауда тригонометриялық шеңберлерді қарастыру арқылы, бірнеше негізгі формулалар көмегімен өзге барлық формулаларды қорытып шығарады. 

Синустар мен косинустар қатарын И.Ньютон 1666 ж . Құрастырды.

0 , cos 0 І ширек Sin ІІ ширек Sin 0, tg 0 ІІІ ширек І V ширек Ctg 0, sin Cos " width="640"

бұрышы қай ширекке тиісті екенін бағыт арқылы

қосып көрсетіңдер / сәйкес жауаптарды байланыстырыңдар/

Sin 0 , cos 0

І ширек

Sin

ІІ ширек

Sin 0, tg 0

ІІІ ширек

І V ширек

Ctg 0, sin

Cos

І ширекте оң таңба қабылдайды.

ІІ ширекте оң таңба қабылдайды.

ІІІ ширекте оң таңба қабылдайды.

І V ширекте оң таңба қабылдайды.

І ширекте теріс таңба қабылдайды.

ІІ ширекте теріс таңба қабылдайды.

ІІІ ширекте теріс таңба қабылдайды.

І V ширекте теріс таңба қабылдайды.

А нүктесінің ординатасының абсциссасына қатынасын атайды .

А нүктесінің ординатасының радиусқа қатынасын атайды.

А нүктесінің абсциссасының ординатасына қатынасын атайды .

А нүктесінің абсциссасының радиусқа қатынасын атайды .

Жұп функция.

Тақ функция.

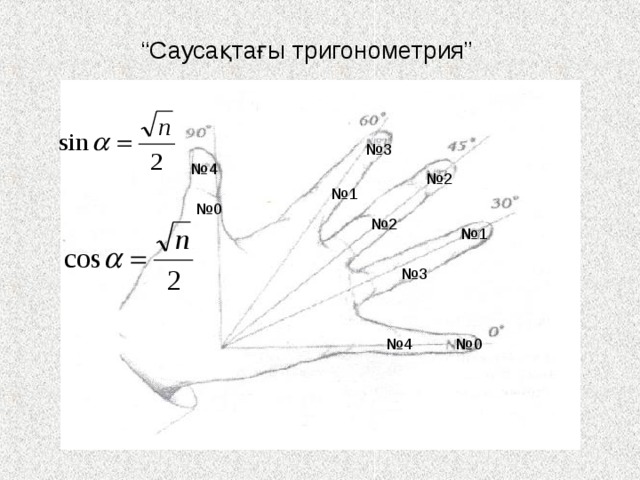
“ Саусақтағы тригонометрия”

№ 3

№ 4

№ 2

№ 1

№ 0

№ 2

№ 1

№ 3

№ 4

№ 0

Негізгі тригонометриялық теңбе- теңдіктерді жалғастырыңдар :

Өрнектерді ықшамдаңдар:

• қайталауды қажет етпейді бәрін түсіндім
• келесі сабақта осы тапсырма жайлы есіме

түсірсе екен

-қиын, сыныпта тағыда қайталап, ұқсас есеп

шығарғым келеді

Бұрыштың радиандық өлшемдері

Тригонометриялық функциялардың қасиеттері

Негізгі тригонометриялық теңбе-теңдіктерді қолдану

Саусақтағы тригонометрия